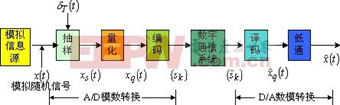
ADC采样原理
现状尽管国内有华为、紫光、中芯微等一定知名度的芯片企业,但与欧美等企业差距很大,尤其在ADC芯片上表现尤为显著。目前ADC的供应商主要有德州仪器、亚德诺等企业。中国是全球最主要的芯片需求方,但是国内能造出高精度ADC芯片的企业微乎其微,即便造出来性能与价格也跟不上市场节奏故市场占有率几乎为0。芯片千万种,ADC芯片就是最难造的之一。真实世界的模拟信号,例如温度、压力声音或者图像等需要转换成 更容易
现状
尽管国内有华为、紫光、中芯微等一定知名度的芯片企业,但与欧美等企业差距很大,尤其在ADC芯片上表现尤为显著。目前ADC的供应商主要有德州仪器、亚德诺等企业。中国是全球最主要的芯片需求方,但是国内能造出高精度ADC芯片的企业微乎其微,即便造出来性能与价格也跟不上市场节奏故市场占有率几乎为0。
芯片千万种,ADC芯片就是最难造的之一。真实世界的模拟信号,例如温度、压力声音或者图像等需要转换成 更容易存储、处理和发射的数字形式 。模/数转换器(ADC)就实现了这个功能,在实际应用中为了微型化,通常做成ADC芯片。
造芯片工艺精密,通常芯片单位为纳米级,而且种类繁多,一个通信基站就有上百颗芯片。基站发射回收信号,信号回收后首先要 滤波 ,然后还有芯片会将这种特别小的信号进行 放大 ;还有的芯片对其进行 解析 、 处理 ;然后是芯片负责 传输 、 分发 等等,每一步都要芯片来处理。
全球造出高精度ADC芯片不到十家,而且以美国企业为主。一块好的ADC芯片体现在 高精度 、 低功耗 、 转换效率 等指标上。
采样定理
又称奈奎斯特采样定理,即当采样频率fs 大于信号中最高频率fmax的2倍时,采样后的数字信号完整地保留了原始信号中的信息。在一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
1924 Nyquist(奈奎斯特)推导出理想低通信道的最高码元传输速率公式(传码率)。
1928 H.奈奎斯特推出采样定理,故称为奈奎斯特采样定理。
1933年,俄罗斯科捷利尼科夫首次用公式严格表述这一定理。
1948 信息论创始人 香农对这一定理加以明确地说明,并正式作为定理引用,故许多文献也称香农采样定理。
采样定理有很多表述形式,但最基本的是 时域采样定理 和 频域采样定理 。
1.1 时域
频带为F的连续信号f(t)可用一系列离散的采样值f(t1)、f(t1±Δt)、f(t1±2Δt)…来表示,只要这些采样点的时间间隔Δt ≤ 1/(2F),便可根据各采样值完全恢复原来的信号f(t)。这是时域采样定理的一种表达。
另一种表述方式是:当时间信号函数f(t)的最高频率分量为fM时,f(t)的值可由一系列采样间隔小于或等于1/(2fM)的采样值来确定,即采样点的重复频率f≥(2fM)。图为模拟信号和采样样本的示意图。
我的理解:一个时间上连续的函数或波形,这个波形的最高频率达到fM,现要想用一个离散的值去表示它,并且不丢失信息,那对这一组离散值的最低要求是:这组离散值相邻值之间的时间间隔Δt不能超过T = 1/(2fM)即有Δt ≤ 1/(2fM)。这么看来,在采样的时间上Δt有最大值,那么采样的频率上f=1/ Δt是由一个最小值,即f f≥(2fM)。
时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。
1.2 频域
对于时间上受限制的连续信号f(t)(即当│t│>T时,f(t)=0,这里T=T2-T1是信号的持续时间),若其频谱为F(ω),则可在频域上用一系列离散的采样值 来表示,只要这些采样点的频率间隔ω≦π/tm 。
1.3公式
理想低通信道的最高码元传输速度B=2W baud (其中W是带宽),理想信号的极限信息速率(信道容量)
C = B*log2N (bps)
1.4 结论
从信号处理角度看,采样定理描述了两个过程:采样与重建。采样是连续时间信号转换为离散时间信号,重建过程是对样本进行插值的过程,即从离散的样本x[n]中,用数学的方法确定连续的信号x(t)即原始信号。这一过程的精确度受量化误差的限制。
只要已知信号的最高频率fmax,采样定理给出了保证能完整重建此信号的最低采样频率。这一最低采样频率称为临界频率或奈奎斯特采样频率,用fN表示。反之,已知现有的采样频率,通过采样定理可知能保证重建信号的最大可采样信号频率。
同时也说明,被采样的信号必须是 带限的 ,即 信号中高于某一给定值的频率成分是0,或至少非常接近0,这样在重建信号中这些频率成分的影响可忽略不计。比如声音信号,人类的声音信号频率超过5Khz的成分非常非常小,因此其采样频率用10Khz就足够了。
采样率越高,稍后恢复出的波形就越接近原信号,但是对系统的要求就更高,转换电路必须具有更快的转换速度。
1.5 过采样(oversampling)
指以高于信号带宽2倍或其最高频率对其采样的过程。
欠采样
1.6 截止频率(Cutoff frequency)
指一个系统的输出信号能量开始大幅下降(在带阻滤波器中为大幅上升)的边界频率。
1.7 混叠
如果不满足采样定理条件,采样后的信号的频率就会重叠。即被采样信号中高于采样频率一半(fs/2)的那部分频率成分将被重建成低于fs/2信号。这种频谱的重叠导致的失真称为 混叠 。而重建出来的信号称为原信号的 混叠替身 ,因为这两个信号有同样的样本值。
避免混叠发生的方法:
- 提高采样频率 ;
- 引入低通滤波器 或提高低通滤波器的参数,该低通滤波器称为抗混叠滤波器。
1.8 抗混叠低通滤波器
当一个信号被采样时,必须满足采样定理以避免混叠。为满足采样定理要求,信号在进行减采样前,必须通过一个具有适当截止频率的低通滤波器。这中用于避免抗混叠的低通滤波器称为 抗混叠低通滤波器 。
1.9 信号的重构
任何信号都可以看做是不同频率的正弦(余弦)信号的叠加,因此如果知道所有组成这一信号的正(余弦)信号的幅值、频率和相角,就可以重构原信号。由于信号测量、分解及时频变换的过程中存在误差,因此不能100%地重构原信号,重构的信号只能保证原信号误差在容许范围内。
ADC
数字信号变成模拟信号会产生量化噪声,需要模拟低通滤波器滤除,但模拟低通滤波器并非直接滤除截止频率以外的信号、而是大幅减少截止频率以外的信号、同时小幅减少及影响截止频率以内的信号。若能提高低通滤波器的截至频率,则模拟低通滤波器对期待保留的频段(以音响系统为例,就是人耳听得到的20hz-20khz)的影响就会降低;过采样可以将量化噪声推往更高频率、让系统可以选用更高截止频率的低通滤波器,借此避免 混叠、改善分辨率以及降低噪声。
很多场合都需要有高速的A/D采样保证有效性和精度,如无线电、数字图像采集等,一般的测控系统也希望在精度上有所突破。AD转换器是实现数字化的选择,其发展从 Flash并型 ADC 、 SAR型ADC 、 积分型ADC ,但近年来发展的 Σ-Δ型 和 Pipeline ADC , 各有优缺点,满足不同场合。
2.ADC工作原理
模拟信号转化为数字信号一般经过:采样、保持、量化和编码。采样和保持是在 采样保持电路中完成 ,而量化与编码步骤则在 ADC 中完成。

2.1采样与保持
2.1.1采样
采样就是把随时间连续变化的模拟量转换为时间离散的 模拟量 。


其中传输门TG受采样信号S(t)的控制,在S(t)的脉宽τ期间,传输门导通,输出为输入信号v1(t),而在(Ts-τ)期间,传输们关闭,输出信号为0。
通过分析可以看到,取样信号S(t)的 频率愈高 ,所取得信号经低通滤波器后 愈能真实地复现输入信号。但带来的问题是数据量增大,为保证有合适的取样频率,它必须满足取样定理。
2.1.2 保持
将采样电路取得的模拟信号转化为数字信号都 需要一定的时间 (不能做到实时转换),为了给后续的量化编码过程提供一个稳定值,每次取得的模拟信号必须通过保持电路保持一段时间。通过一个电容器就可以存储输入的模拟电压。


- 电路由 输入放大器A1 与 输出放大器A2 、 保持电容CH
 和 开关驱动电路 组成。
和 开关驱动电路 组成。 - 电路中要求A1具有很高的输入阻抗, 以减少对输入信号源的影响 。
- 为使 保持阶段CH
 上所存电荷不易泄放 ,A2也应具有较高输入阻抗,A2还应具有低的输出阻抗,这样可以提高电路的带负载能力。一般还要求电路中AV1·AV2=1。
上所存电荷不易泄放 ,A2也应具有较高输入阻抗,A2还应具有低的输出阻抗,这样可以提高电路的带负载能力。一般还要求电路中AV1·AV2=1。
现结合图4来分 析取样-保持电路的工作原理。在t=t0时,开关S闭合,电容被迅速充电,由于AV1·AV2=1,因此v0=vI,在t0~t1时间间隔内是取样阶段。在t=t1时刻S断开。若A2的输入阻抗为无穷大、S为理想开关,这样可认为电容CH没有放电回路,其两端电压保持为v0不变,图中t1到t2的平坦段,就是保持阶段。
取样-保持电路以由多种型号的单片集成电路产品。如双极型工艺的有AD585、AD684;混合型工艺的有AD1154、SHC76等。
量化与编码
数字信号不仅在时间上是离散的,而且在幅值上也是不连续的。任何一个数字量的大小只能是某个规定的最小数量单位的整数倍。为将模拟信号转换为数字量,在A/D转换过程中,还必须将取样-保持电路的输出电压,按某种近似方式归化到相应的离散电平上,这一转化过程称为数值量化,简称量化。量化后的数值最后还需通过编码过程用一个代码表示出来。经编码后得到的代码就是A/D转换器输出的数字量。
量化过程中所取最小数量单位称为量化单位,用△表示。它是数字信号最低位为1时所对应的模拟量,即1LSB。
在量化过程中,由于取样电压不一定能被△整除,所以量化前后不可避免地存在误差,此误差称之为量化误差,用ε表示。量化误差属原理误差,它是无法消除的。A/D 转换器的位数越多,各离散电平之间的差值越小,量化误差越小。
量化过程常采用两种近似量化方式:只舍不入量化方式和四舍五入的量化方式。
1.只舍不入量化方式
以3位A/D转换器为例,设输入信号v1的变化范围为0~8V,采用只舍不入量化方式时,取△=1V,量化中不足量化单位部分舍弃,如数值在0~1V之间的模拟电压都当作0△,用二进制数000表示,而数值在1~2V之间的模拟电压都当作1△,用二进制数001表示……这种量化方式的最大误差为△。
2.四舍五入量化方式
如采用四舍五入量化方式,则取量化单位△=8V/15,量化过程将不足半个量化单位部分舍弃,对于等于或大于半个量化单位部分按一个量化单位处理。它将数值在0~8V/15之间的模拟电压都当作0△对待,用二进制000表示,而数值在8V/15~24V/15之间的模拟电压均当作1△,用二进制数001表示等。
3.比较
采用前一种只舍不入量化方式最大量化误差│εmax│=1LSB,而采用后一种有舍有入量化方式│εmax│=1LSB/2,后者量化误差比前者小,故为多数A/D转换器所采用。
随着集成电路的飞速发展,A/D转换器的新设计思想和制造技术层出不穷。为满足各种不同的检测及控制需要而设计的结构不同、性能各异的A/D转换器应运而生。
下面简单讲讲A/D转换器的基本原理和分类:
根据A/D转换器的原理可将A/D转换器分成两大类。一类是直接型A/D转换器,将输入的电压信号直接转换成数字代码,不经过中间任何变量;另一类是间接型A/D转换器,将输入的电压转变成某种中间变量(时间、频率、脉冲宽度等),然后再将这个中间量变成数字代码输出。
尽管A/D转换器的种类很多,但目前广泛应用的主要有三种类型:逐次逼近式A/D转换器、双积分式A/D转换器、V/F变换式A/D转换器。另外,近些年有一种新型的Σ-Δ型A/D转换器异军突起,在仪器中得到了广泛的应用。
逐次逼近式(SAR)A/D转换器(SAR)的基本原理是:将待转换的模拟输入信号与一个推测信号进行比较,根据二者大小决定增大还是减小输入信号,以便向模拟输入信号逼进。推测信号由D/A转换器的输出获得,当二者相等时,向D/A转换器输入的数字信号就对应的时模拟输入量的数字量。这种A/D转换器一般速度很快,但精度一般不高。常用的有ADC0801、ADC0802、AD570等。
双积分式A/D转换器的基本原理是:先对输入模拟电压进行固定时间的积分,然后转为对标准电压的反相积分,直至积分输入返回初始值,这两个积分时间的长短正比于二者的大小,进而可以得出对应模拟电压的数字量。这种A/D转换器的转换速度较慢,但精度较高。由双积分式发展为四重积分、五重积分等多种方式,在保证转换精度的前提下提高了转换速度。常用的有ICL7135、ICL7109等。
Σ-Δ型AD由积分器、比较器、1位D/A转换器和数字滤波器等组成。原理上近似于积分型,将输入电压转换成时间(脉冲宽度)信号,用数字滤波器处理后得到数字值。电路的数字部分基本上容易单片化,因此容易做到高分辨率。主要用于音频和测量。这种转换器的转换精度极高,达到16到24位的转换精度,价格低廉,弱点是转换速度比较慢,比较适合用于对检测精度要求很高但对速度要求不是太高的检验设备。常用的有AD7705、AD7714等。
V/F转换器是把电压信号转换成频率信号,由良好的精度和线性,而且电路简单,对环境适应能力强,价格低廉。适用于非快速的远距离信号的A/D转换过程。常用的有LM311、AD650等。
整改自:
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)