
MLA——一文通透DeepSeek V2中的多头潜在注意力MLA:改进MHA,从而压缩KV缓存,提高推理速度(含让任何LLM都能用上MLA的方法)
前言
成就本文有以下三个因素
- 24年5.17日,我在我司一课程「大模型与多模态论文100篇」里问道:大家希望我们还讲哪些论文
一学员朋友小栗说:幻方旗下公司深度求索于24年5.7日发布的deepseek-v2 - 24年5.24日,我司一课程「大模型项目开发线上营1」里的一学员朋友问我:校长最近开始搞deepseek了吗?刚看了论文,没搞懂MLA那块的cache是怎么算的,我总觉得他的效果应该类似MQA才对,但是反馈是挺好的
我当时回复他道:目前团队项目上的事情太多,然后近期在写那个KAN
确实还没来得及看这个deepseek,我近期看下 - 我们在继英文层面的论文翻译、审稿、对话、idea提炼之后(其中的审稿和翻译已于24年8月底上线七月官网 )
打算再整一下中文层面的「硕士论文修订助手(不限学科,CS和非CS的都涵盖)」,预计24年9月份上线七月官网
对于模型的选择,在闭源之外,在开源模型上 有两个选择,一个chatglm4,一个DeepSeek(后来实际上线时,一开始用的deepseek v2,后来改成了deepseek v3)
而搞DeepSeek之前——近几天,会先写一下它的论文解读(当然,因为DeepSeek-V2从DeepSeek LLM、DeepSeekMoE迭代而来,且用到了DeepSeekMath中的GRPO算法,故第一部分会先讲DeepSeek LLM、DeepSeekMoE、DeepSeekMath),故本文就来了,且DeepSeek也算证明了在国内也可以做出有效果、有影响力的创新
且一如既往做到——对于几乎每一个主题,都如本博客万千读者或七月学员所说的:“还是看校长的文章好理解”,而其中的关键之一是做好图、文、公式的一一对应,不一笔带过、不自以为然,本文亦如此
同时本文也见证了自己从技术人到产品人定位的过渡
- 23上半年 侧重原理,系统大量读paper,深挖原理
- 23下半年 侧重工程,和项目组不断优化各种工程问题
- 24上半年 侧重研究,横跨或综合多个领域(比如llm+机器人),继续各种抠paper
- 24下半年 侧重产品,把世界级前沿落地成产品 给用户使用,以发挥更大的价值和影响力(希望有机会早日达到世界级影响力)
第一部分 从DeepSeek LLM、DeepSeekMoE到DeepSeekMath
友情提醒,如不需要透彻深入理解,或者想直接看DeepSeek-V2的,可以直接跳到本文的第二部分,本文第二部分也是本文的最精华所在
当然,如果你就是想先从本第一部分 开始看则非常好,但里面的数学公式比较多,喜欢抠公式的可以细抠,不喜欢抠公式的则不用抠太细,不影响对DeepSeek-V2的整体理解
| 原标题 | 1.1 DeepSeek LLM的预训练与对齐 | 1.2 DeepSeekMoE的创新:细粒度专家分割与共享专家隔离 | 1.3 DeepSeek-Coder、DeepSeekMath及其提出的GRPO | |
| 提出时间 |
24年1.5日,量化巨头幻方旗下的杭州深度求索公司提出DeepSeek LLM,其对应的论文为《DeepSeek LLM: Scaling Open-Source Language Models with Longtermism》 |
24年1.11日,深度求索公司很快又提出了DeepSeekMoE,其对应的论文为《DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models》 |
24年1.25,深度求索公司又提出DeepSeek-Coder |
因为DeepSeek-V2涉及到了DeepSeekMath「其对应论文为 24年2月发表的《DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models》」中提出的群体相对策略优化——Group Relative Policy Optimization(简称GRPO) |
| 改动 | 本1.1节后已独立成文,详见下文的「3.1节DeepSeek LLM的预训练与对齐」 | 因为MoE架构的重要性,本1.2节后已独立成文,详见下文的「3.2节DeepSeekMoE的创新:细粒度专家分割与共享专家隔离」 | 对应的论文为《DeepSeek-Coder: When the Large Language Model Meets Programming -- The Rise of Code Intelligence》 | 后本1.3节已独立成文,详见下文 |
| 对应的新文章 | 一文速览DeepSeekMoE及相关MoE大模型:从Mixtral 8x7B到DeepSeekMoE(含DeepSeek LLM的简介)、Qwen2.5-Max | 一文速览DeepSeekMoE及相关MoE大模型:从Mixtral 8x7B到DeepSeekMoE(含DeepSeek LLM的简介)、Qwen2.5-Max | 一文速览DeepSeekMath及GRPO:通俗理解群体相对策略优化GRPO(含DeepSeek-Coder的简介) | |
第二部分 DeepSeek-V2:提出多头潜在注意力MLA且改进MoE
DeepSeek-V2属于DeepSeek的第二代版本,参数规模虽然达到了庞大的236B,但由于其MoE的结构,使得其中每个token激活仅21B的参数,且支持128K的上下文(It is equipped with a total of 236B parameters, of which 21B are activated for each token, and supports a context length of 128K tokens)

其对应论文为《DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model》,发布于24年5.7日
- 他们首先在完整的预训练语料库上预训练DeepSeek-V2
- 然后,收集了150万个对话会话,涵盖了数学、代码、写作、推理、安全等各个领域,以对DeepSeek-V2 Chat(SFT)进行监督微调(SFT)
- 最后,他们遵循DeepSeekMath的方法,采用组相对策略优化(GRPO)进一步使模型与人类偏好对齐,并生成DeepSeek-V2 Chat(RL)
DeepSeek-V2主要有两大创新点,其在Transformer架构「一个注意力模块和一个前馈网络(FFN),如对transformer还不够熟练,请看此文:Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT」的基础上
- 改造注意力模块
其通过创造性的提出多头潜在注意力:Multi-head Latent Attention(简称MLA),替代传统多头注意力(Multi Head Attention)
具体而言,MLA利用低秩键值联合压缩(low-rank key-value joint compression)来降低推理时的KV Cache开销——相当于low-rank joint compression for keys and values to reduce KV cache,且性能不输于MHA(论文中说的是性能比MHA还更好)
我个人认为,MLA本质上也是受到了LoRA和Stable Diffusion的启发「前者详见此文《LLM高效参数微调方法:从Prefix Tuning、Prompt Tuning、P-Tuning V1/V2到LoRA、QLoRA(含对模型量化的解释)》,后者详见此文《AI绘画原理解析:从CLIP、BLIP到DALLE、DALLE 2、DALLE 3、Stable Diffusion(含ControlNet详解)》」
所以MLA 是多头潜在注意力,在多头注意力上 加上了低秩KV压缩 - 改造FFN
其把FFN的结构改成DeepseekMoE——是对传统MoE结构的改进(下图各种结构、表示很多,初看难以一看就懂,没事,下文会逐一详解,任何一个符号都不会放过——最后,反复琢磨之后,你也可以和我一样:脱离本文,手绘下图、手推下图背后的公式)
值得一提的是,他们还一块发布了 DeepSeek-V2-Lite,相当于配备 MLA 和 DeepSeekMoE 的较小模型,它总共有15.7B参数,其中每个token激活2.4B参数(we also release DeepSeek-V2-Lite, a smaller model equipped with MLA and DeepSeekMoE, for the open-source community. It has a total of 15.7B parameters, where 2.4B are activated for each token)
- DeepSeek-V2-Lite 有 27 层,隐藏维度为 2048。 它还采用 MLA,并具有 16 个注意力头,每个头的维度为 128
其 KV 压缩维度为 512,但与 DeepSeek-V2 略有不同,它不压缩查询
对于解耦查询和键,每头维度为 64 - DeepSeek-V2-Lite 还采用 DeepSeekMoE,除了第一层外,所有前馈神经网络 (FFNs) 都被 MoE 层替换
每个 MoE 层由 2 个共享专家和 64 个路由专家组成,每个专家的中间隐藏维度为 1408。 在这些路由专家中,每个token将激活6个专家 - DeepSeek-V2-Lite 也在与 DeepSeek-V2 相同的预训练语料库上从头开始训练,该语料库未被任何 SFT 数据污染
它使用 AdamW 优化器,超参数设置为 𝛽1 = 0.9, 𝛽2 =0.95,权重衰减 =0.1
学习率使用预热和阶梯衰减策略进行调度
最初,在前2000步期间,学习率从0线性增加到最大值
随后,在训练了大约80%的tokens后,学习率乘以0.316,并在训练了大约90%的tokens后再次乘以0.316
最大学习率设置为4.2 × 10−4,梯度裁剪范数设置为1.0
没有采用批量大小调度策略,而是以恒定的批量大小4608个序列进行训练
在预训练期间,将最大序列长度设置为4K,并在5.7T tokens上训练DeepSeek-V2-Lite
2.1 DeepSeek-V2提出MLA的背景与作用
2.1.1 KV Cache所导致的显存消耗大,需要尽可能降低
众所周知,KV Cache是大模型标配的推理加速功能——也是推理过程中,显存资源巨大开销的元凶之一。如下图所示,在模型推理时,KV Cache在显存占用量可达30%以上

目前大部分针对KV Cache的优化工作
- 比如著名的vLLM「这是其介绍页面、这是其对应的GitHub、其论文则为:Efficient Memory Management for Large Language Model Serving with PagedAttention,当然了,我也写了一篇专门介绍vLLM的博客,详见《一文通透vLLM与其核心技术PagedAttention:减少KV Cache碎片、提高GPU显存利用率(推理加速利器)》」,其基于paged Attention,最大限度地利用碎片化显存空间,从而提升了空间利用率
- 再比如GQA、MQA
GQA是query数不变,但多个query(比如2个)组成一个group以共享一个key value
MQA则query也不变,但所有query(比如8个)共享一个key、一个value
至于更多,详见此文:一文通透各种注意力:从多头注意力MHA到分组查询注意力GQA、多查询注意力MQA
这些方案的问题是什么呢?在于
- 第一类方案并没有从根本上改变KV Cache占用空间巨大的问题
- 而第二类方案中的MQA虽然较大降低了KV cache计算量,但性能相比MHA下降太多了
至于第二类方案中的GQA则取了个折中:不好的是缓存下降的不够多、好的是相比MHA性能没有下降太多,毕竟我们追求的是缓存下降、性能不降
那KV Cache到底是什呢
- 对此,我们先来回顾下transformer当中的注意力计算公式
- GPT预测下一个token时,其只能看到待预测token之前的所有token,故在最终生成
整个序列的过程中,会涉及到如下计算过程
- 然后把上面的softmax结果和对应的V值一相乘,便可得到
可以很明显的看到,上述计算过程中,有不少的重复计算,比如
、
、
上面这句话值得反复品味三遍!
如果序列长度越长,类似这样的重复计算会越多,从而势必将白白消耗那么大的显存,所以才说需要降低这种
重复计算
2.1.2 Multi-head Latent Attent:致力于在推理中降低
MLA是对传统多头注意力做的改进,其目的有两个:首先是,降低推理过程中的KV Cache资源开销,其次,缓解MQA、MGA对性能的损耗
如上文所说,KV Cache中,提到每一步都需要将K和V缓存下来
具体而言,对于单个Attention Block块中的多头注意力——举个例子,假设
- 输入embedding的维度为
,比如512
- 然后有
个头,比如8个头
- 每个头——
和
的维度为
,比如64
为注意力层中第
个token的输入,比如上图中的
——Thinking中的第五个token 是
- transformer的层数为
接下来
- 首先,标准的MHA会通过三个矩阵
分别生成
,即
相当于 - 然后,
将被切分成
个头用于多头注意力计算
其中分别表示第
个注意力头的查询、键和值
表示输出投影矩阵
- 最终,在推理过程中,需要缓存所有的键和值以加速推理,因此MHA需要为每个token缓存的参数量为
(注意,是针对每个token,总之,如论文中所说,During inference, all keys and values need to be cached to accelerate inference, so MHA needs to cache
elements for each token)
因此,MLA致力于在推理中降低,具体而言,其不直接减少cache数量,而是类似Lora微调方法

- 对Key和Value进行了一个低秩联合压缩(即Low-Rank Key-Value Joint Compression,通过低秩转换为一个压缩的KV,使得存储的KV的维度显著减小)

- 如上图所示(在MHA GQA中大量存在于keys values中的KV缓存——带阴影表示,到了MLA中时,只有一小部分的被压缩Compressed的Latent KV了)
那,MLA具体如何做压缩呢,详看下节
2.2 详解MLA的两个部分:一部分做压缩、一部分做RoPE编码
DeepSeek通过对Query和Key进行拆分为和
,其中一部分做压缩
、一部分做RoPE编码
「R可以理解为RoPE的标识符」

2.2.1 MLA对Q K V的压缩:先对KV联合压缩后升维,再对Q压缩后升维
2.2.1.1 先对KV联合压缩(Low-Rank Key-Value Joint Compression)、后升维
首先,对于上图右下角的、
、

三个变量、
、
分别通过如下三个公式计算得来
可以看到针对KV先一块降维(公式表示时用表示降维),再K、V各自升维(公式表示用
表示升维),具体而言
- 先针对KV联合压缩以降维,降维到
(即指上面的第一个公式)
对于上述第一个公式,其中的
是对key和value压缩后的潜在向量
对于
其维度表示KV被压缩后的维度——有意思的是很快下文会讲到deepseek v2中
被设置为
且远小于到头key和value的原始维度
「 上文有说,输入embedding的维度为比如512,然后有
个头 比如8个头(不过,deepseek v2中设置的128个头)
每个头——和
的维度为
比如64(不过,deepseek v2中头的维度设置的128) 」
具体如何被压缩的呢?
很简单,其通过一个降维映射矩阵和模型输入
相乘得到
- 再对K、V分别升维到以还原 (即指上面的第二、第三公式)
至于上述的第二公式、第三公式
怎么个具体计算过程呢?
过程也很简单
在于通过第一个公式得到后,具体的key和value由两个对应的升维矩阵
还原——见下图的最右下角,就得到了上面的第二、第三公式拉
且在推理的过程中
1) 只需要缓存每一步的,然后再计算还原回原始的K和V即可,由于
的维度远小于K、V,因此每一步token的推理产生的缓存由之前的
,变成
2) 由于可以吸收到
中,而
可以吸收到
中,如此甚至不需要计算注意力的键和值(即如论文中所说,during inference, since 𝑊𝑈𝐾 can be absorbed into 𝑊𝑄, and 𝑊𝑈𝑉 can be absorbedinto 𝑊𝑂, we even do not need to compute keys and values out for attention)
注,为方便大家更好的理解
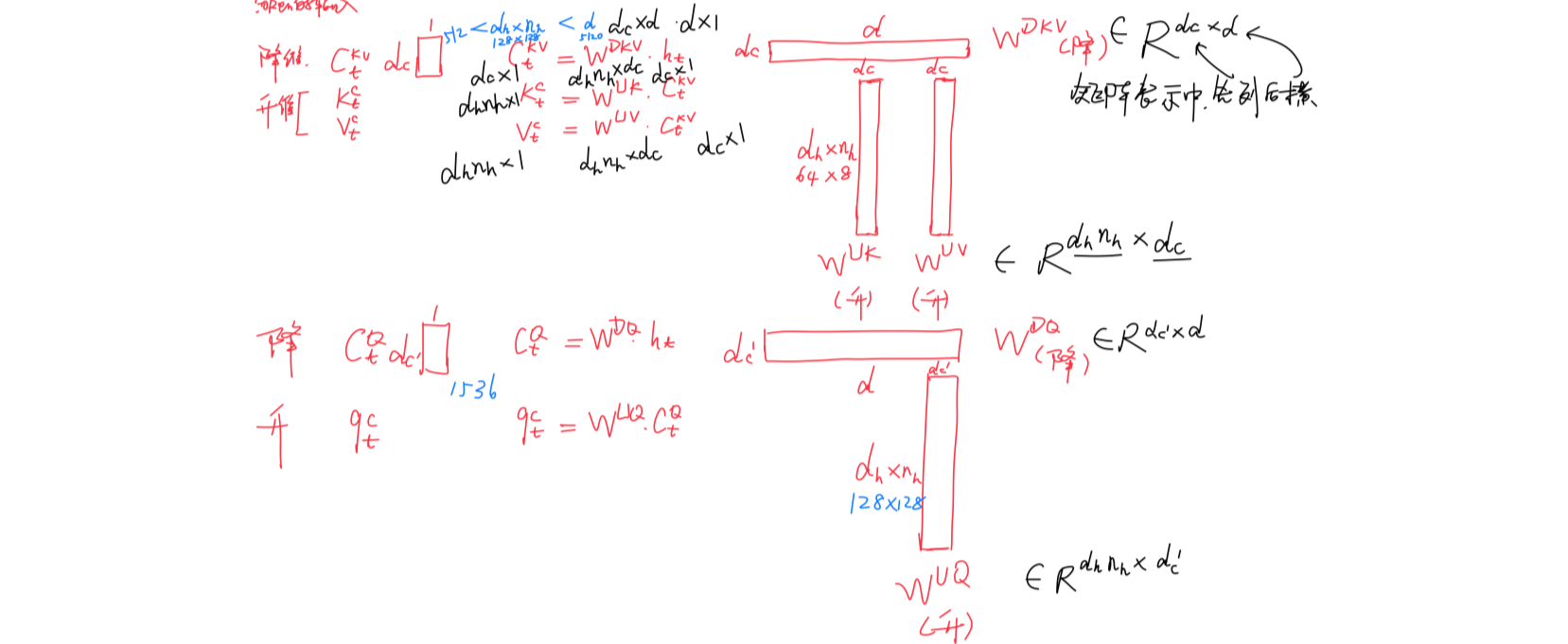
- 我于24年8月27日晚上特地花了个把小时(反复琢磨、反复修改),用手头的iPad Pro + apple pencil画了下上述过程,以方便大家一目了然的对比前后维度的变化(至于下图底部中“除了
之外”的怎么回事,不急,下文很快会逐一阐述)
如下图所示(后被证实画的有问题)
- 后在25年3.25日,我司七月在线的大模型线上营学员兼deepseek实战营学员朋友owl提醒,我上面的画法有问题,仔细一看,还真是,不单他指出的地方有问题「比如对于一个4×3的矩阵而言,则代表4行 3列,相当于其中高度为4 宽度为3」,且他没指出的一些地方也有问题,故修正如下
可以对比下V2论文中的示意图
2.2.1.2 再对Q压缩降维、后升维
其次,对于上图左下角的、

- 之前提到KV Cache中,Q的作用只发生在当下(预测下一个token时,其只能看到待预测token之前的所有token),但是在模型训练的过程中,每个输入的token会通过多头注意力机制生成对应的query、key和value
这些中间数据的维度往往非常高,因此占用的内存量也相应很大 - 所以论文中也提到为了降低训练过程中的激活内存activation memory,DeepSeek-V2还对queries进行低秩压缩——即便这并不能降低KV Cache,而其对Q的压缩方式和K、V一致,依然是先降维再升维
其中
是查询向量的压缩潜在向量(the compressed latent vector for queries)
表示查询向量压缩后的维度(为了区别上面的
,所以用
表示)
- 而
、
则分别表示查询向量的下投影矩阵、上投影矩阵(相当于还是先降维再升维)
2.2.2 MLA对query和key的RoPE编码
先说结论,如下图红框所示,需要对做RoPE编码,并对其中的Key位置编码的部分进行Cache
![]() ,从而在推理时不需要对Key进行位置编码的计算,提高了推理效率
,从而在推理时不需要对Key进行位置编码的计算,提高了推理效率

再说原因,即选择对做RoPE编码的背后有何深意呢?且听我july慢慢道来
首先,在RoPE的实现中,如果要让Q、K带上位置信息,会分别乘以相应的位置编码矩阵
如果计算QK时,自然就变成了
对于上面这个公式,有两个小细节值得一提
- 正确的就是
假设 Q 和 K 是列向量(维度 d×1)
其维度为
而非
其维度为
有同学可能问,为何不是Q乘以K的转置了,原因在于上RoPE与标准注意力计算顺序是各自独立的
- 根据旋转矩阵的正交性,
可以转化为

经典自注意力 RoPE 仅依赖 Q 和 K 的相似性 额外编码位置差 n−m 绝对位置需显式嵌入 相对位置通过旋转矩阵隐式编码
通过上一节可知,DeepSeek-V2对Q和K都进行了压缩(如下图 带着蓝色下划线的):、
则整个过程变成
其中的和
——如上节所述,分别是用于从低秩表示恢复到原始维度的解压缩矩阵(说白了,就是升维的)
然问题是
- 由于低秩表示已经是压缩了的状态,故直接在
和
上应用
和
,不等价于在完整的Q和K上应用位置编码(因为压缩操作可能已经丢失了某些信息,使得位置编码不能直接和有效地反映原始Q和K的位置关系)
换言之,RoPE与低秩KV压缩不兼容——RoPE is incompatible with low-rank KV compression
咋个具体不兼容法呢,具体来说,RoPE 对键和查询
都是位置敏感的。如果我们将RoPE 应用于键
,
,在方程
中将与一个位置敏感的RoPE 矩阵耦合
To be specific, RoPE is position-sensitive for both keys and queries. If we applyRoPE for the keys k𝐶𝑡, 𝑊𝑈𝐾in Equation 10 will be coupled with a position-sensitive RoPE matrix
这样一来,
在推理过程中就不能再被吸收到
中
「至于如何理解absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄, and 𝑊𝑈𝑉 into 𝑊𝑂,下文会提到,比如前者absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄
,此外,这里应该是
,而非论文原文中的
」
因为与当前生成的token相关的RoPE 矩阵将位于和
之间,即如上计算得到的
而矩阵乘法不遵循交换律
In this way, 𝑊𝑈𝐾 cannot be absorbed into 𝑊𝑄——此处应该为any more during inference, since a RoPE matrixrelated to the currently generating token will lie between 𝑊𝑄 and 𝑊𝑈𝐾 and matrix multiplication does not obey a commutative law
因此,必须在推理过程中重新计算所有前缀token的键,如此 这将显著阻碍推理效率
As a result, we must recompute the keys for all the prefixtokens during inference, which will significantly hinder the inference efficiency - 为了解决这问题,Deepseek-V2设计了两个pe结尾的变量——
、
(如论文中所说,we propose the decoupled RoPE strategy that uses additional multi-head queries q𝑅𝑡,𝑖 ∈ R𝑑𝑅ℎ and a shared key k𝑅𝑡 ∈ R𝑑𝑅ℎ to carry RoPE, where
denotes the per-head dimension of the decoupled queries and key,即表示解耦查询和键的每头维度)——亦即如下图红框里的两个变量
以用于储存旋转位置编码的信息,从而将信息存储和旋转编码解耦开
其中,、
分别是用于生成解耦查询和键的矩阵,如下图的最右下角所示
且顺带总结一下
首先,因为做了压缩
故不能直接在上应用
从而也就不能
故额外设计两个变量——如上图左下角所示
使得有 - 可能如果没有再三强调,有的宝子们便不太注意
故,我july再提一下上面这句话中“将信息存储和旋转编码解耦开”隐藏的一个细节,即如下图所示
对
进行RoPE编码时,它是直接从input hidden
上来的
「 相当于此时的不搞上一节所述的先降维、后升维那一套
」
所以才有的对
进行RoPE编码时,它取自的latent
「相当于此时的
做了潜在压缩
,但没做升维
」
所以才有的
请注意上面这两句话的含金量,这点几乎没有文章会给你特地强调出来的,虽然它本身就是个事实性的存在
压缩完、且RoPE编码完之后,最后将这4个变量——、
、
、
,分别拼接起来,形成
- 带信息压缩的Q——
、K——
- 带位置信息的Q——
、K——

以进行最后的计算
- 其中蓝色框中的向量
、
需要缓存以进行生成。 在推理过程中,the naive formula需要从
中恢复
和
以进行注意力计算
- 幸运的是,由于矩阵乘法的结合律,可以将
吸收到
中,并将
吸收到
中。 因此,不需要为每个查询计算键和值。 通过这种优化,避免了在推理过程中重新计算
和
的计算开销
注意了,「将
吸收到
中,并将
吸收到
」这点到底如何理解呢?一般的文章很少会详尽细致的阐述出来
我在另一篇文章中费了比较大的篇幅进行深入阐述,详见此文《MLA实现及其推理上的十倍提速——逐行解读DeepSeek V2中多头潜在注意力MLA的源码(图、公式、代码逐一对应)》的第二部分 MLA推理层面的改进:通过矩阵吸收十倍提速 MLA 算子,比如针对前者absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄,有

最终,单个Token产生的缓存包含了两个部分,即

其中,如上文说过的
- 有
个头,每个头——比如
和
向量的头维度为
,
表示为transformer的层数
表示为GQA中的组数
、
分别表示MLA中的KV压缩维度、解耦查询和键的the per-head dimension
在DeepSeek-V2中,被设置为
——512 = 4 × 128,
被设置为
——64 = 128/2,这三者之间的对应关系可以从下图中蓝色字体所标注出来的维度大小一目了然

因此,它的KV缓存等于只有2.25组的GQA,但其性能强于MHA
至于MLA的代码实现,详见上面提到过的此文《MLA实现及其推理上的十倍提速——逐行解读DeepSeek V2中多头潜在注意力MLA的源码(图、公式、代码逐一对应)》
2.3 DeepSeekMoE:以经济成本训练强大的模型
2.3.1 基本架构与Device-Limited Routing
由于在上文的1.3节,详细的介绍了DeepSeekMoE(包括细粒度专家分割和共享专家隔离),故本节描述从简
DeepSeekMoE有两个关键理念:
- 将专家细分为更细的粒度以实现更高的专家专业化和更准确的知识获取
- 隔离一些共享专家以减轻路由专家之间的知识冗余
最终,在激活和总专家参数数量相同的情况下,DeepSeekMoE 可以大幅超越传统的 MoE 架构

设为第
个标记的 FFN 输入,我们计算 FFN 输出
如下:
其中
和
分别表示共享专家和路由专家的数量
和
分别表示第
个共享专家和第
个路由专家
表示激活的路由专家数量
是第
个专家的门控值
是token到专家的亲和度
是这一层中第
个路由专家的质心
- 而
表示由计算出的第
个token和所有路由专家的亲和度得分中最高的
个得分组成的集合
对于DeepSeek-V2,除了简单的top-K路由专家选择外,其还确保每个token的目标专家最多分布在 𝑀个设备上。 具体来说,对于每个token,我们首先选择 𝑀个设备,这些设备中有专家具有最高的亲和分数
然后,在这些 𝑀个设备上的专家中进行top-K选择。 在实践中,我们发现当 𝑀 ⩾3 时,设备限制路由可以实现与不受限制的 top-K 路由大致一致的良好性能
2.3.2 负载均衡的辅助损失(Auxiliary Loss for Load Balance)
首先,不平衡的负载会增加路由崩溃的风险,防止某些专家得到充分的训练和利用。 其次,当采用专家并行时,不平衡的负载会降低计算效率
故在 DeepSeek-V2 的训练过程中,设计了三种辅助损失,分别用于控制专家级负载均衡、设备级负载均衡
和通信均衡
- 专家级均衡损失
- 设备级平衡损失
- 通信平衡损失
此外,虽然平衡损失旨在鼓励负载平衡,但需要承认它们不能保证严格的负载平衡
为了进一步减轻由于负载不平衡导致的计算浪费,他们在训练期间引入了设备级的Token-Dropping策略
- 这种方法首先计算每个设备的平均计算预算,这意味着每个设备的容量因子相当于1.0
- 然后,受Riquelme等人的启发,在每个设备上丢弃具有最低亲和力分数的token,直到达到计算预算
- 此外,确保大约10%的训练序列中的token永远不会被丢弃。 通过这种方式,可以根据效率要求灵活决定在推理过程中是否丢弃标记,并始终确保训练和推理之间的一致性
2.4(选读) MHA2MLA:MHA到MLA的丝滑迁移,让任何LLM都能用上MLA
通过上文对MLA的介绍,可知,MLA确实压缩了KV缓存,降低了KV缓存的显存消耗(正因为在推理过程中显著减少了KV缓存,从而提高了推理效率)

然可能有的同学便疑问说,既然MLA这么有用,在降低KV缓存的显存消耗上,比MQA、GQA都更有效,那如果某个LLM的注意力不换成MQA/GQA的话,那想换成MLA,怎么换呢?——即原本为 MHA 精心训练的大语言模型是否可以被适配以实现 MLA 推理?
- 由于MHA 和 MLA 之间固有的架构差异,使得零样本迁移变得不切实际,而从头开始的预训练的高昂成本使得这种转变在现有研究中既具有技术挑战性又未被充分探索
- 为填补这一空白,来自复旦 NLP 实验室、华东师大、上海 AI Lab、海康威视的研究者们联合提出 MHA2MLA 框架
其对应的论文为《Towards Economical Inference: Enabling DeepSeek's Multi-Head Latent Attention in Any Transformer-based LLMs》
其对应的GitHub为:JT-Ushio/MHA2MLA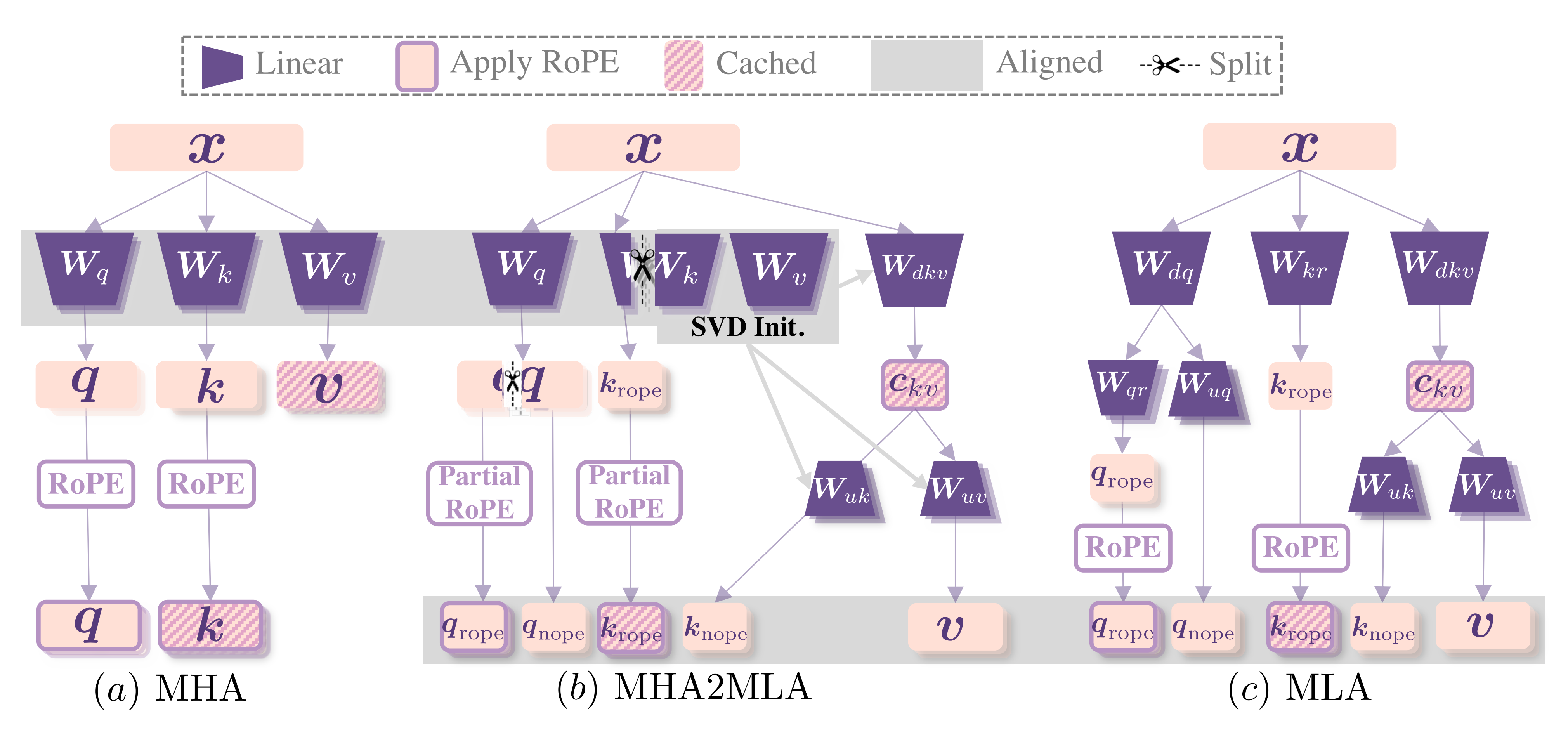
MHA2MLA通过部分旋转位置嵌入(Partial-RoPE)和键值联合表示低秩近似(Low-rank Approximation)两个关键步骤,成功将任意 MHA/GQA 架构迁移到 MLA
且该框架最大限度地重用了预训练的 MHA 网络的参数,同时使 KV 缓存存储和推理过程与MLA 的范式对齐
具体而言
- V2为了兼顾推理加速和RoPE,其解决方案是在保留部分维度的PE的同时压缩其他维度,这需要在MHA中策略性地移除RoPE维度(将其转化为NoPE)以实现MLA对齐
尽管更高的移除比率能提高压缩效率,但也会加剧性能的退化,形成效率与能力之间的权衡 - 但作者的工作可以将完整RoPE转换为部分RoPE。MLA通过将键和值投影到低秩潜在表示空间(存储在KV缓存中)来减少内存占用
MHA2MLA还可以对去除RoPE(NoPE维度)的值K和键V应用低秩近似
通过对预训练参数矩阵Wk和Wv对应的NoPE子空间进行奇异值分解(SVD),作者将这些组件压缩到潜在空间中,相当于部分Wk和Wv 做压缩得到
,同时最大化保留原始模型学习到的知识
一言以蔽之,在MHA的基础上
- 对于下图c所示的MLA不是对三个权重矩阵
、
、
简单的降维 去分别得到
、
、
,而是
对于q而言,先对降维得到降维矩阵
,然后
再一方面通过旋转矩阵
赋予被降维的q位置信息,得到
且二方面再对q通过
升维,得到

对于k和v而言,MLA的做法是一方面,通过
赋予k位置信息,得到
二方面,通过降维矩阵
对kv做联合降维得到
,之后再分别通过升维矩阵
、
对k、v升维
- 而对于上图b所示的MHA2MLA怎么做呢,其先保留三个矩阵
、
、
对于q而言,通过Wq矩阵得到q之后,拆解q,一部分q保留位置信息,得到,一部分没有位置信息,得到
对于k而言,最开始便把拆分成两个部分
一部分带位置信息的
,与k做点积得到
一部分没有位置信息的
与
合并且降维成
,然后再通过降维矩阵
对kv做联合降维得到
,之后再分别通过升维矩阵
、
对k、v升维
// 待更
第三部分 DeepSeek-V2的预训练与对齐
3.1 预训练(含数据构建与参数设置)、长度扩展、训练和推理效率
为提高其性能,他们构建了一个高质量的多源预训练语料库,包括8.1T的token,与DeepSeek 67B使用的语料库相比,该语料库的数据量有所增加,特别是中文数据,并且数据质量更高
且其采用与DeepSeek 67B相同的分词器,该分词器基于字节级字节对编码(BBPE)算法构建,词汇量为100K,其分词预训练语料库包含8.1T个token,其中中文token比英文标记多约12%
3.1.1 模型超参数
对于模型超参数,将Transformer层数设置为60,隐藏维度设置为5120——即。 所有可学习参数均以标准差0.006随机初始化
在MLA中
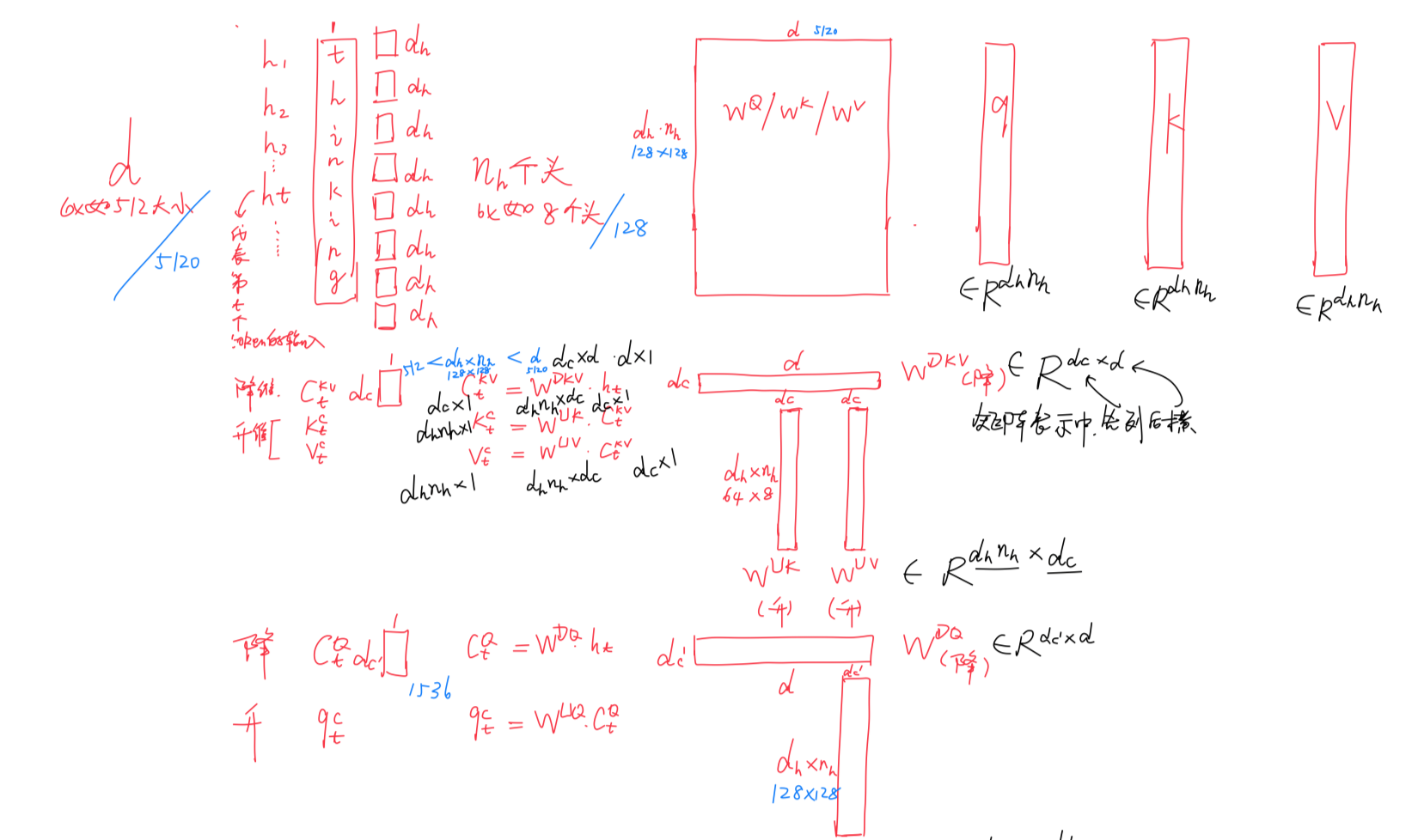
- 将注意力头的数量
设置为128
- 每头维度
设置为128
- KV压缩维度
设置为512「可以看出
」,其实也远远小于
查询压缩维度设置为1536——依然远小于
对于解耦查询和键,设置每头维度为64
上述3个数据的设置,其实也刚好呼应了上文2.2节最后说的
“在DeepSeek-V2中,被设置为
,
被设置为
”
在DeepSeekMoE中,按照Dai等人的做法
- 将除第一层外的所有前馈神经网络替换为专家混合层
每个专家混合层由2个共享专家和160个路由专家组成,每个专家的中间隐藏维度为1536 - 在这些路由专家中,每个token将激活6个专家
此外,低秩压缩和细粒度专家分割将影响层的输出规模 - 因此,在实践中,在压缩的潜在向量之后使用额外的RMS Norm层,并在宽度瓶颈处(即压缩的潜在向量和路由专家的中间隐藏状态)乘以额外的缩放因子,以确保训练的稳定性
在这种配置下,DeepSeek-V2总参数量为236B,其中每个token激活21B
3.1.2 训练超参数
以下是论文中所述的训练超参数设置
- 使用AdamW优化器(Loshchilov和Hutter,2017),超参数设置为 𝛽1 = 0.9, 𝛽2 =0.95,权重衰减 =0.1
- 学习率使用预热和阶梯衰减策略进行调度(DeepSeek-AI,2024)
最初,学习率在前2K步期间从0线性增加到最大值。
随后,在训练约60%的token后,学习率乘以0.316,并在训练约90%的token后再次乘以0.316
其中,最大学习率设置为2.4 × 10−4,梯度裁剪范数设置为1.0 - 还使用批量大小调度策略,在前225B token的训练中,批量大小从2304逐渐增加到9216,然后在剩余的训练中保持9216
- 将最大序列长度设置为4K,并在8.1T个tokens上训练DeepSeek-V2
- 利用流水线并行技术在不同设备上部署模型的不同层,对于每一层,路由的专家将均匀部署在8个设备上 (𝐷 =8)
至于设备限制路由,每个token最多会被发送到3个设备上 (𝑀 =3)。 关于平衡损失,我们将 𝛼1设置为0.003, 𝛼2设置为0.05, 𝛼3设置为0.02 - 在训练期间采用Token-Dropping策略以加速,但在评估时不丢弃任何token
此外,DeepSeek-V2基于HAI-LLM框架(High-flyer, 2023)进行训练,这是高效且轻量的训练框架
- 它采用了16路零气泡流水线并行(Qi等,2023),8路专家并行(Lepikhin等,2021),以及ZeRO-1数据并行(Rajbhandari等,2020)
- 鉴于DeepSeek-V2激活的参数相对较少,并且部分操作符会重新计算以节省激活内存,因此可以在不需要张量并行的情况下进行训练,从而减少通信开销
- 此外,为了进一步提高训练效率,我们将共享专家的计算与专家并行的全对全通信重叠
- 且还为通信、路由算法和融合定制了更快的CUDA内核
以及还基于改进版的 FlashAttention-2 (Dao, 2023) 进行了优化
最终,他们在配备 NVIDIA H800 GPU 的集群上进行所有实验。H800 集群中的每个节点包含 8 个GPU,这些 GPU 在节点内使用 NVLink 和 NVSwitch 连接。 在节点之间,使用 InfiniBand 互连来促进通信
3.1.3 长上下文扩展
在 DeepSeek-V2 的初始预训练之后,他们采用 YaRN「关于YaRN,详见此文《大模型长度扩展综述:从直接外推ALiBi、插值PI、NTK-aware插值(对此介绍最详)、YaRN到S2-Attention》的第四部分」将默认上下文窗口长度从 4K 扩展到 128K
- YaRN 专门应用于解耦的共享key
,因为它负责携带 RoPE (Su et al.,2024)
YaRN was specifically applied to the decoupled shared key k𝑅𝑡 as it is responsible for carrying RoPE - 对于 YaRN,将比例scale
设置为 40,
设置为 1,
设置为 32,并将目标最大上下文长度设置为 160K
另由于 DeepSeek-V2独特的注意力机制——MLA,与原始 YaRN 略有不同,故调整了长度缩放因子以调节注意力熵。 因子计算为
,旨在最小化困惑度
且另外训练了模型 1000 步,序列长度为 32K,批量大小为 576 个序列。 尽管训练仅在32K的序列长度下进行,但在128K的上下文长度下评估时,该模型仍表现出强大的性能
如下图所示,“大海捞针”(NIAH)测试的结果表明,DeepSeek-V2在所有上下文窗口长度(最长至128K)上表现良好

3.1.4 训练和推理效率
如论文中所说
在训练成本上
- 由于 DeepSeek-V2 对每个 token 激活的参数较少且所需的 FLOPs 少于 DeepSeek 67B,理论上训练 DeepSeek-V2 将比训练 DeepSeek 67B 更经济
- 尽管训练一个 MoE 模型会引入额外的通信开销,但通过相应的操作和通信优化,DeepSeek-V2 的训练可以达到相对较高的模型 FLOPs 利用率 (MFU)
- 在对 H800 集群的实际训练中,每训练一万亿个 token,DeepSeek 67B 需要 300.6K GPU 小时,而 DeepSeek-V2 仅需 172.8K GPU 小时,即稀疏的 DeepSeek-V2 比密集的 DeepSeek 67B 节省了 42.5% 的训练成本
在推理效率上
- 为了高效地部署DeepSeek-V2服务,首先将其参数转换为FP8精度。此外,我们还对DeepSeek-V2进行KV缓存量化(Hooper等,2024;赵等,2023),以进一步将其KV缓存中的每个元素平均压缩到6位
得益于MLA和这些优化,实际部署的DeepSeek-V2所需的KV缓存显著少于DeepSeek 67B,因此可以服务更大的批处理大小 - 基于实际部署的DeepSeek 67B服务的提示和生成长度分布评估了DeepSeek-V2的生成吞吐量
在单个节点上配备8个H800 GPU,DeepSeek-V2实现了超过每秒50K个token的生成吞吐量,是DeepSeek 67B最大生成吞吐量的5.76倍
此外,DeepSeek-V2 的提示输入吞吐量超过每秒 100K 个token
3.2 对齐:监督微调与强化学习
3.2.1 DeepSeek-V2的一些微调、评估细节
基于之前DeepSeek-AI,他们整理了包含 150 万实例的指令微调数据集,其中包括 120 万个有用性实例和 30 万个安全性实例
与初始版本相比,改进了数据质量,以减少幻觉反应并提高写作能力且对 DeepSeek-V2 进行了 2 个周期的微调,学习率设置为 5 × 10−6
为了评估 DeepSeek-V2 Chat(SFT)
- 主要包括基于生成的基准测试,除了几个具有代表性的多项选择任务(MMLU 和 ARC)
- 且还对 DeepSeek-V2 Chat(SFT)进行了指令跟随评估(IFEval),使用提示级松散准确率作为指标
- 此外,我们使用2023年9月1日至2024年4月1日期间的LiveCodeBench (Jain et al., 2024)问题来评估聊天模型
- 除了标准基准测试外,还在开放式对话基准测试中评估了模型,包括MT-Bench (Zheng et al., 2023)、AlpacaEval 2.0 (Dubois et al., 2024)和AlignBench (Liu et al., 2023)
3.2.2 DeepSeek-V2通过GRPO训练策略模型
为了进一步释放DeepSeek-V2的潜力并使其与人类偏好对齐,进行强化学习(RL)以调整其偏好,且为了节省强化学习的训练成本,采用了上文第一部分介绍过的GRPO——详见《一文速览DeepSeekMath及GRPO:通俗理解群体相对策略优化GRPO(含DeepSeek-Coder的简介)》
具体来说,对于每个问题,GRPO 从旧策略
中采样一组输出
——即对同一个问题的不同回答,然后通过最大化以下目标来优化策略模型
目标「Specifically, for each question 𝑞, GRPO samples a group of outputs {𝑜1, 𝑜2, · · · , 𝑜𝐺 }from the old policy 𝜋𝜃𝑜𝑙𝑑 and then optimizes the policy model 𝜋𝜃 by maximizing the following objective」
其中和
是超参数;
是优势,使用一组奖励
对应于每组内的输出计算得出
在具体的训练策略上,采用了两阶段的强化学习训练策略,首先进行推理对齐,然后进行人类偏好对齐
- 在第一个推理对齐阶段,我们训练了一个奖励模型
用于代码和数学推理任务,并通过
的反馈优化策略模型
- 在第二个人类偏好对齐阶段,采用了一个多奖励框架,即
一个有帮助的奖励模型
一个安全奖励模型
一个基于规则的奖励模型获取奖励
从而一个响应的最终奖励 𝑜𝑖是
其中 𝑐1, 𝑐2, 和 𝑐3是相应的系数
更多,可以参见原论文
更多推荐
 已为社区贡献15条内容
已为社区贡献15条内容













所有评论(0)