FloodFill算法（DFS+BFS）【上】

733.图形渲染，200.岛屿数量，695.岛屿的最大面积，130.被围绕的区域

加法器+

1197人浏览 · 2024-09-15 22:36:33

加法器+ · 2024-09-15 22:36:33 发布

文章目录

FloodFill算法
733. 图像渲染
题目解析
算法原理
代码实现

200. 岛屿数量
题目解析
算法原理
代码实现

695. 岛屿的最大面积
题目解析
算法原理
代码实现

130. 被围绕的区域
题目解析
算法原理
代码实现

FloodFill算法

FloodFill算法，中文名叫洪水灌溉

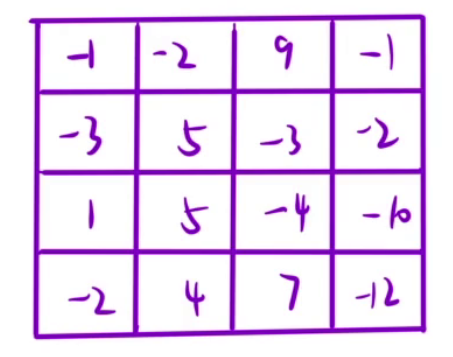
这些模拟一块区域，正数部分表示凸起部分，负数部分表示凹陷部分，在“下雨/发大水”的时候，哪些区域会被覆盖。

这类一般需要解决哪些区域会“填上水”，一共多少块区域或者最大的区域是多少。

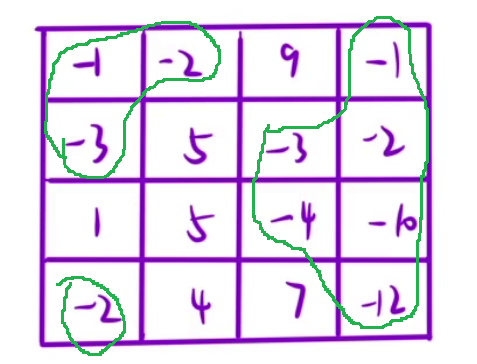
它的本质都是在区域里面性质相同的连通块。

解决这类问题，可以用两种方式：

DFS：深度优先遍历，从某一个点一直走，走到不能再走就返回
BFS：宽度优先遍历，从一个点开始，一层一层走

733. 图像渲染

题目链接：733. 图像渲染

题目解析

题目给我们一个起始位置，把与它相连且像素值相同的改成newColor

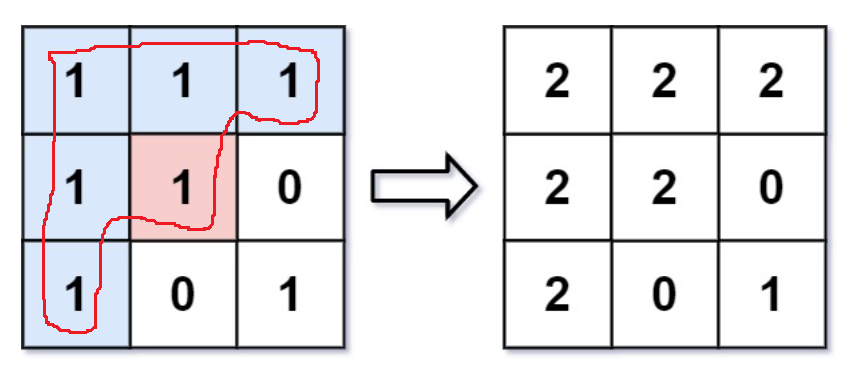
算法原理

DFS：

一条路走到底，走之前先修改数据，走不了然后回溯。

稍微注意一下，然后起始值和目标值一样，可能会走重复的路。

所以需要判断一下，如果相同，直接返回

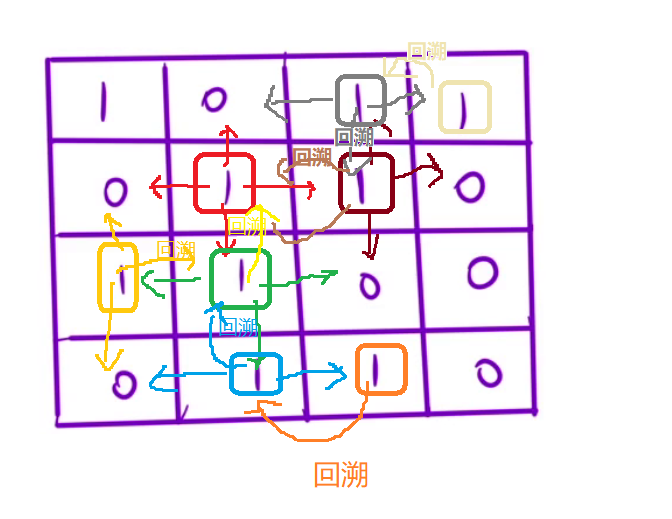
BFS：

从起始位置(1, 1)开始，一层一层向外扩展

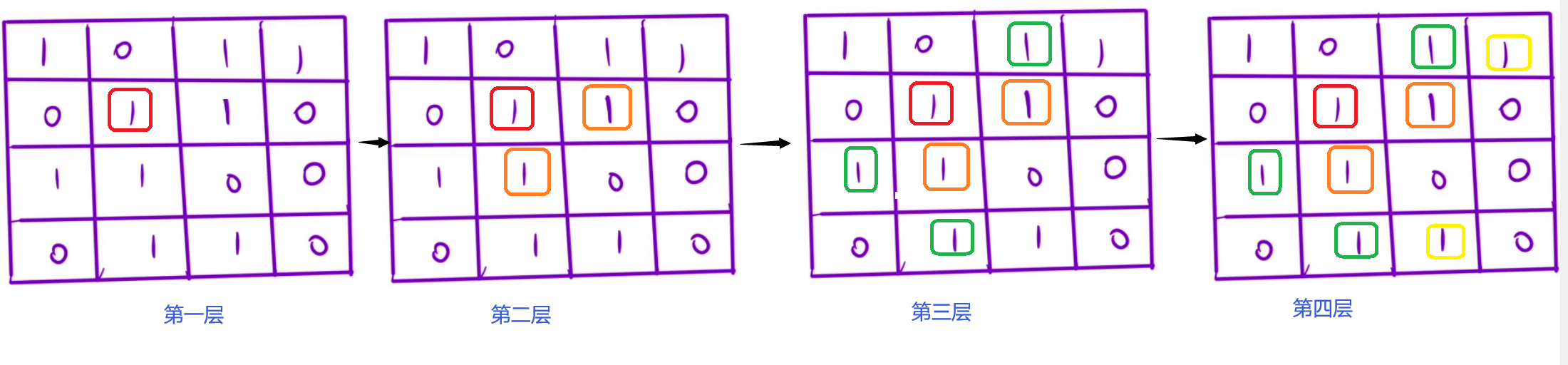
这扩展的时候，就可以修改数据了

代码实现

DFS:

class Solution {
public:
    int m,n;
    int color;
    int target;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int _color)
    {
        color = _color;
        if(image[sr][sc] == color)  return image;
        m = image.size();
        n = image[0].size();
        target = image[sr][sc];
        dfs(image, sr, sc);
        return image;
    }


    void dfs(vector<vector<int>>& image, int pos_x, int pos_y)
    {
        image[pos_x][pos_y] = color;
        for(int k = 0; k < 4; k++)
        {
            int x = dx[k] + pos_x;
            int y = dy[k] + pos_y;
            if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == target)
            {
                //image[x][y] = color;
                dfs(image, x, y);
            }
        }
        //return;
    }
};

BFS:

class Solution {
public:
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
    {
        //起始位置像素值
        int prev = image[sr][sc];  
        if(prev == color)   return image;

        int m = image.size();
        int n = image[0].size();
        queue<pair<int, int>> q;
        q.push({sr, sc});
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            image[a][b] = color;
            for(int i = 0; i < 4; i++)
            {
                int x = dx[i] + a;
                int y= dy[i] + b;
                if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == prev)     
                {
                    q.push({x, y});
                }
            }
        }
        return image;
    }
};

200. 岛屿数量

题目链接：200. 岛屿数量

题目解析

题目的意思就是看有几块连通区域

算法原理

从左往右扫描这个矩阵，当第一次遇到“陆地”的时候，就找到与这块陆地连接的区域

为了避免回溯/扩展回去，两种方法：

将原数组修改
采用一个同等规模的bool vis[][]数组，表示true和false，true扫描过，false未扫描

代码实现

DFS:

class Solution {
public:
    bool vis[301][301];
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    int m, n;
    int ret = 0;
    int numIslands(vector<vector<char>>& grid)
    {
        m = grid.size();
        n = grid[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] == '1' && !vis[i][j])
                {
                    ret++;
                    dfs(grid, i, j);
                }
            }
        }
        return ret;
    }

    void dfs(vector<vector<char>>& grid, int i, int j)
    {
        vis[i][j] = true;
        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >=0 && y < n && grid[x][y] == '1' && !vis[x][y])
            {
                dfs(grid, x, y);
            }
        }
    }
};

BFS:

class Solution {
public:
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    bool vis[301][301];
    int m;
    int n;
    int numIslands(vector<vector<char>>& grid)
    {
        m = grid.size();
        n = grid[0].size();
        int ret = 0;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] == '1' && !vis[i][j])
                {
                    ret++;
                    bfs(grid, i, j);
                }
            }
        }
        return ret;
    }
    void bfs(vector<vector<char>>& grid, int i, int j)
    {
        queue<pair<int, int> > q;
        q.push({i, j});
        vis[i][j] = true;
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = dx[k] + a;
                int y = dy[k] + b;
                if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && !vis[x][y])
                {
                    vis[x][y] = true;
                    q.push({x, y});
                }
            }
        }

    }
};

695. 岛屿的最大面积

题目链接：695. 岛屿的最大面积

题目解析

给我们一个二进制矩阵表示岛屿，其中1表示岛屿、0表示水。

让我们找出面积最大的岛屿（上下左右连通）

算法原理

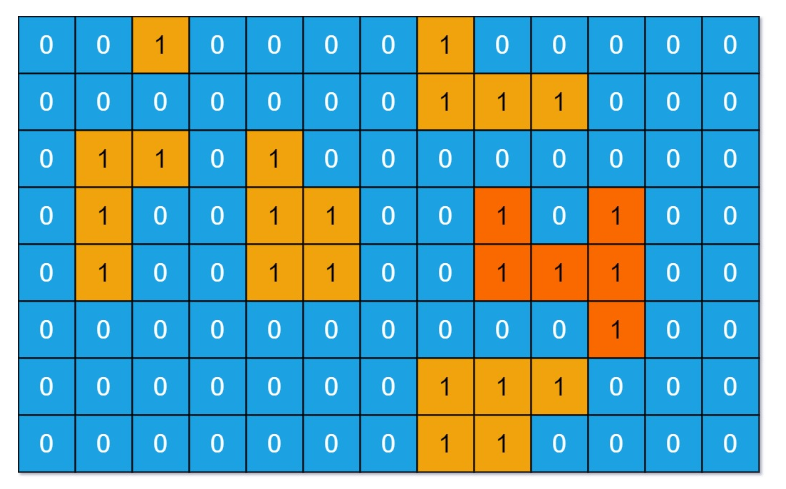
从左往右、从上到下扫描一下矩阵，当遇到没有遍历过的1的时候，然后就进行DFS/BFS：

进入一次dfs，count++，遍历结束之后，就是岛屿面积，只需找出最大值即可
bfs时，加入一次队列，count++，完毕之后，就知道了面积

代码实现

DFS：

class Solution {
public:
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, -1, 1};
    bool vis[51][51];
    int ret, count = 0;
    int m, n;
    int maxAreaOfIsland(vector<vector<int>>& grid)
    {
        m = grid.size();
        n = grid[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] == 1 && !vis[i][j])
                {
                    count = 0;
                    ret = max(ret, dfs(grid, i, j));
                }
            }
        }
        return ret;
    }

    int dfs(vector<vector<int>>& grid, int i, int j)
    {
        vis[i][j] = true;
        count++;
        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1)
            {
                dfs(grid, x, y);
            }
        }
        return count;
    }
};

BFS：

class Solution {
public:
    bool vis[51][51];
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    int m;
    int n;
    int maxAreaOfIsland(vector<vector<int>>& grid)
    {
        m = grid.size();
        n = grid[0].size();
        int ret = 0;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] && !vis[i][j])
                {
                    ret = max(ret, bfs(grid,i, j));
                }
            }
        }
        return ret;
    }

    int bfs(vector<vector<int>>& grid, int i, int j)
    {
        int count = 0;
        queue<pair<int, int>> q;
        q.push({i, j});
        vis[i][j] = true;
        count++;
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y])
                {
                    count++;
                    q.push({x, y});
                    vis[x][y] = true;
                }
            }
        }
        return count;
    }
};

130. 被围绕的区域

题目链接：130. 被围绕的区域

题目解析

给我们一个矩阵，里面只有X和O，找出被X包围的O

必须是上下左右都有X才是被包围

算法原理

这里可以直接遍历，遇见O就修改成X，但是这样如果边界有X，此时又要返回去，重新改回来，这要涉及分情况讨论。

正难则反：

遍历四条边，如果有O，对边上的O做一次dfs/bfs，然后把这些连通块修改成一个无关的字符，然后遍历一次矩阵，此时的O一定是被包围的，直接修改即可

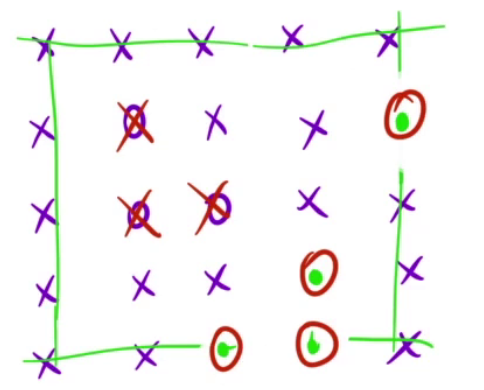
代码实现

DFS：

class Solution {
public:
    int m, n;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    void solve(vector<vector<char>>& board)
    {
        m = board.size();
        n = board[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if((i == 0 || j == 0 || i == m-1 || j == n-1) && board[i][j] == 'O')
                {
                    //cout << 1 << endl;
                    dfs(board, i, j);
                }
            }
        }

        for(auto& e : board)
        {
            for(auto&ch : e)
            {
                if(ch == '.')
                    ch = 'O';
                else
                    ch = 'X';
            }
        }
    }

    void dfs(vector<vector<char>>& board, int i, int j )
    {
        board[i][j] = '.';
        for(int k = 0; k < 4; k++)
        {
            int x = dx[k] + i;
            int y = dy[k] + j;
            if(x >= 0 && y >= 0 && x < m && y < n && board[x][y] == 'O')
            {
                dfs(board, x, y);
            }
        }
    }
};

BFS：

class Solution {
public:
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, -1, 1};
    int m;
    int n;
    char label = '.';
    void solve(vector<vector<char>>& board)
    {
        m = board.size();
        n = board[0].size();
        for(int j = 0; j < n; j++)
        {
            if(board[0][j] == 'O')
            {
                bfs(board, 0, j);
            }
            if(board[m-1][j] == 'O')
            {
                bfs(board, m-1, j);
            }
        }

        for(int i = 0; i < m; i++)
        {
            if(board[i][0] == 'O')
            {
                bfs(board, i, 0);
            }
            if(board[i][n-1] == 'O')
            {
                bfs(board, i, n-1);
            }
        }

        //修改和还原
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(board[i][j] == label)
                {
                    board[i][j] = 'O';
                }
                else
                {
                    board[i][j] = 'X';
                }
            }
        }
    }

    void bfs(vector<vector<char>>& board, int i, int j)
    {
        queue<pair<int, int>> q;
        q.push({i, j});
        board[i][j] = label;
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = dx[k] + a;
                int y = dy[k] + b;
                if(x >= 0 && x < m && y > 0 && y < n && board[x][y] == 'O')
                {
                    board[x][y] = label;
                    q.push({x, y});
                }
            }
        }

    }
};

松山湖开发者村综合服务平台

助力广东及东莞地区开发者，代码托管、在线学习与竞赛、技术交流与分享、资源共享、职业发展，成为松山湖开发者首选的工作与学习平台

更多推荐

深入浅出Python——Python基础语法全解

前言：Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。文章目录一、Python简介1. 了解Python2. Python介绍3. Python特点4. Python发展历史5. Python版本二、Python解释器1. 解释器的作用2. 解释器的安装三、PyCharm安装与使用1. PyCharm的作用2. PyCharm安装与使用四、注释1. 注释的作用2. 注