朴素贝叶斯算法（Naive Bayesian algorithm）是在贝叶斯算法的基础上假设特征变量相互独立的一种分类方法，是贝叶斯算法的简化，常用于文档分类和垃圾邮件过滤。当“特征变量相互独立”的假设条件能够被有效满足时，朴素贝叶斯算法具有算法比较简单、分类效率稳定、所需估计参数少、对缺失数据不敏感等种种优势。而在实务中“特征变量相互独立”的假设条件往往不能得到满足，这在一定程度上降低了贝叶斯分类算法的分类效果，但这并不意味着朴素贝叶斯算法在实务中难以推广，反而它是堪与经典的“决策树算法”比肩的应用最为广泛的分类算法之一。本章我们讲解朴素贝叶斯算法的基本原理，并结合具体实例讲解该算法在Python中的实现与应用。

朴素贝叶斯算法分类及适用条件

与其他机器学习算法相比，朴素贝叶斯算法所需要的样本量比较少（当然样本量肯定是多多益善），样本量少于特征变量数目，那么估计效果也会被削弱。对比支持向量机、随机森林等算法，朴素贝叶斯算法往往估计效果偏弱，但胜在运行速度更快。Python的sklearn模块有四种朴素贝叶斯算法，包括高斯朴素贝叶斯、多项式朴素贝叶斯、补集朴素贝叶斯、二项式朴素贝叶斯。

（1）高斯朴素贝叶斯（Gaussian Naive Bayes）

该算法假设每个特征变量的数据都服从高斯分布（也就是正态分布），用来估计每个特征下每个类别上的条件概率。高斯朴素贝叶斯的决策边界是曲线，可以是环形也可以是弧线。高斯朴素贝叶斯擅长处理连续型特征变量。相对于前面介绍的Logistic回归，如果算法的目的是获得对概率的预测，并且希望越准确越好，那么应该首选Logistic算法；而如果数据十分复杂，或者满足稀疏矩阵的条件（在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律，则称该矩阵为稀疏矩阵），那么高斯朴素贝叶斯算法就更占优势。

（2）多项式朴素贝叶斯（Multinomial Naive Bayes）

该算法通常被用于文本分类，它假设所有特征变量是离散型特征变量，所有特征变量都符合多项式分布。多项式分布来源于统计学中的多项式实验，多项式实验的概念是：在n次重复试验中每项试验都有不同的可能结果，但在任何给定的试验中，特定结果发生的概率是不变的。多项式朴素贝叶斯算法擅长处理分类型特征变量，但受到样本不均衡问题（即分类任务中不同类别的训练样本数目差别很大的情况，一般地，样本类别比例（Imbalance Ratio）（多数类vs少数类）明显大于1:1（如5:1）就可以归为样本不均衡问题）影响较为严重。

（3）补集朴素贝叶斯（Complement Naive Bayes）

该算法是前述多项式朴素贝叶斯算法的改进，不仅能够解决样本不均衡问题，还在一定程度上放松了“所有特征变量之间条件独立的朴素假设”。补集朴素贝叶斯在召回率方面表现较为出色，如果算法的目的是找到少数类（存在异常行为的员工、存在洗钱行为等），则补集朴素贝叶斯算法是一种不错的选择。

4）二项式朴素贝叶斯（Bernoulli Naive Bayes）

也称伯努利朴素贝叶斯，该算法假设所有特征变量是离散型特征变量，所有特征变量都符合伯努利分布（二项分布，取值为两个，注意这两个值并不必然为0、1取值，也可以为1、2取值等）。二项式朴素贝叶斯算法要求将特征变量取值转换为二分类特征向量，如果某特征变量本身不是二分类的，那么可以使用类中专门用来二值化的参数binarize来转换数据，使它符合算法。

以“数据8.1”文件和“数据8.2”文件中的数据为例进行讲解。“数据8.1”记录的是某商业银行在山东地区的部分支行的经营数据（虚拟数据，不涉及商业秘密），变量包括这些商业银行全部支行的V1（转型情况）、V2（存款规模）、V3（EVA）、V4（中间业务收入）、V5（员工人数）。但与“数据7.1”不同的是，V1（转型情况）分为两个类别：“0”表示“未转型网点”；“1”表示“已转型网点。

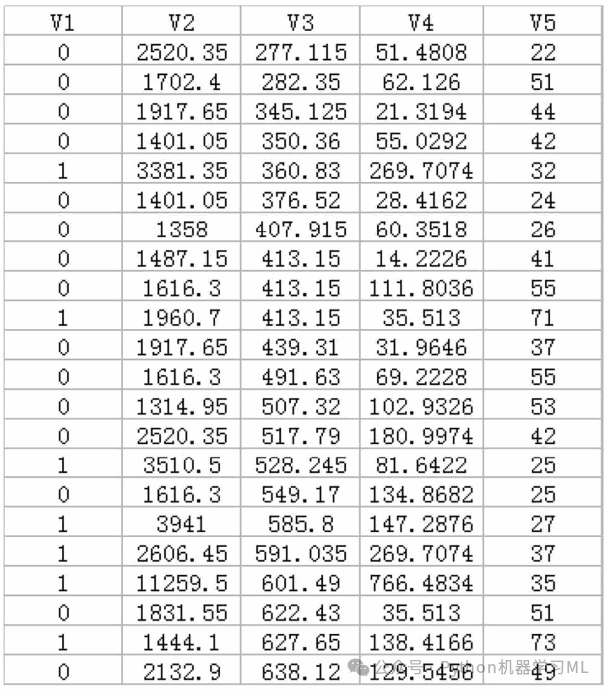
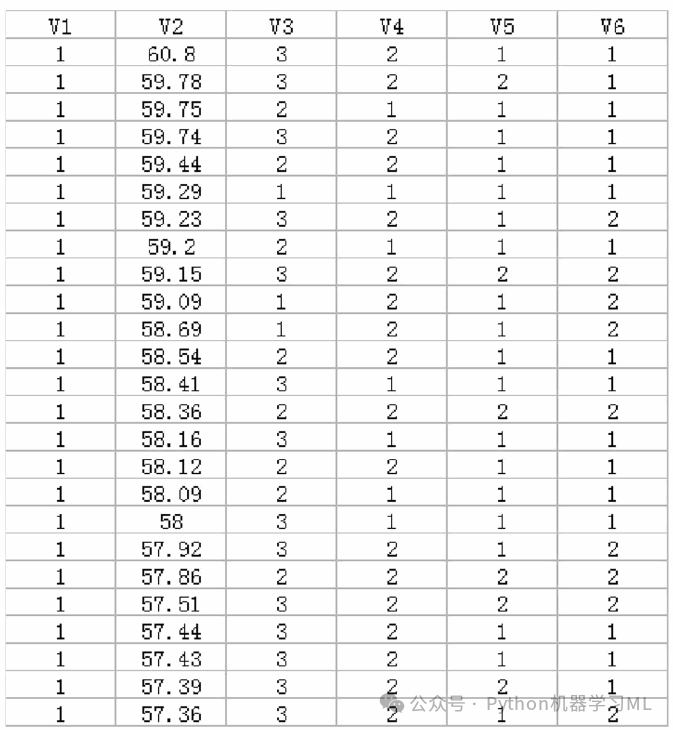
针对“数据8.1”的朴素贝叶斯模型，我们以V1（转型情况）为响应变量，以V2（存款规模）、V3（EVA）、V4（中间业务收入）、V5（员工人数）为特征变量。不难发现，各个特征变量均为连续型变量，所以我们使用高斯朴素贝叶斯算法进行拟合。“数据8.2”的案例数据是来自XX在线小额贷款金融公司（虚拟名，如有雷同纯属巧合）的2417个存量客户的信息数据，具体包括客户的V1（信用情况）、V2（年龄）、V3（贷款收入比）、V4（名下贷款笔数）、V5（教育水平）、V6（是否为他人提供担保）等。由于客户信息数据涉及客户隐私和消费者权益保护，也涉及商业机密，因此本章在介绍时进行了适当的脱密处理，对于其中的部分数据也进行了必要的调整。针对“数据8.2”的朴素贝叶斯模型，我们以V1（信用情况）为响应变量，其中分类为“0”表示“未违约客户”，分类为“1”表示“违约客户”；V2（年龄）、V3（贷款收入比）、V4（名下贷款笔数）、V5（教育水平）、V6（是否为他人提供担保）为特征变量。其中V2（年龄）为连续变量，其他变量为分类变量；V3（贷款收入比）取值为“1”“2”“3”分别表示“40%及以下”“40%～70%”“70%及以上”；V4（名下贷款笔数）取值为“1”“2”分别表示“3笔及以下”“4笔及以上”；V5（教育水平）取值为“1”“2”分别表示“大学专科及以下”“大学本科及以上”；V6（是否为他人提供担保）取值为“1”“2”分别表示“有对外担保”“无对外担保”。“数据8.2”文件中的数据内容如图8.2所示。不难发现，数据集中大部分特征变量为分类变量，其中V3（贷款收入比）有3类取值，而V4（名下贷款笔数）、V5（教育水平）、V6（是否为他人提供担保）这三个变量均为二项分布，所以我们使用多项式朴素贝叶斯算法、补集朴素贝叶斯算法、二项式朴素贝叶斯算法进行拟合。

1、载入分析所需要的模块和函数

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNBfrom sklearn.naive_bayes import MultinomialNBfrom sklearn.naive_bayes import ComplementNBfrom sklearn.naive_bayes import BernoulliNBfrom sklearn.metrics import cohen_kappa_score#from sklearn.metrics import plot_roc_curvefrom sklearn.metrics import confusion_matrixfrom sklearn.metrics import classification_reportfrom sklearn.model_selection import StratifiedKFoldfrom sklearn.model_selection import GridSearchCVfrom mlxtend.plotting import plot_decision_regionsfrom warnings import simplefiltersimplefilter(action='ignore', category=FutureWarning)

2、高斯朴素贝叶斯算法示例

#8.3.1  数据读取及观察data=pd.read_csv('数据8.1.csv')data.info()data.isnull().values.any()data.V1.value_counts()data.V1.value_counts(normalize=True)#8.3.2  将样本示例全集分割为训练样本和测试样本X = data.drop(['V1'],axis=1)#设置特征变量，即除V1之外的全部变量y = data['V1']#设置响应变量，即V1X_train, X_test, y_train, y_test =  train_test_split(X,y,test_size=0.3, stratify=y, random_state=123)

3、高斯朴素贝叶斯算法拟合

model = GaussianNB()model.fit(X_train, y_train)model.score(X_test, y_test)

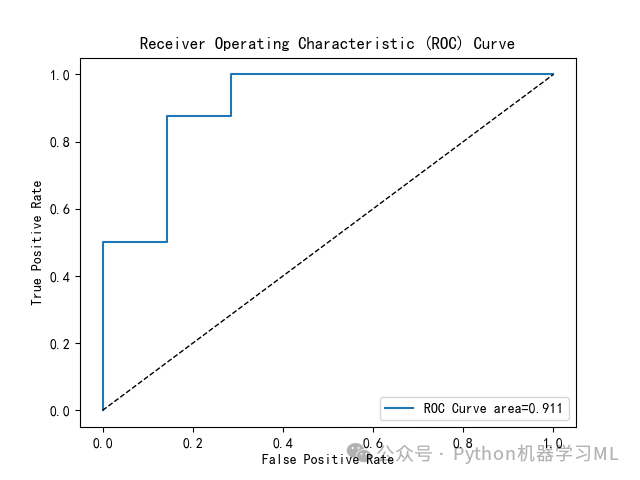
4、绘制ROC曲线

plt.rcParams['font.sans-serif'] = ['SimHei']#解决图表中中文显示问题from sklearn.metrics import roc_curve,roc_auc_score
# 假设 y_true 和 y_score 是你的真实标签和模型预测的概率得分predict_target_prob=model.predict_proba(X_test)fpr, tpr, thresholds = roc_curve(y_test, predict_target_prob[:,1])# 计算AUC值auc = roc_auc_score(y_test, predict_target_prob[:,1])print("AUC值：", auc)# 绘制 ROC 曲线plt.plot(fpr, tpr, label='ROC Curve area=%.3f'%auc)plt.plot(fpr, fpr, 'k--', linewidth=1)plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver Operating Characteristic (ROC) Curve')plt.legend()plt.show()plt.savefig('ROC曲线.png')

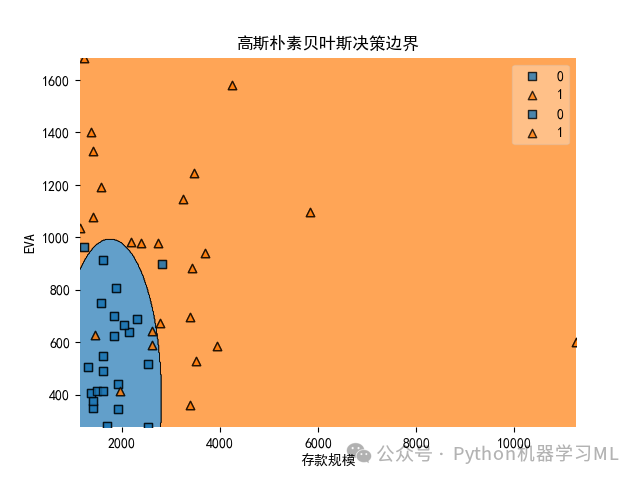
5、运用两个特征变量绘制高斯朴素贝叶斯决策边界图

X2 = X.iloc[:, 0:2]model = GaussianNB()model.fit(X2, y)model.score(X2, y)plt.rcParams['axes.unicode_minus']=False# 解决图表中负号不显示问题。plt.rcParams['font.sans-serif'] = ['SimHei']#解决图表中中文显示问题plot_decision_regions(np.array(X2), np.array(y), model)plt.xlabel('存款规模')#将x轴设置为'存款规模'plt.ylabel('EVA')#将y轴设置为'EVA'plt.title('高斯朴素贝叶斯决策边界')#将标题设置为'高斯朴素贝叶斯决策边界'plt.savefig('高斯朴素贝叶斯决策边界.png')

6、多项式、补集、二项式朴素贝叶斯算法示例

#8.4.1  数据读取及观察data=pd.read_csv('数据8.2.csv')data.V1.value_counts()#观察样本示例全集中响应变量的分类计数值data.V1.value_counts(normalize=True)#观察样本示例全集中响应变量的分类占比#8.4.2  将样本示例全集分割为训练样本和测试样本X = data.drop(['V1'],axis=1)#设置特征变量，即除V1之外的全部变量y = data['V1']#设置响应变量，即V1X_train, X_test, y_train, y_test =  train_test_split(X,y,test_size=0.3, stratify=y, random_state=123)#8.4.3  多项式、补集、二项式朴素贝叶斯算法拟合#1、多项朴素贝叶斯方法model = MultinomialNB(alpha=0)#采取多项朴素贝叶斯方法，不进行拉普拉斯修正model.fit(X_train, y_train)#基于训练样本，使用fit方进行拟合model.score(X_test, y_test)#基于测试样本，计算模型预测准确率
model = MultinomialNB(alpha=1)#采取多项朴素贝叶斯方法，进行拉普拉斯修正model.fit(X_train, y_train)#基于训练样本，使用fit方进行拟合model.score(X_test, y_test)#基于测试样本，计算模型预测准确率#2、补集朴素贝叶斯方法model = ComplementNB(alpha=1)#采取补集朴素贝叶斯方法，进行拉普拉斯修正model.fit(X_train, y_train)#基于训练样本，使用fit方进行拟合model.score(X_test, y_test)#基于测试样本，计算模型预测准确率#3、二项朴素贝叶斯方法model = BernoulliNB(alpha=1)#采取二项朴素贝叶斯方法，进行拉普拉斯修正model.fit(X_train, y_train)#基于训练样本，使用fit方进行拟合model.score(X_test, y_test)#基于测试样本，计算模型预测准确率
model = BernoulliNB(binarize=2, alpha=1)#采取二项朴素贝叶斯方法，设置参数binarize=2，进行拉普拉斯修正model.fit(X_train, y_train)#基于训练样本，使用fit方进行拟合model.score(X_test, y_test)#基于测试样本，计算模型预测准确率

7、寻求二项式朴素贝叶斯算法拟合的最优参数

（1）通过将样本分割为训练样本、验证样本、测试样本的方式寻找最优参数X_trainval, X_test, y_trainval, y_test =  train_test_split(X, y, test_size=0.3, stratify=y, random_state=10)#随机抽取30%的样本作为测试集。

X_train, X_val, y_train, y_val =  train_test_split(X_trainval, y_trainval, test_size=0.2, stratify=y_trainval, random_state=100)#从剩余的70%的样本集（训练集+验证集）中随机抽取20%作为验证集y_train.shape, y_val.shape, y_test.shape#观察样本集形状，得到各样本集的样本容量。best_val_score = 0for binarize in np.arange(0, 5.5, 0.5):    for alpha in np.arange(0, 1.1, 0.1):        model = BernoulliNB(binarize=binarize, alpha=alpha)        model.fit(X_train, y_train)        score = model.score(X_val, y_val)         if score > best_val_score:            best_val_score = score            best_val_parameters = {'binarize': binarize, 'alpha': alpha}print(best_val_score)#计算验证集的最优预测准确率print(best_val_parameters)#得到最优参数model = BernoulliNB(**best_val_parameters)#使用前面得到的最优参数构建伯努利朴素贝叶斯模型model.fit(X_trainval, y_trainval)#使用前述70%的样本集（训练集+验证集）进行伯努利朴素贝叶斯估计model.score(X_test, y_test) #输出基于测试样本得到的预测准确率  

（2）采用10折交叉验证方法寻找最优参数

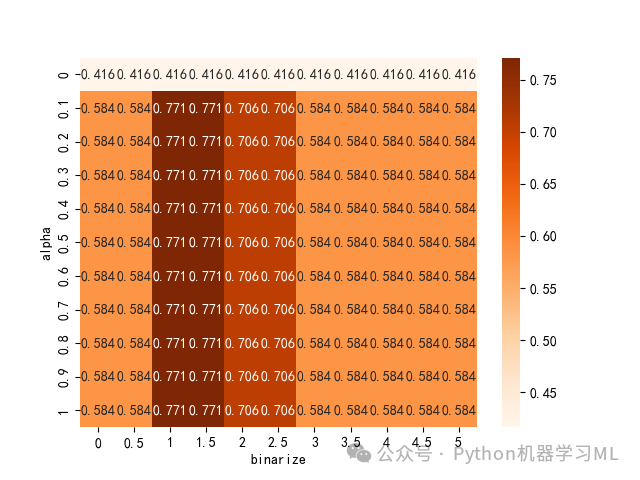
param_grid = {'binarize': np.arange(0, 5.5, 0.5), 'alpha': np.arange(0, 1.1, 0.1)}#定义字典形式的参数网络kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)#保持每折子样本中响应变量各类别数据占比相同model = GridSearchCV(BernoulliNB(), param_grid, cv=kfold)#构建伯努利朴素贝叶斯模型，使用上步得到的参数网络，使用10折交叉验证方法进行交叉验证model.fit(X_trainval, y_trainval)#使用前述70%的样本集（训练集+验证集）进行伯努利朴素贝叶斯估计model.score(X_test, y_test)#输出基于测试样本得到的预测准确率model.best_params_#输出最优参数model.best_score_ #计算最优预测准确率outputs = pd.DataFrame(model.cv_results_)#得到每个参数组合的详细交叉验证信息，并转化为数据框形式pd.set_option('display.max_columns', None)outputs.head(3)#展示前3行scores = np.array(outputs.mean_test_score).reshape(11,11)#将平均预测准确率组成11*11矩阵ax = sns.heatmap(scores, cmap='Oranges', annot=True, fmt='.3f')# 绘制热图将10折交叉验证方法寻找最优参数过程可视化ax.set_xlabel('binarize')ax.set_xticklabels([0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5,5])ax.set_ylabel('alpha')ax.set_yticklabels([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1])#plt.tight_layout()plt.show()plt.savefig('热图.png')

8、最优二项式朴素贝叶斯算法模型性能评价

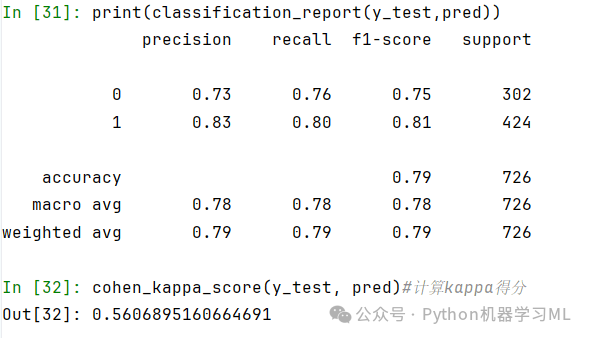
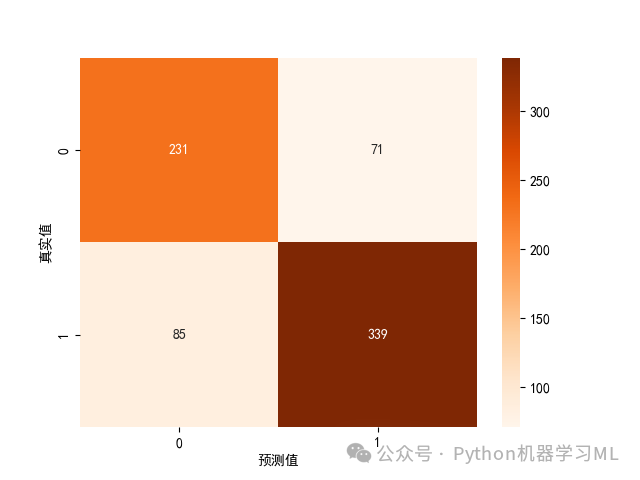
prob = model.predict_proba(X_test)prob[:5]pred = model.predict(X_test)pred[:5]print(confusion_matrix(y_test, pred))#混淆矩阵热力图ax = sns.heatmap(confusion_matrix(y_test, pred), cmap='Oranges', annot=True, fmt='d')ax.set_xlabel('预测值')ax.set_ylabel('真实值')plt.show()
print(classification_report(y_test,pred))cohen_kappa_score(y_test, pred)#计算kappa得分

需要数据集请关注公众号：Python机器学习ML  回复  数据