目的

1. 掌握常用可视化软件与工具：学习和熟练使用常用的数据可视化软件和工具，如Matplotlib、Seaborn、Plotly、Tableau等。这些工具提供了用于创建图表、图形和可视化效果的函数和方法，使数据更容易理解和解释。
2. 能够通过可视化软件或工具进行相关数据可视化操作：掌握如何使用所选的可视化工具来操作和呈现数据。这包括绘制不同类型的图表（例如线图、柱状图、饼图、散点图、热图等）以及进行数据的处理、整理和转换以获得所需的可视化结果。
3. 了解可视化软件与工具的应用：理解数据可视化工具的应用领域和重要性。数据可视化是数据分析和数据传达的关键组成部分，它可以用于展示趋势、关系、模式和异常，以便做出决策、发现见解或传达信息。在各种领域中，包括业务分析、科学研究、市场营销、医疗保健等，数据可视化都具有广泛的应用。

内容

1. 气泡图和散点图的对比

   • 气泡图：气泡图是在散点图的基础上增加了一个维度的数据。每个数据点不仅有横纵坐标，还有一个表示大小的圆。圆的大小可以用来表示多出的那一维数据的大小。
   • 散点图：散点图仅使用两个维度的数据，即横纵坐标，用于展示数据点之间的关系。

2. 茎叶图

   • 思路：将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面。这样可以清楚地看到每个主干后面的几个数，每个数具体是多少。
   • 用途：茎叶图常用于展示数据的分布情况，特别是在小样本数据集中非常有用。

3. 层次结构数据可视化

   • 树型结构：层次结构可以被抽象成树型（Tree）结构，它是以分支关系定义的非线性结构。
   • 节点-链接法：将单个个体绘制成一个节点，节点之间的连线表示个体之间的层次关系。这种方法直观地展示了层次结构，适用于较小的数据集。
   • 空间填充法：用空间中的分块区域表示数据中的个体，并用外层区域对内层区域的包围表示彼此之间的层次关系。这种方法适用于较大的数据集，可以避免节点-链接法中的交叉和混乱。

树图绘制

目的

1. 掌握树图的布局方式：了解树图的两种布局方式——正交布局和径向布局，并学会如何设置布局方向。
2. 熟悉树图的标记图形：了解ECharts提供的标记类型，并学会如何在树图中使用这些标记类型。
3. 绘制树图：使用PyEcharts库绘制树图，并设置不同的布局方式和标记图形。

步骤

1. 数据准备

   • 准备一个树形结构的数据集，包含多个层级的节点。

2. 绘制树图

   • 使用PyEcharts库绘制树图，并设置不同的布局方式和标记图形。

参考代码

from pyecharts import options as opts
from pyecharts.charts import Tree

# 树形结构数据
data = [
    {
        "children": [
            {"name": "B"},
            {
                "children": [{"children": [{"name": "I"}], "name": "E"}, {"name": "F"}],
                "name": "C",
            },
            {
                "children": [
                    {"children": [{"name": "J"}, {"name": "K"}], "name": "G"},
                    {"name": "H"},
                ],
                "name": "D",
            },
        ],
        "name": "A",
    }
]

# 创建树图
c = (
    Tree()
    .add(
        "",
        data,
        orient="TB",  # 设置布局方向为从上到下
        layout="radial",  # 设置布局方式为径向布局
        symbol="roundRect",  # 设置标记图形为圆角矩形
        symbol_size=[15, 20],  # 设置标记图形的大小
    )
    .set_global_opts(title_opts=opts.TitleOpts(title="Tree-基本示例"))
)

# 渲染树图
c.render_notebook()

结果与分析

1. 树图的布局

   • 正交布局：当 layout = 'orthogonal' 时，可以通过 orient 参数设置布局方向。例如，orient="TB" 表示从上到下，orient="LR" 表示从左到右。
   • 径向布局：当 layout = 'radial' 时，树图将以根节点为中心，向外扩展。这种布局方式适合展示层级较深的树形结构。

2. 标记的图形

   • 通过 symbol 参数可以设置节点的标记图形。例如，symbol="roundRect" 设置节点为圆角矩形。
   • 通过 symbol_size 参数可以设置标记图形的大小。例如，symbol_size=[15, 20] 设置标记图形的宽度为15，高度为20。

力引导布局算法

目的

1. 了解力引导布局算法：掌握力引导布局算法的基本原理，了解其只能达到局部优化而不能达到全局优化的特点。
2. 熟悉力引导布局的改进算法：了解力引导布局的改进算法主要针对效率的优化，优化思路大致分为减少迭代次数和降低每次迭代的时间复杂度。
3. 实现力引导布局：使用 networkx 和 matplotlib 库实现力引导布局算法，并绘制图的可视化结果。

参考代码

import networkx as nx
import matplotlib.pyplot as plt

# 创建一个简单的图
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 5), (5, 1), (1, 3), (2, 4)])

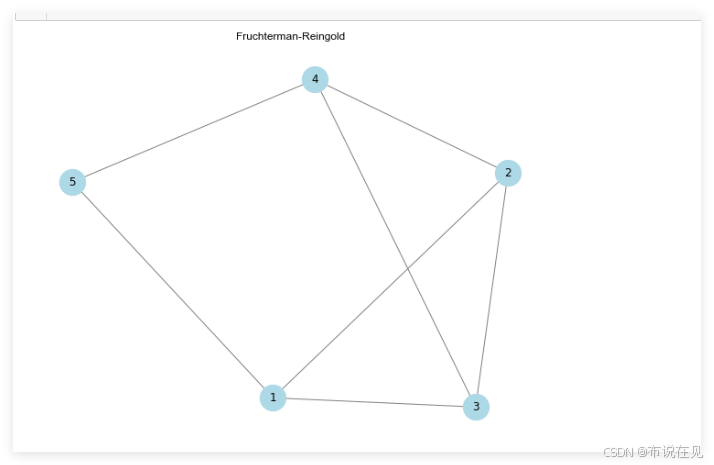
# 使用力引导布局算法
pos = nx.spring_layout(G)

# 绘制图
plt.figure(figsize=(8, 6))
nx.draw(G, pos=pos, with_labels=True, node_size=800, node_color='lightblue', edge_color='gray', node_shape='o')
plt.title("Fruchterman-Reingold Layout")
plt.show()

结果与分析

1. 力引导布局算法的基本原理

   • 力引导布局算法通过模拟物理系统中的力作用，使节点分布更加自然。每个节点受到吸引力和排斥力的作用，最终达到一个相对稳定的布局。
   • 由于力引导布局算法是一个迭代过程，初始位置对最后优化结果的影响较大。不同的初始位置可能会导致不同的最终布局。

2. 力引导布局的改进算法

   • 减少迭代次数：通过预处理或启发式方法减少需要迭代的次数，例如使用多尺度方法或基于密度的方法。
   • 降低每次迭代的时间复杂度：通过优化力的计算方法，减少每次迭代的时间复杂度，例如使用 Barnes-Hut 近似方法。

3. 实验结果

   • 使用 spring_layout 函数生成的力引导布局图显示了节点的自然分布。节点之间的距离适中，避免了节点重叠，使得图的结构清晰可见。

总结

新的一天开始了，希望我们今天充满活力和灵感！无论是继续进行数据可视化的实验，还是有其他的工作和学习计划，愿这一天都能带给我们新的收获和进步。