无人船 | 图解推导三自由度USV的运动学和动力学建模
本文从六自由度无人船的定义出发,详细推到了USV的运动学和动力学模型,为USV规划、控制算法设计打下基础
1 参考坐标系定义
USV的数学模型分为运动学和动力学两个部分,其中运动学描述了USV作为质点的几何运动规律;动力学描述了USV在来自螺旋桨、水扰、风扰等力作用下产生的运动规律。为了更好地表达USV的运动学和动力学模型,定义
-
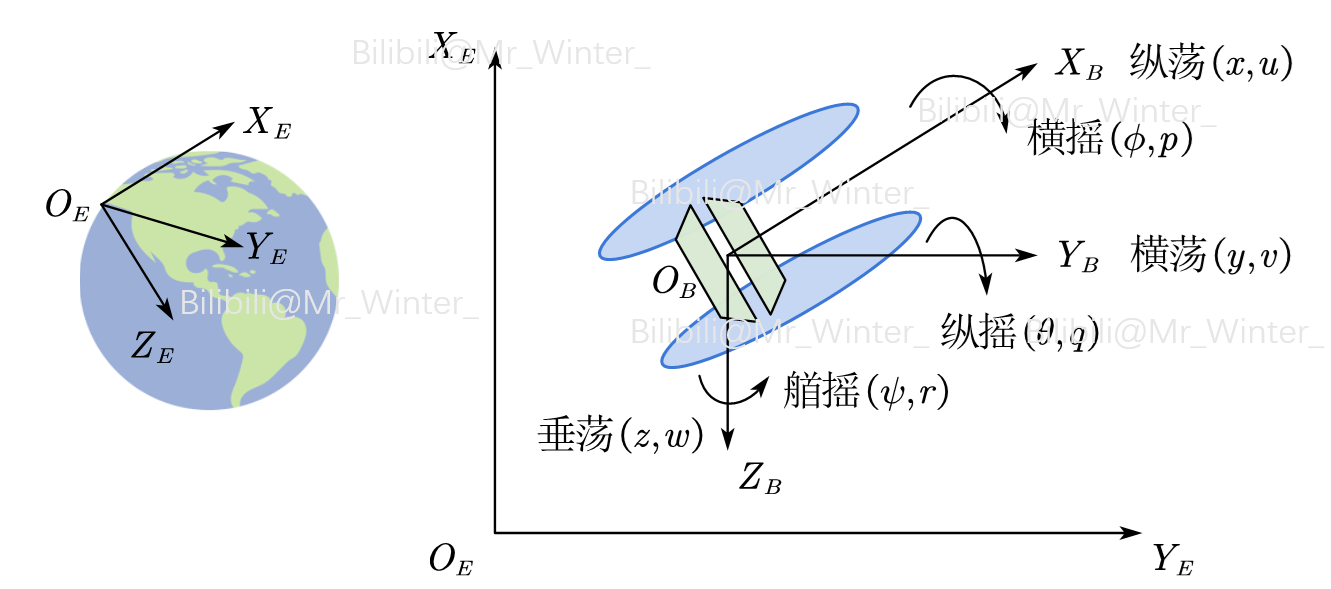
全局坐标系 O E − X E Y E Z E O_E-X_EY_EZ_E OE−XEYEZE:用于描述USV的位置和姿态。全局坐标系以地球表面某一点为原点, O E X E O_EX_E OEXE指向地理正北方向, O E Y E O_EY_E OEYE指向地理正东方向, O E Z E O_EZ_E OEZE指向地心,其中 O E Z E O_EZ_E OEZE是 O E X E O_EX_E OEXE轴和 O E Y E O_EY_E OEYE轴构成平面的法线,且平面 O E X E Y E O_EX_EY_E OEXEYE与地球表面相切
-
船体坐标系 O B − X B Y B Z B O_B-X_BY_BZ_B OB−XBYBZB:用于描述USV受力后位置及姿态的瞬时变化,即线速度或角速度。船体坐标系一般以USV船体重心为原点, O B X B O_BX_B OBXB平行于海平面并指向船艏方向, O B Y B O_BY_B OBYB平行于海平面并指向船右舷方向, O B Z B O_BZ_B OBZB轴指向地心并与水平面垂直
两个坐标系间的关系如图所示

在水面环境下,USV受到多种方向上的外力,需要用多个自由度去描述其复杂的运动状态。根据造船与轮机工程师学会(SNAME)的有关标准,使用如表所示的定义描述船舶在纵荡、横荡、垂荡、横摇、纵摇、艏摇六个自由度上的运动状态。具体而言,坐标 ( x , y , z , ϕ , θ , ψ ) \left( x,y,z,\phi ,\theta ,\psi \right) (x,y,z,ϕ,θ,ψ)表示船舶在全局坐标系下的位置和姿态;其一阶导数坐标 ( u , v , w , p , q , r ) \left( u,v,w,p,q,r \right) (u,v,w,p,q,r)表示船舶在船体坐标系下的平移线速度和转动角速度

2 运动学建模
根据上表定义的USV完整六自由度运动学模型为
{ [ x ˙ y ˙ z ˙ ] = [ cos θ cos ψ sin φ sin θ cos ψ − cos φ sin ψ cos φ sin θ cos ψ + sin φ sin ψ cos θ sin ψ sin φ sin θ sin ψ + cos φ cos ψ cos φ sin θ sin ψ − sin φ cos ψ − sin θ sin φ cos θ cos φ cos θ ] [ u v w ] [ φ ˙ θ ˙ ψ ˙ ] = [ 1 sin φ tan θ cos φ tan θ 0 cos φ − sin φ 0 sin φ / cos θ cos φ / cos θ ] [ p q r ] \begin{cases} \left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{z}\\\end{array} \right] =\left[ \begin{matrix} \cos \theta \cos \psi& \sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi& \cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi\\ \cos \theta \sin \psi& \sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi& \cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi\\ -\sin \theta& \sin \varphi \cos \theta& \cos \varphi \cos \theta\\\end{matrix} \right] \left[ \begin{array}{c} u\\ v\\ w\\\end{array} \right]\\ \left[ \begin{array}{c} \dot{\varphi}\\ \dot{\theta}\\ \dot{\psi}\\\end{array} \right] =\left[ \begin{matrix} 1& \sin \varphi \tan \theta& \cos \varphi \tan \theta\\ 0& \cos \varphi& -\sin \varphi\\ 0& {{\sin \varphi}/{\cos \theta}}& {{\cos \varphi}/{\cos \theta}}\\\end{matrix} \right] \left[ \begin{array}{c} p\\ q\\ r\\\end{array} \right]\\\end{cases} ⎩ ⎨ ⎧ x˙y˙z˙ = cosθcosψcosθsinψ−sinθsinφsinθcosψ−cosφsinψsinφsinθsinψ+cosφcosψsinφcosθcosφsinθcosψ+sinφsinψcosφsinθsinψ−sinφcosψcosφcosθ uvw φ˙θ˙ψ˙ = 100sinφtanθcosφsinφ/cosθcosφtanθ−sinφcosφ/cosθ pqr
USV在水中虽然存在六个自由度上的运动,但是上述完整的运动学模型过于复杂,对运动分析和控制器设计造成困难。考虑到实际应用中USV在垂荡、纵摇及横摇三个自由度上的运动幅度相对很小,一般忽略这三个自由度上的运动状态,即令
w = p = q = z = φ = θ = 0 w=p=q=z=\varphi =\theta =0 w=p=q=z=φ=θ=0
得到简化的三自由度USV运动学模型
[ x ˙ y ˙ ψ ˙ ] = [ cos ψ − sin ψ 0 sin ψ cos ψ 0 0 0 1 ] [ u v r ] ⇒ η = R v \left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\psi}\\\end{array} \right] =\left[ \begin{matrix} \cos \psi& -\sin \psi& 0\\ \sin \psi& \cos \psi& 0\\ 0& 0& 1\\\end{matrix} \right] \left[ \begin{array}{c} u\\ v\\ r\\\end{array} \right] \Rightarrow \boldsymbol{\eta }=\boldsymbol{Rv} x˙y˙ψ˙ = cosψsinψ0−sinψcosψ0001 uvr ⇒η=Rv
3 动力学建模
Fossen建立了统一的船舶动力学模型,将USV的受力分解为刚体力、流体动力、推进力和干扰力
M v ˙ + C ( v ) v + D ( v ) v + g ( η ) = τ + τ E \boldsymbol{M\dot{v}}+\boldsymbol{C}\left( \boldsymbol{v} \right) \boldsymbol{v}+\boldsymbol{D}\left( \boldsymbol{v} \right) \boldsymbol{v}+\boldsymbol{g}\left( \boldsymbol{\eta } \right) =\boldsymbol{\tau }+\boldsymbol{\tau }_E Mv˙+C(v)v+D(v)v+g(η)=τ+τE
上式中 M \boldsymbol{M} M为船体系统的惯性矩阵,由刚体惯性矩阵 M R B \boldsymbol{M}_{RB} MRB和附加质量矩阵 M A \boldsymbol{M}_A MA组成
M = M R B + M A = [ m 11 m 22 m 23 m 32 m 33 ] \boldsymbol{M}=\boldsymbol{M}_{RB}+\boldsymbol{M}_A=\left[ \begin{matrix} m_{11}& & \\ & m_{22}& m_{23}\\ & m_{32}& m_{33}\\\end{matrix} \right] M=MRB+MA= m11m22m32m23m33
其中船舶质量为 m m m, ( x g , y g , z g ) \left( x_g,y_g,z_g \right) (xg,yg,zg)是船舶重心在船体坐标系下的坐标, I z I_z Iz是绕 O B Z B O_BZ_B OBZB转动惯量
M R B = [ m − m y g m m x g − m y g m x g I z ] , M A = − [ X u ˙ X r ˙ Y v ˙ Y r ˙ N u ˙ N v ˙ N r ˙ ] \boldsymbol{M}_{RB}=\left[ \begin{matrix} m& & -my_g\\ & m& mx_g\\ -my_g& mx_g& I_z\\\end{matrix} \right] , \boldsymbol{M}_A=-\left[ \begin{matrix} X_{\dot{u}}& & X_{\dot{r}}\\ & Y_{\dot{v}}& Y_{\dot{r}}\\ N_{\dot{u}}& N_{\dot{v}}& N_{\dot{r}}\\\end{matrix} \right] MRB= m−mygmmxg−mygmxgIz ,MA=− Xu˙Nu˙Yv˙Nv˙Xr˙Yr˙Nr˙
C ( v ) \boldsymbol{C}\left( \boldsymbol{v} \right) C(v)为科氏力-向心力矩阵,由刚体科氏力-向心力矩阵 C R B ( v ) \boldsymbol{C}_{RB}\left( \boldsymbol{v} \right) CRB(v)和附加科氏力-向心力矩阵 C A ( v ) \boldsymbol{C}_A\left( \boldsymbol{v} \right) CA(v)组成
C ( v ) = C R B ( v ) + C A ( v ) = [ 0 0 c 13 0 0 c 23 c 31 c 32 0 ] \boldsymbol{C}\left( \boldsymbol{v} \right) =\boldsymbol{C}_{RB}\left( \boldsymbol{v} \right) +\boldsymbol{C}_A\left( \boldsymbol{v} \right) =\left[ \begin{matrix} 0& 0& c_{13}\\ 0& 0& c_{23}\\ c_{31}& c_{32}& 0\\\end{matrix} \right] C(v)=CRB(v)+CA(v)= 00c3100c32c13c230
其中
C R B ( v ) = [ 0 0 − m ( x g r + v ) 0 0 − m ( y g r − u ) m ( x g r + v ) m ( y g r − u ) 0 ] C A ( v ) = [ 0 0 Y v ˙ v + Y r ˙ r 0 0 − X u ˙ u − Y v ˙ v − Y r ˙ r X u ˙ u 0 ] \boldsymbol{C}_{RB}\left( \boldsymbol{v} \right) =\left[ \begin{matrix} 0& 0& -m\left( x_gr+v \right)\\ 0& 0& -m\left( y_gr-u \right)\\ m\left( x_gr+v \right)& m\left( y_gr-u \right)& 0\\\end{matrix} \right] \\\boldsymbol{C}_A\left( \boldsymbol{v} \right) =\left[ \begin{matrix} 0& 0& Y_{\dot{v}}v+Y_{\dot{r}}r\\ 0& 0& -X_{\dot{u}}u\\ -Y_{\dot{v}}v-Y_{\dot{r}}r& X_{\dot{u}}u& 0\\\end{matrix} \right] CRB(v)= 00m(xgr+v)00m(ygr−u)−m(xgr+v)−m(ygr−u)0 CA(v)= 00−Yv˙v−Yr˙r00Xu˙uYv˙v+Yr˙r−Xu˙u0
D ( v ) \boldsymbol{D}\left( \boldsymbol{v} \right) D(v)为阻尼矩阵,由线性阻尼矩阵 D \boldsymbol{D} D和非线性阻尼矩阵 D n ( v ) \boldsymbol{D}_n\left( \boldsymbol{v} \right) Dn(v)组成
D ( v ) = D + D n ( v ) = [ d 11 d 22 d 23 d 32 d 33 ] \boldsymbol{D}\left( \boldsymbol{v} \right) =\boldsymbol{D}+\boldsymbol{D}_n\left( \boldsymbol{v} \right) =\left[ \begin{matrix} d_{11}& & \\ & d_{22}& d_{23}\\ & d_{32}& d_{33}\\\end{matrix} \right] D(v)=D+Dn(v)= d11d22d32d23d33
其中
D = − [ X u Y v Y r N v N r ] , D n ( v ) = − [ X ∣ u ∣ u ∣ u ∣ Y ∣ v ∣ v ∣ v ∣ + Y ∣ r ∣ v ∣ r ∣ Y ∣ v ∣ r ∣ v ∣ + Y ∣ r ∣ r ∣ r ∣ N ∣ v ∣ v ∣ v ∣ + N ∣ r ∣ v ∣ r ∣ N ∣ v ∣ r ∣ v ∣ + N ∣ r ∣ r ∣ r ∣ ] \boldsymbol{D}=-\left[ \begin{matrix} X_u& & \\ & Y_v& Y_r\\ & N_v& N_r\\\end{matrix} \right] , \boldsymbol{D}_n\left( \boldsymbol{v} \right) =-\left[ \begin{matrix} X_{\left| u \right|u}\left| u \right|& & \\ & Y_{\left| v \right|v}\left| v \right|+Y_{\left| r \right|v}\left| r \right|& Y_{\left| v \right|r}\left| v \right|+Y_{\left| r \right|r}\left| r \right|\\ & N_{\left| v \right|v}\left| v \right|+N_{\left| r \right|v}\left| r \right|& N_{\left| v \right|r}\left| v \right|+N_{\left| r \right|r}\left| r \right|\\\end{matrix} \right] D=− XuYvNvYrNr ,Dn(v)=− X∣u∣u∣u∣Y∣v∣v∣v∣+Y∣r∣v∣r∣N∣v∣v∣v∣+N∣r∣v∣r∣Y∣v∣r∣v∣+Y∣r∣r∣r∣N∣v∣r∣v∣+N∣r∣r∣r∣
g ( η ) \boldsymbol{g}\left( \boldsymbol{\eta } \right) g(η)是由重力和浮力产生的恢复力和力矩。控制力 τ = [ τ u τ v τ r ] T \boldsymbol{\tau }=\left[ \begin{matrix} \tau _u& \tau _v& \tau _r\\\end{matrix} \right] ^T τ=[τuτvτr]T,其中 τ u \tau _u τu、 τ v \tau _v τv、 τ r \tau _r τr分别表示由螺旋桨产生的前进力、横漂力和艏摇力矩
上面涉及到的水动力系数的含义如下所示

至此,USV的运动学和动力学建模完成,本专栏的后续章节都将以本节推导的模型展开规划、控制算法设计
🔥 更多精彩专栏:
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容









所有评论(0)