参考

时间序列预测模型比较分析：SARIMAX、RNN、LSTM、Prophet 及 Transformer

https://mp.weixin.qq.com/s/b4IE-y85zHoW1Ujuy9hDGg

“欣旺达”股价的时序预测（Tushare + Prophet）

时序数据与非时序数据的主要区别在于数据的结构和依赖关系。理解这两者的差异对于选择合适的数据处理方法和模型至关重要。

CICC科普栏目｜时间序列预测的常用方法优缺点对比分析

时序数据 vs 非时序数据的差异与算法选择

时序数据 vs 非时序数据

1. 数据结构

   • 时序数据：具有时间顺序，每个数据点都有一个明确的时间戳，且通常相邻的数据点之间存在相关性（即自相关性）。例如，股票价格、气象数据等。
   • 非时序数据：没有固有的时间顺序，数据点之间的关系不是基于时间的。例如，客户信息、图像分类中的像素值等。

2. 依赖关系

   • 时序数据：数据点之间可能存在时间上的依赖关系，这意味着当前时刻的状态可能受到过去状态的影响。这种特性要求模型能够捕捉到这些依赖关系。
   • 非时序数据：数据点之间通常是独立同分布（i.i.d），也就是说，每个样本都是独立于其他样本，并且来自相同的概率分布。

3. 特征工程

   • 时序数据：经常需要进行特定的特征提取或转换，如滑动窗口、滞后特征（lag features）、差分（differencing）以消除趋势和季节性成分等。
   • 非时序数据：特征工程更多关注于如何从原始数据中提取有意义的信息，比如PCA降维、特征选择等。

4. 预测目标

   • 时序数据：通常用于预测未来的值，这涉及到理解数据中的趋势、周期性和随机波动。
   • 非时序数据：主要用于分类或回归任务，不涉及未来预测的问题。

常见的时序算法

参考：CICC科普栏目｜时间序列预测的常用方法优缺点对比分析

时间序列预测是指利用获得的数据按时间顺序排成序列，分析其变化方向和程度，从而对未来若干时期可能达到的水平进行推测。时间序列预测的基本思想，就是将时间序列作为一个随机变量的一个样本，用概率统计的方法，从而尽可能减少偶然因素的影响。
当比较时间序列预测的常用方法时，可以考虑它们的优点和缺点，以便选择最适合的方法。

移动平均法（MA）：

优点：简单易懂，易于实现；能够平滑数据并捕捉数据的长期趋势；能够处理季节性变动。
缺点：只利用了过去的有限观测，忽略其他影响因素；对离群值敏感；未考虑数据非线性关系。

加权移动平均法（WMA）：

优点：能够更灵活地对过去值赋予不同的权重，以适应不同的数据情况；能够处理季节性变动。
缺点：对权重的选择敏感；对离群值敏感；未考虑数据的非线性关系。

指数平滑法（ES）：

优点：简单易懂易于实现；能够平滑数据并捕捉数据长期趋势；能够自动适应数据的时间变化。
缺点：只利用了过去的有限观测，忽略了其他影响因素；对初始值的选择敏感；未考虑数据的非线性关系。

季节性模型方法：

优点：能够处理季节性变动，捕捉周期性的影响；可以提供季节性调整后的预测结果。
缺点：需要对季节性的周期和幅度有一定的先验知识；对于非周期性的数据预测效果较差。

自回归滑动平均模型（ARMA）：

优点：能够自动捕捉时间序列数据的趋势和周期性；可以处理非平稳数据。
缺点：对模型参数的选择需借助自相关图（ACF）和偏自相关图（PACF），有一定主观性；对离群值敏感。

自回归积分滑动平均模型（ARIMA）：

优点：能够处理非平稳数据，对趋势和周期性进行建模；相对于ARMA模型，可以更好地处理非平稳数据。
缺点：对模型参数的选择需要通过查看自相关图和偏自相关图；对于长期的趋势和季节性变动不适用。

随机森林（Random Forest）：

优点：能够处理多个变量之间的非线性关系；对于大规模数据和高维数据具有较好的扩展性；能够提供特征重要性排序。
缺点：对于时间序列数据，可能需要进行一些预处理，如滑动窗口方法；参数选择较为复杂；模型解释性较差。

神经网络（Neural Network）：

优点：能够处理非线性关系和复杂的时间序列数据；适用于大规模数据的建模和预测；具有一定的自适应性。
缺点：模型参数调整较为困难；数据量和计算资源的要求较高；对于小样本数据可能会过拟合。

长短期记忆网络（LSTM）：

优点：适用于处理长期依赖关系和非线性关系；能够捕捉序列数据中的长期模式和短期波动；对于大规模数据和高维数据有较好的扩展性。
缺点：对于小样本数据可能会过拟合；模型参数的选择和调整较为复杂；对计算资源需求较高。

卷积神经网络（CNN）：

优点：适用于处理具有空间结构的时间序列数据，如图像、声音等；能够捕捉序列数据中的局部模式和特征；对于大规模数据和高维数据有较好的扩展性。
缺点：对于非平稳数据和长期依赖关系的建模相对不足；对于数据的前后关系可能不够充分。

支持向量回归（SVR）：

优点：能够处理非线性关系；对于小样本数据有较好的表现；通过核函数的选择可以适应不同的数据情况。
缺点：对于大规模数据和高维数据的处理较为困难；需要调整超参数，如选择合适的核函数和正则化参数；对离群值敏感。

强化学习：

优点：能够通过与环境的交互来优化预测策略，适用于动态环境的时间序列预测；对于复杂问题和非线性关系有潜力提供较好的解决方案。
缺点：需要大量的训练样本和计算资源；对于任务设定和奖励设计有一定的挑战；对模型的解释性较差。

集成方法：

优点：能够通过组合多个预测模型的结果来提高准确性和稳定性；能够综合不同模型的优势。
缺点：对于模型的选择和集成方式需要一定的经验和判断；对计算资源和训练时间的要求较高。

贝叶斯方法：

优点：能够估计预测的不确定性，提供可信度的区间估计；能够自动更新模型参数和先验概率。
缺点：计算复杂度较高，对于大规模数据可能不适用；对先验知识的依赖性较强；无法处理非线性关系和复杂模型。

随机游走模型：

优点：简单易懂，简单地假设未来值与当前值相等，适用于短期预测。
缺点：没有利用过去的信息，只能作为基准模型；对于长期预测效果较差；无法捕捉趋势和季节性的影响。

非线性时间序列模型：

优点：
能够处理复杂的非线性关系，适用于特定的非线性时间序列数据；有较好的灵活性和泛化能力。
缺点：建模复杂度较高，参数估计和模型解释较为困难；对数据量和计算资源的要求较高；需要充分的领域知识和经验去选择和调整模型。

因子分析：

优点：能够将复杂的时间序列数据分解为主要的共同模式和影响因子；提供有关数据生成过程的进一步理解。
缺点：对数据的先验假设和可解释性要求较高；需要充分的领域知识和经验来解释因子

使用传统集成学习算法预测时序数据的效果

传统的集成学习算法，如随机森林（Random Forest）、梯度提升树（Gradient Boosting Trees, GBM）、XGBoost等，在设计上主要是为了解决非时序数据问题。然而，它们也可以应用于时序数据分析，但效果可能会因以下原因而受限：

• 缺乏对时间序列特性的直接建模能力：这些算法本质上并不考虑输入特征之间的时间顺序，因此不能直接利用时序数据中的自相关性。

• 需要手动特征工程：为了使集成学习算法有效地处理时序数据，通常需要进行大量的预处理工作，包括创建滞后特征、移动平均值、滚动窗口统计量等。这样做可以部分地补偿模型在捕捉时间依赖性方面的不足。

• 性能限制：尽管通过适当的特征工程，集成学习算法可以在某些情况下表现良好，但对于高度动态或者复杂的时间序列（特别是那些包含长期依赖关系的情况），深度学习模型（如LSTM、GRU）或其他专门针对时序数据设计的方法（如ARIMA、Prophet）往往能提供更好的性能。

基于excel的案例

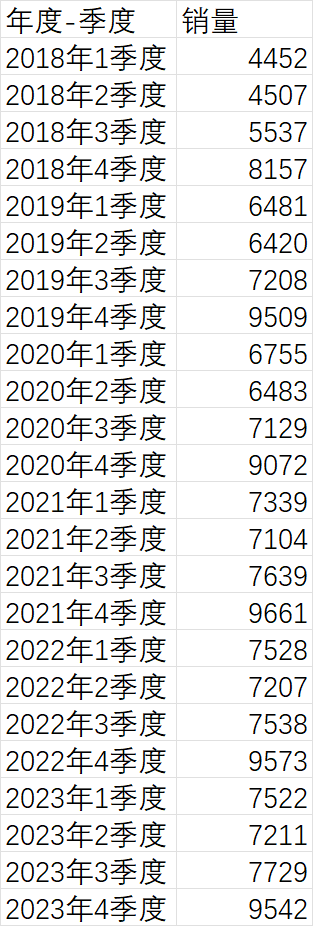
数据如下:

4452
4507
5537
8157
6481
6420
7208
9509
6755
6483
7129
9072
7339
7104
7639
9661
7528
7207
7538
9573
7522
7211
7729
9542

查看数据的折线图

可以看出来数据有一定的季节性与趋势性

构建前一季度和前二季度的特征列

如下

基于前一季度和前二季度的特征列预测当季度销量

选择数据–数据分析–回归–确定

选择Y和X对应的区域

单击确定
可以看R方才0.045不是很好

这里可以看到截距等参数如下

基于参数计算预测值

把参数复制到原始数据表中，新建列为预测值，公式如下

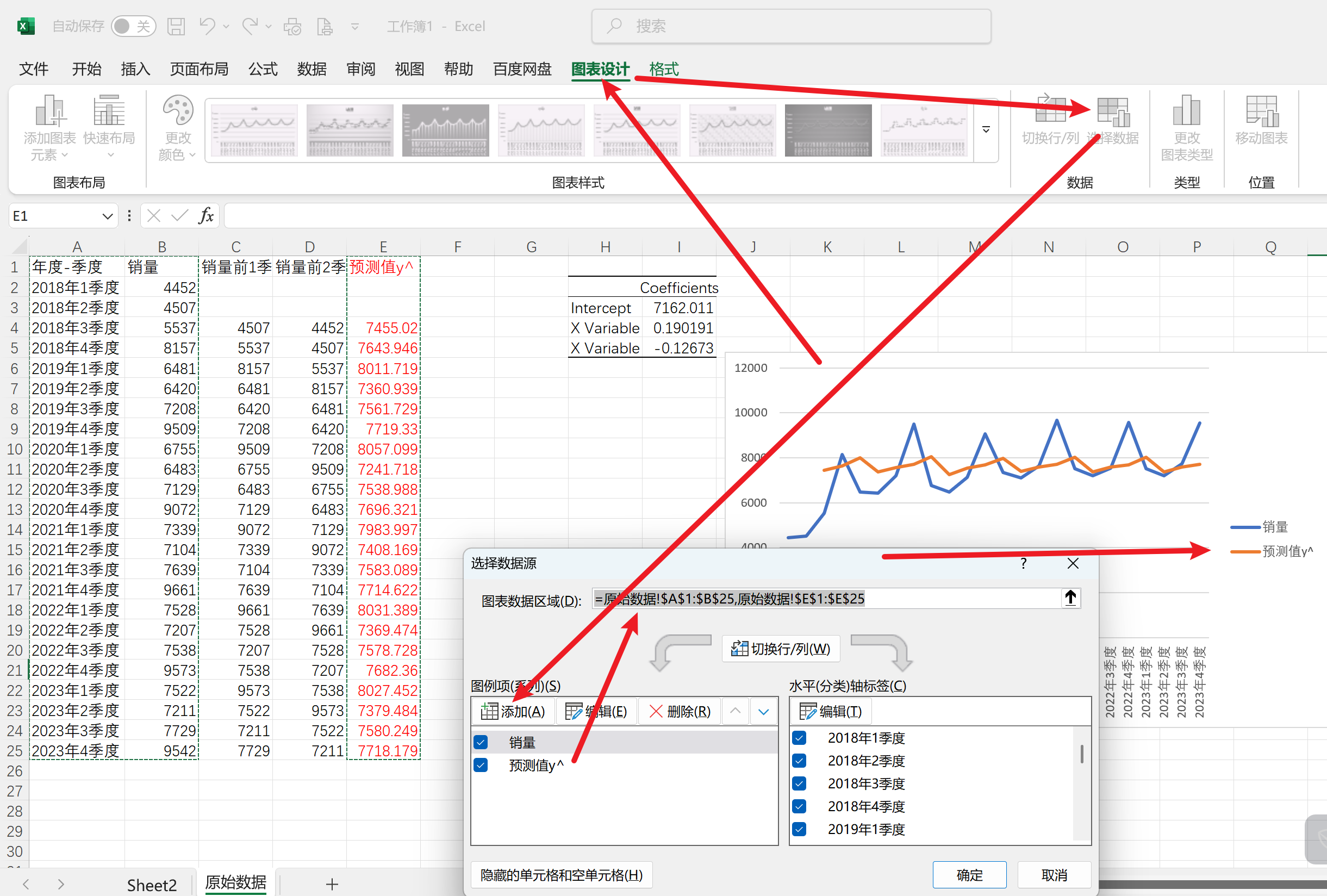
把预测值添加到折线图中
图表–图表设计–添加数据–选择区域–单击确定–生成不同颜色的预测值（在添加图表元素中可以查看）

可以看出效果不是很好

通过差分消除趋势和移动平均消除季节性

把原始数据复制一份，计算一阶差分
再根据一阶差分计算3季度，4季度，5季度的移动平均
可以看到4季度的移动平均基本消除了季节性

基于4个季度移动平均构建前一季度和前二季度的特征列

复制原始数据到移动平均回归新表，复制4个季度移动平均，基于4个季度移动平均列构建前一季度和前二季度特征列，如下

基于新数据进行回归预测

数据-数据分析-回归-选择Y区域和X区域–确定

确定后输出如下：
可以看到R^2的值变为了0.62

基于参数计算预测值

把参数复制过来，带入数据，得到预测值，如下

基于移动平均预测值反推差分值和销量预测值

复制数据到新表，表名为反推销量预测值

创建一阶差分预测值和销量预测值列

把原因的一阶差分和销量值复制过来为初始值

因为预测值为一阶差分四季度移动平均值，顾该处的一阶差分预测值为平均值*4 - 前3个一阶差分和

拖拽公式，完成一阶差分预测值计算

计算销量预测值，销量预测值为一阶差分值+前一个值，如下

这个过程就是ARIMA模型的原理

对比真实值和两种预测结果

把原先回归的预测值和ARIMA预测值 和真实值放在一起，进行折线图绘制 ，选择数据如下

插入折线图

可以看到ARIMA预测的值与真实值比较接近

结论

虽然使用传统的集成学习算法来预测时序数据是可行的，但其效果可能不如专门为时序分析设计的方法好。对于较为简单的时间序列问题，经过恰当的特征工程后，集成学习算法仍能给出不错的预测结果；然而，面对复杂的时序模式，尤其是当数据表现出强烈的周期性或长程依赖时，采用更适合处理时序数据的技术将是更优的选择。

依赖库

依赖包statsmodels

安装依赖包statsmodels

pip install statsmodels==0.14.4

statsmodels` 是一个强大的 Python 库，主要用于统计建模和计量经济学分析。在时间序列分析中，它特别有用，主要功能包括：

1. 统计检验：
   • 如你代码中的 adfuller (ADF检验)，用于检验时间序列的平稳性
   • 其他假设检验（t检验、F检验等）
2. 时间序列分析：
   • 自相关函数（ACF）和偏自相关函数（PACF）计算
   • ARIMA、SARIMA等时间序列模型
   • 状态空间模型
3. 回归分析：
   • 线性回归
   • 广义线性模型
   • 稳健回归
4. 可视化工具：
   • 统计图形绘制（如你代码中的ACF/PACF图）

在你的时间序列分析场景中，statsmodels 提供了完整的工具链：从平稳性检验(ADF) → 自相关分析(ACF/PACF) → 建模(ARIMA等) → 预测。

依赖包torch

pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple

案例

时间序列预测根据过去的模式预测未来事件。我们的目标是找出最佳预测方法，因为不同的技术在特定条件下表现出色。

我们将探讨五种主要方法：

• SARIMAX：检测重复出现的模式并考虑各种外部影响。
• RNN： 分析顺序数据，适用于按时间顺序排列的信息。
• LSTM：通过长时间保留数据来增强 RNN。
• Prophet： 由 Facebook 开发，对数据缺口和重大趋势变化具有强大的抵抗能力。
• Transformer： 利用自我关注，有效识别复杂模式。

我们在不同类型的数据上对这些方法进行了测试：

[1] 电力生产Kaggle 数据集
Electric_Production.csv

[2] 洗发水销售Kaggle 数据集
shampoo_sales.csv

时序数据预测一般方法

数据审查：

首先进行的是对数据趋势的初步评估，通过自相关函数（ACF）和部分自相关函数（PACF）的分析来识别其中的模式。这个步骤对于发现数据中的周期性规律至关重要，能够为后续模型的选择及其参数设定提供依据。

参数调优：

根据所使用的算法以及特定的数据集特性，仔细调整参数以提升预测的精确度。这一过程是确保模型性能的关键步骤。

模型训练与验证：

拆分数据集为训练集验证集和测试集，训练算法，检验模型的有效性和准确性。

效果评估：

采用平均绝对百分比误差（MAPE）作为统一的评价标准，对所有验证数据的表现进行衡量，从而实现不同算法间的直接对比。

此方法不仅有助于深入理解各算法的特性和局限性，还能够指导我们在面对具体的时间序列预测问题时，做出更为明智的算法选择。

电力数据-数据审查

我们使用 “电力生产 ”数据集探索时间序列识别。我们的目标是计算该数据的月平均值，从而发现准确预测所必需的关键趋势和模式。

下面的 Python 脚本将对月度数据汇总进行处理和可视化：

import matplotlib.pyplot as plt
import pandas as pd

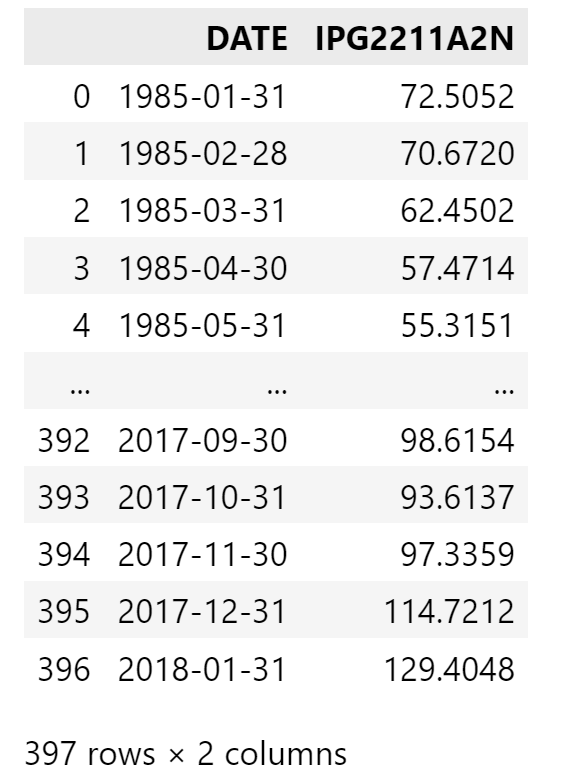
data = pd.read_csv("Electric_Production.csv")
data.info()
data

输出如下：

转换数据类型

#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
data.info()
data

输出如下：

绘制电力数据分布

# data.IPG2211A2N的作用是将数据按照月为单位进行重采样，然后计算每个月的平均值。
# 最后，使用plot()函数将重采样后的数据绘制为折线图。
# ME表示月的结尾，即每个月的最后一天。
# 例如，如果数据的时间范围是2010年1月1日到2020年12月31日，
# 那么重采样后的数据将包含2010年1月到2020年12月的每个月的平均值。
monthly_data = data.IPG2211A2N.resample('ME').mean()
data.IPG2211A2N.resample('ME').mean().plot()
plt.show()

输出如下：

该图（图 1）揭示了电力生产的潜在季节性变化，这对预测工作至关重要。

为了评估数据集的静态性并探索自回归和移动平均成分，我们进行了统计测试和分析，如 Dickey-Fuller 检验、自相关函数 (ACF) 和偏自相关函数 (PACF)：

from statsmodels.tsa.stattools import adfuller, acf, pacf

# 假设 monthly_data 是你的时间序列数据
# Dickey-Fuller test 的意思是：
# 1. 首先，我们需要对时间序列数据进行平稳性检验。
# 2. 平稳性检验的目的是判断时间序列数据是否具有单位根，即是否存在自相关性。
# 3. 单位根的存在意味着时间序列数据不是平稳的，即存在趋势或季节性。
# 4. 平稳性检验的方法是使用 Dickey-Fuller 检验。
# 5. Dickey-Fuller 检验的原理是：
#    1. 首先，我们需要对时间序列数据进行差分。
#    2. 然后，我们需要对差分后的数据进行平稳性检验。平稳性检验的目的是判断时间序列数据是否具有单位根，即是否存在自相关性。 单位根的存在意味着时间序列数据不是平稳的，即存在趋势或季节性。
#    3. 如果差分后的数据是平稳的，那么原始时间序列数据也是平稳的。
#    4. 如果差分后的数据不是平稳的，那么原始时间序列数据也不是平稳的。
# 6. 因此，我们可以使用 Dickey-Fuller 检验来判断时间序列数据是否具有单位根。
# 7. 如果时间序列数据具有单位根，那么我们可以使用 ARIMA 模型来进行预测。
# 8. 如果时间序列数据不具有单位根，那么我们可以使用 ARMA 模型来进行预测。

"""
ADF的中文含义是：
ADF Statistic: -2.25699035004725 # 这个值越小，说明时间序列数据越平稳
p-value: 0.18621469116586592 # 这个值越小，说明时间序列数据越平稳
如果 ADF Statistic 小于临界值，并且 p-value 小于 0.05，那么我们可以认为时间序列数据是平稳的。
如果 ADF Statistic 大于临界值，并且 p-value 大于 0.05，那么我们可以认为时间序列数据不是平稳的。
"""

result = adfuller(monthly_data)
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')

输出如下：

ADF Statistic: -2.25699035004725

p-value: 0.18621469116586592

输出ACF和PACF

# ACF and PACF
acf_values = acf(monthly_data, nlags=20)
pacf_values = pacf(monthly_data, nlags=20, method='ols')
# print ACF and PACF
print("ACF values:", acf_values)
print("PACF values:", pacf_values)

输出如下

ACF values: [1. 0.86277906 0.63640377 0.52487459 0.61398953 0.8028675 0.88986545 0.78414523 0.58354441 0.488432 0.5944013 0.7975361 0.90427102 0.7819278 0.56651747 0.46030659 0.55354872 0.73918453 0.82055665 0.7169618 0.52063329]

PACF values: [ 1. 0.87824247 -0.47155784 0.61231867 0.57390709 0.44843605 0.08025808 -0.07429707 -0.13776652 0.19178424 0.3639721 0.47006531 0.45728639 -0.32745944 -0.01895411 -0.13384899 0.169511 0.07304471 0.01284553 0.0627973 -0.04673421]

可视化ACF和PACF

# ACF and PACF
acf_values = acf(monthly_data, nlags=20)
pacf_values = pacf(monthly_data, nlags=20, method='ols')

# Visualization
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.plot(acf_values)
plt.title('Autocorrelation Function')
plt.subplot(122)
plt.plot(pacf_values)
plt.title('Partial Autocorrelation Function')
plt.tight_layout()
plt.show()

输出如下：

这些分析提供了以下结果：

• Dickey-Fuller 检验： 显示非平稳性，表明需要进行差分。
• ACF 和 PACF： 突显了自回归和移动平均成分的必要性，建议使用初始 ARIMA（1,1,0）模型。

这些发现使我们能够准确地准备和评估各种数据集，以便进行时间序列预测。

电力数据-预测技术

利用 SARIMAX 进行时间序列预测

确定数据集的 ARIMA 模型参数后，我们就可以使用 SARIMAX 进行预测了。SARIMAX 代表带有外生因素的季节性自回归整合移动平均模型，通过纳入季节周期和外部变量的潜在影响来增强 ARIMA。

下面是将 SARIMAX 应用于 “电力生产” 数据集的 Python 示例，其中保留了最近三个月的数据以进行验证：

import pandas as pd
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.arima.model import ARIMA

data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

输出如下：

预测

from sklearn.metrics import mean_absolute_percentage_error
# 将数据分成训练集和测试集

train_data = monthly_data['IPG2211A2N'][:-3]
test_data = monthly_data['IPG2211A2N'][-3:]

# 拟合 ARIMA(1,1,1) 模型
model = ARIMA(train_data, order=(1,1,1))
model_fit = model.fit()

# 预测过去三个月
forecast = model_fit.forecast(steps=3)
# 计算实际值和预测值之间的 MAPE
mape = mean_absolute_percentage_error(test_data, forecast)
print(f"Forecast: {forecast}")
print(f"Actual: {test_data}")
print(f"MAPE: {mape}")

输出如下：

我们使用平均绝对百分比误差 (MAPE) 作为评估预测准确性的指标。同样的方法可应用于其他数据集，从而确保我们预测方法的一致性。

使用 ARIMA 修改为使用 SARIMAX

要将上述代码从使用 ARIMA 修改为使用 SARIMAX，需要对模型的定义和拟合部分进行调整。以下是修改后的代码：

from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.statespace.sarimax import SARIMAX

# 将数据分成训练集和测试集
train_data = monthly_data['IPG2211A2N'][:-3]
test_data = monthly_data['IPG2211A2N'][-3:]

# 拟合 SARIMAX(1,1,1) 模型
model = SARIMAX(train_data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))
model_fit = model.fit()

# 预测过去三个月
forecast = model_fit.forecast(steps=3)

# 计算实际值和预测值之间的 MAPE
mape = mean_absolute_percentage_error(test_data, forecast)
print(f"Forecast: {forecast}")
print(f"Actual: {test_data}")
print(f"MAPE: {mape}")

主要修改点：

1. 导入 SARIMAX：从 statsmodels.tsa.statespace.sarimax 导入 SARIMAX。
2. 替换 ARIMA 为 SARIMAX：将 ARIMA 替换为 SARIMAX。
   • order=(1, 1, 1) 表示非季节性部分的 (p, d, q) 参数。
   • seasonal_order=(0, 0, 0, 0) 表示没有季节性成分（如果需要季节性成分，可以调整这些参数）。
3. 保持其他逻辑不变：包括数据分割、预测和 MAPE 计算。

注意事项：

• 如果你的数据具有季节性模式，可以调整 seasonal_order 参数。例如，如果数据具有 12 个月的季节性周期，可以设置 seasonal_order=(1, 0, 1, 12)。
• SARIMAX 是 ARIMA 的扩展版本，支持更复杂的建模需求，如外生变量和季节性成分。

利用 RNN 进行时间序列预测

递归神经网络（RNN）在时间序列预测中表现突出，因为它能通过隐藏状态动态记忆过去的信息。这与 SARIMAX 的线性建模方法形成鲜明对比，因为 RNN 可以以非线性方式对数据进行建模，使其在理解和预测随时间变化的模式方面表现出色。

下面，我们使用 RNN 对 “电力生产” 数据集进行预测，特别是针对过去三个月的数据进行验证，以评估模型的预测性能。

导入库并加载数据

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

输出如下：

数据探索

查看数据的趋势

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

输出如下：

查看趋势 (Trend)、季节性 (Seasonality) 和 残差 (Residual)。

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

输出如下：

seasonal_decompose() 是 statsmodels 中用于时间序列分解的工具，它将时间序列分解为三个主要成分：趋势 (Trend)、季节性 (Seasonality) 和 残差 (Residual)。通过调用 .plot() 方法，可以生成这些成分的可视化图表。

以下是分解图的解读方法：

---

1. 原始数据 (Observed)

• 这是输入的时间序列数据，表示实际观测值。
• 观察这部分可以帮助你了解数据的整体变化趋势和波动情况。
• 如果数据有明显的周期性或长期趋势，可以在这一部分初步观察到。

---

2. 趋势 (Trend)

• 趋势部分反映了时间序列中的长期变化模式。
• 它通常是通过平滑技术（如移动平均）提取出来的。
• 如何看：
  • 如果趋势线向上倾斜，说明数据有增长趋势。
  • 如果趋势线向下倾斜，说明数据有下降趋势。
  • 如果趋势线接近水平，说明数据没有明显的长期趋势。

---

3. 季节性 (Seasonality)

• 季节性部分反映了时间序列中的周期性波动。
• 它通常是通过从数据中去除趋势和残差后提取出来的。
• 如何看：
  • 如果季节性成分呈现周期性的波形（如正弦曲线），说明数据具有季节性模式。
  • 波动的周期长度可以反映季节性的时间跨度（例如，12个月的周期可能表示年度季节性）。
  • 如果季节性成分接近一条直线（没有明显波动），说明数据可能没有显著的季节性。

---

4. 残差 (Residual)

• 残差部分是原始数据减去趋势和季节性后的剩余部分。
• 它反映了模型无法解释的随机噪声或异常波动。
• 如何看：
  • 如果残差在零附近随机波动且幅度较小，说明模型对数据的拟合较好。
  • 如果残差中存在明显的模式（如趋势或周期性），说明模型可能没有完全捕捉到数据的趋势或季节性。
  • 如果残差的波动幅度较大，说明数据中可能存在更多的噪声或异常值。

---

示例解读

假设你有一个月度销售数据的时间序列，使用 seasonal_decompose().plot() 得到以下结果：

1. Observed: 数据整体呈上升趋势，并且每年的某些月份（如12月）有明显的高峰。
2. Trend: 趋势线显示销售数据逐年增长。
3. Seasonality: 季节性成分显示每年的12月有显著的高峰，而其他月份相对平稳。
4. Residual: 残差部分在零附近随机波动，但偶尔有一些较大的异常值，可能对应特殊事件（如促销活动）。

---

注意事项

1. 分解方法的选择：

   • seasonal_decompose() 默认使用加法分解 (model='additive')，即假设时间序列是由趋势、季节性和残差相加而成。

   • 如果数据的季节性波动随趋势增大而增大，可以选择乘法分解 (model='multiplicative')。

   • 代码示例：

     from statsmodels.tsa.seasonal import seasonal_decompose
     result = seasonal_decompose(data, model='multiplicative', period=12)
     result.plot()
     

2. 周期参数 (period)：

   • period 参数指定了季节性周期的长度。例如，月度数据通常设置为 12（一年12个月），每日数据可能设置为 7（一周7天）。
   • 如果未指定 period，可能会导致分解失败或结果不准确。

3. 残差分析：

   • 残差应该接近白噪声（随机分布）。如果残差中仍有模式，可能需要更复杂的模型（如 SARIMA）来捕捉剩余的结构。

---

通过以上步骤，你可以全面理解时间序列的特性，并为进一步建模（如 ARIMA 或 SARIMAX）提供依据。

数据处理

分解以去除季节性成分并查看

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

输出如下：

对数据进行归一化处理

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

输出如下：

将数据转换为序列

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

输出如下：

拆分数据集并转换数据

拆分训练集和测试集

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

输出如下：

(381, 12, 1) (3, 12, 1) (381, 1) (3, 1)

把数据转换为tensor

# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)

输出如下：

torch.Size([381, 12, 1]) torch.Size([381])
torch.Size([3, 12, 1]) torch.Size([3])

定义一个RNN模型

class SimpleRNN(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(SimpleRNN, self).__init__()
        self.hidden_layer_size = hidden_layer_size
        self.rnn = nn.RNN(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
        predictions = self.linear(rnn_out.view(len(input_seq), -1))
        return predictions[-1]

model = SimpleRNN()
criterion = nn.MSELoss()

optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

训练模型

# 训练模型
epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')

输出如下

评估模型

# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')

输出如下：

Predicted: 0.6018507480621338, Actual: 0.5403230786323547
Predicted: 0.6018507480621338, Actual: 0.5707471966743469
Predicted: 0.6018507480621338, Actual: 0.7388026118278503

计算MAPE的值

# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

输出如下:

MAPE: 2.1545194169134567%

以下是简化代码概述：

• 预处理： 调整季节性并规范化数据，为 RNN 做准备。
• 序列准备： 将数据转换为序列，用于 RNN 训练，模拟时间依赖关系。
• RNN 架构： 利用 RNN 层进行时间处理，利用线性层进行预测。
• 训练： 在历时上迭代以最小化损失，并通过反向传播更新模型。
• 预测： 应用所学模式预测测试集的未来值。
• 反变换： 将预测值调整回原始比例，以供评估。
• 准确度评估： 采用 MAPE 量化模型的预测准确性。

完整代码

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)


# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)


# define RNN
class SimpleRNN(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(SimpleRNN, self).__init__()
        self.hidden_layer_size = hidden_layer_size
        self.rnn = nn.RNN(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
        predictions = self.linear(rnn_out.view(len(input_seq), -1))
        return predictions[-1]

model = SimpleRNN()
criterion = nn.MSELoss()

optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

# 训练模型
epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')


# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')


# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

利用 LSTM 进行时间序列预测

长短期记忆（LSTM）网络旨在通过更好地管理长期依赖性和异常值来改进递归神经网络（RNN）。然而，LSTM 的真正功效因数据集而异，这凸显了经验验证的必要性。在即将对 “电力生产 ”等数据集进行的研究中，我们的目标是对不同算法进行数据驱动的评估，纯粹关注经验结果而非理论预期。以下是为 LSTM 量身定制的 Python 代码示例：

定义LSTM模型

# 定义LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(LSTMModel, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1))
        predictions = self.linear(lstm_out.view(len(input_seq), -1))
        return predictions[-1]

model = LSTMModel()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 180

LSTM完整代码

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)


# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)



# 定义LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(LSTMModel, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1))
        predictions = self.linear(lstm_out.view(len(input_seq), -1))
        return predictions[-1]

model = LSTMModel()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 180

# # define RNN
# class SimpleRNN(nn.Module):
#     def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
#         super(SimpleRNN, self).__init__()
#         self.hidden_layer_size = hidden_layer_size
#         self.rnn = nn.RNN(input_size, hidden_layer_size)
#         self.linear = nn.Linear(hidden_layer_size, output_size)
    
#     def forward(self, input_seq):
#         rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
#         predictions = self.linear(rnn_out.view(len(input_seq), -1))
#         return predictions[-1]

# model = SimpleRNN()
# criterion = nn.MSELoss()

# optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

# # 训练模型
# epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')


# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')


# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

输出如下：

还有类似的方法，就不再演示了，参考的区别如下

数据集：

[1] 电力生产Kaggle 数据集: https://www.kaggle.com/datasets/shenba/time-series-datasets?select=Electric_Production.csv

Electric_Production.csv

[2] 洗发水销售Kaggle 数据集: https://www.kaggle.com/datasets/redwankarimsony/shampoo-saled-dataset

shampoo_sales.csv