Finesse：Fine-Grained Feature Locality based Fast Resemblance Detection for Post-Deduplication Delta

《Finesse：基于细粒度特征局部性的快速相似性检测方法》摘要该论文提出了一种名为Finesse的新型相似性检测方法，用于解决后去重增量压缩中的计算瓶颈问题。针对现有N-transformSF方法计算开销大的问题（需对每个指纹进行N次线性变换），Finesse创新性地利用备份数据中存在的细粒度特征局部性特性，将数据块划分为子块并仅提取最大值特征，完全避免了N次变换。实验表明，Finesse在保

2301_79718870

912人浏览 · 2025-07-23 23:21:59

2301_79718870 · 2025-07-23 23:21:59 发布

关键词

1.背景（background）

数据去重（Deduplication-Dedup）

增量压缩（Delta Compression）

相似性检测（Resemblance Detection）

2.动机（Motivation）

N-transform SF的性能瓶颈：

机会：细粒度局部性（Fine-Grained Feature Locality）

3.创新点（Innovation）

核心思想：Finesse(Fine-Grained Feature Locality based Fast Resemblance Detection)

主要结果 (Table 3, Fig 4, Fig 5)

5.个人启发&联系

1.局部性原理（locality Principle）的威力

2.分治思想（Divide-and-Conquer）的实践

3.计算vs.存储/传输的权衡（Compute vs.Storage/bandwidth Trade-off）

6.总结

链接直达：https://www.usenix.org/system/files/fast19-zhang.pdf

这个标题限制字数，标题全称为研读《Finesse：Fine-Grained Feature Locality based Fast Resemblance Detection for Post-Deduplication Delta Compression》

关键词

主要是三个关键词：

Fine-Grained Feature Locality：细粒度特征局部性
Fast Resemblance Detection 快速相似度检测
Post-Deduplication Delta Compression 重复数据的增量压缩

本文中作者提出的新策略 Finesse

1.背景（background）

核心问题：数据爆炸式增长带来的存储和传输成本上涨

现有的技术：

数据去重（Deduplication-Dedup）

字面意思，识别并消除完全相同的数据块（例如8KB大小）。首先通过计算块的安全哈希值（Rabin Fingerprinting）作为唯一标识，（例如数据库中每条记录的主键，或是人的手上的指纹)，然后比较这些hash值，重复块只需要存储一份，其他的引用它即可，即其他的存储的是指向第一份的存储地址的指针。这样可大幅度节省存储空间和传输带宽。

增量压缩（Delta Compression）

简单来说就是，识别并压缩高度相似但不完全相同的数据块。有些数据虽然不完全相同，但是这些数据之间的内容大部分相同，即高度相似，那么可以存储或传输目标块与一个“基础块”之间的差异（Delta）以及映射关系即可，就不用存储整个目标块了。这是一种冗余数据去重的补充技术，可以进一步挖掘冗余。

相似性检测（Resemblance Detection）

基础步骤，增量压缩的关键第一步。就像医生开药首先要进行检查。相似性检测就需要块准狠地找到哪些非重复块之间是高度相似的，以便后续进行增量编码。这一步的效率是直接影响整个系统的吞吐量的。

现有的相似检测方法-N-transform Super-Feature(N-transform SF):

基于文中Broder定理和Minhash思想

方法：可以快速估算两个集合的相似度

Minhash 最小hash ，快速估算多个集合之间的相似度，某集合（某一列）的最小Hash值等于打乱后这一列第一个值为1的行所在的行号

具体内容可以看这个博客文本相似度算法之-minhash

对数据块计算Rabin指纹（一种滑动窗口hash，CDC,即基于内容的分块）

对每个Rabin指纹进行N次不同的线性变换（M-i*Rabin_j+a_i mod 2^32）

在N个维度上各取一个最大值作为该块的N个特征（Features）

将N个特征分组（例如每K个一组）计算hash得到超级特征（Super-feature,SFs）

两个块共享一个SF，则认为它们高度相似

2.动机（Motivation）

N-transform SF的性能瓶颈：

作者观察到，N-transform SF方法计算开销巨大，成为增量压缩流程的瓶颈。

计算密集：需要对数据块的每个字节位置计算Rabin指纹（滑动窗口）

N倍放大：对每个Rabin指纹，需要进行N次线性变换（乘法+加法+模运算+条件分支比较）

来生成N个特征。结果就是，使得在处理海量数据时开销显著

机会：细粒度局部性（Fine-Grained Feature Locality）

由作者观察到，在备份流等场景中，高度相似的数据块之间，不仅整体相似，其内部的对应子区域（子块，subchunk）也极大概率高度相似，并且顺序一致。

这就意味着，子块的特征（eg.基于子块内容计算的最大值）在相似块之间也有极大概率是相同的。

在这种子块级别的特征重复性即称为“细粒度特征局部性”。

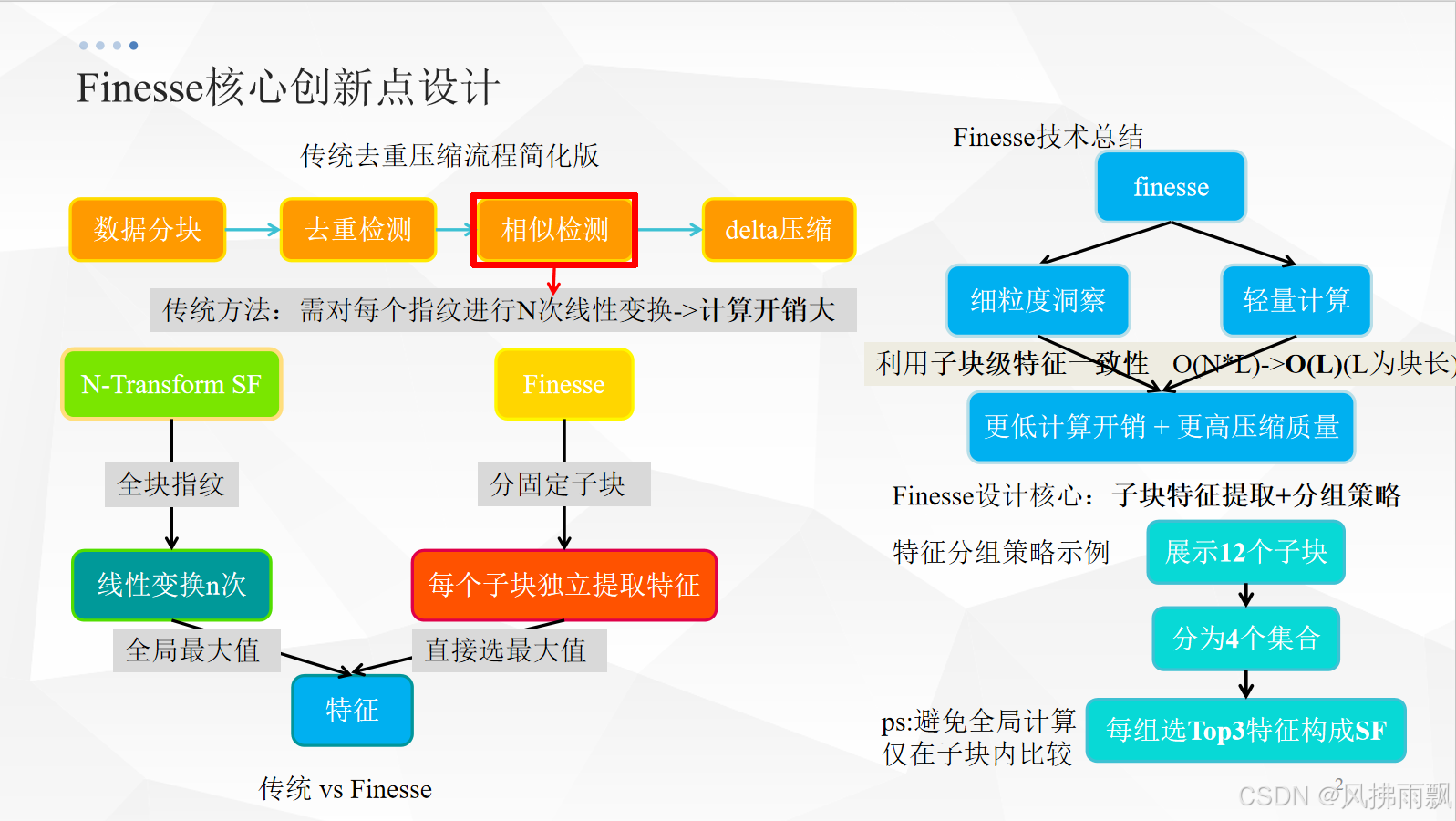
3.创新点（Innovation）

核心思想：Finesse(Fine-Grained Feature Locality based Fast Resemblance Detection)

--利用观察到的“细粒度特征局部性”来避免N-transform SF昂贵的N次线性变换，从而来大幅加速相似检测。

关键方法：

1. 分块（chunk division）将每个数据块固定大小地分割成M个子块（例如8KB块分成12个大约667B子块）

2. 子块特征提取（Subchunk Feature Extraction）对每个子块独立地：

计算该子块内所有Rabin指纹（滑动窗口）

仅需一次操作：找出该子块所有Rabin指纹中的最大值（Max(Rabin_j)）,这就是该子块的特征！省去了N次线性变换

3.特征分组（Feature Grouping）：将M个子块特征分组形成超级特征（SFs）,论文中采用一种跨子块排序分组策略：

将M个子块特征分成若干个连续的组（eg.12个特征分成4个组，则每组3个）

对每组内的特征排序

SF0=所有组的最大值集合（eg.{Goup1_Max,Group2_Max,Group3_Max,Group4_max}）

SF1=所有组的次大值集合 （eg.{Group1_SecondMax,Group2_SecondMax,…}）

SF2=所有组的第三大值集合（eg.{Group1_ThirdMax,Group2_ThirdMax,…}）

本质创新：

就是将特征提取的计算单元从整个数据块的每个字节位置转移到了固定大小的子块。利用局部性，每个子块只需要计算一个特征（最大值），避免N次线性变换，计算量大幅下降。

N-transform SF伪代码

c++代码

// N-transform SF实现
vector<uint32_t> ntransform_sf(const char *block, size_t len)
{ // 计算子块
    // 1. 计算Rabin指纹
    auto fps = compute_rabin_fingerprints(block, len); // 获取指纹列表vector

    if (fps.empty())
        return {}; // 指纹列表为空，返回空

    // 2. 计算特征
    vector<uint32_t> features(NUM_FEATURES, 0); // 以12个特征初始化一个vector，初始值为0

    for (int i = 0; i < NUM_FEATURES; i++)
    { // 遍历每个特征
        uint32_t max_val = 0;
        auto [m, a] = ntransform_constants[i]; // 获取随机数，12对a和b

        // 遍历指纹列表，计算特征
        for (auto fp : fps)
        {                                              // 遍历指纹列表中的每个指纹
            uint32_t transformed = (m * fp + a) & MOD; // 对指纹进行变换，就是乘以一个随机数，然后加上一个随机数
            if (transformed > max_val)
                max_val = transformed; // 更新特征的最大值
        }
        features[i] = max_val; // 将这个最大值存储到特征列表中
    }

    // 3. 生成SF (3个SF，每个由4个特征组成)
    vector<uint32_t> sfs; // 三组，每组四个
    for (int i = 0; i < NUM_SFS; i++)
    { // 3个SF
        uint32_t sf_fp = 0;
        for (int j = 0; j < FEATURES_PER_SF; j++)
        {
            int idx = i * FEATURES_PER_SF + j; //sf的编号乘以4+组内编号，求偏移量
            for (int k = 0; k < 4; k++)
            {
                uint8_t byte = (features[idx] >> (k * 8)) & 0xFF; // 每个数按字节拆分为 “BASE 进制的加权组合”，再将这些组合结果相加
                sf_fp = (sf_fp * BASE + byte) & MOD;              
            }
        }
        sfs.push_back(sf_fp); // 将该块的SF指纹添加到sfs列表中
    }

    return sfs; // 返回SF指纹列表，每个SF指纹是一个uint32_t类型的值
}

Finesse伪代码

Finesse代码

// Finesse实现
vector<uint32_t> finesse(const char *block, size_t len)
{
    // 1. 将块划分为子块
    int num_subchunks = ceil(static_cast<double>(len)/  SUBCHUNK_SIZE);
    vector<uint32_t> features; //存储每个子块的特征值 subchunk_size==8195/12=682字节12个特征
    
    // 2. 处理每个子块
    for (int i = 0; i < num_subchunks; i++)
    {                                                      // 遍历每个子块
        const char *sub_start = block + i * SUBCHUNK_SIZE; // 计算子块起始位置
        size_t sub_len = (i == num_subchunks - 1)
                             ? len - i * SUBCHUNK_SIZE
                             : SUBCHUNK_SIZE; // 计算子块长度，最后一个子块可能小于SUBCHUNK_SIZE

        if (sub_len < WINDOW_SIZE)
        { // 如果子块长度小于窗口大小，跳过
            features.push_back(0);
            cout<<i<<" 小窗 "<<features.size()<<"\n"; // 输出特征数量
            continue;
        }

        // 计算子块指纹
        auto sub_fps = compute_rabin_fingerprints(sub_start, sub_len); // 计算子块的指纹
        // 计算子块特征
        uint32_t max_val = 0; // 初始化最大值为0
        for (auto fp : sub_fps)
        {
            uint32_t transformed = (finesse_m * fp + finesse_a) & MOD; 
            // 对指纹进行线性变换一次
            if (transformed > max_val)
                max_val = transformed; // 子块的指纹作为特征值，更新最大值
        }
        features.push_back(max_val);
    }
    // 3. 特征分组策略 (4组，每组3个特征)
    const int NUM_GROUPS = 4;
    vector<vector<uint32_t>> groups(NUM_GROUPS);
    // 分配特征到组
    for (int i = 0; i < features.size(); i++)
    {
        groups[i % NUM_GROUPS].push_back(features[i]);
    }
    
    // 每组排序
    for (auto &group : groups)
    {
        sort(group.begin(), group.end());
    }

    // 4. 生成SF (3个SF)
    vector<uint32_t> sfs;
    cout<<"Num_SFS: "<<NUM_SFS<<"\n"; // 输出SF的数量
    for (int rank = 0; rank < NUM_SFS; rank++)
    {
        uint32_t sf_fp = 0;
        for (int g = 0; g < NUM_GROUPS; g++)
        {
            // 取每组中第rank大的值 (0=最小, 2=最大)
            int pos = groups[g].size() - 1 - rank; // 第一大，次大，第三大
            if (pos < 0)
                pos = 0;
            uint32_t val = groups[g][pos]; // 获取每组中第rank大的特征值
            cout<<"val"<<val<<"\n"; // 输出特征值
            for (int k = 0; k < 4; k++)
            {
                uint8_t byte = (val >> (k * 8)) & 0xFF;
                sf_fp = (sf_fp * BASE + byte) & MOD;
            }
          
        }
        sfs.push_back(sf_fp);
    }

    return sfs;
}

4.实验 (Evaluation)

目标：验证 Finesse 在压缩率、检测质量、速度、系统吞吐量上相比 N-transform SF 的表现。

平台：基于开源去重系统 Destor 实现增量压缩原型。Intel i7/E5 CPU, HDDs。

配置：典型设置（8KB CDC, SHA1去重, 3 SFs x 4 features/SF, Xdelta编码, LRU基础块缓存）。

数据集： 6种真实备份数据集（WEB-网页快照, TAR-Linux内核源码包, RDB-Redis备份, SYN-合成备份, VMA/VMB-虚拟机镜像）。

关键指标

DCR (Delta Compression Ratio): 压缩前总大小 / 压缩后总大小 - 衡量整体空间节省。

DCE (Delta Compression Efficiency): (压缩后目标块大小) / (压缩前目标块大小) - 衡量检测到的相似块本身的压缩效率（越高说明假阳性越低，相似度越高）。

相似性计算速度 (Similarity Computing Speed): 计算 SFs 的速度 (MB/s)。

系统吞吐量 (System Throughput): 整个系统（去重+增量压缩）处理数据的速度 (MB/s)。

主要结果 (Table 3, Fig 4, Fig 5)

压缩率 (DCR/DCE) 相当或略优： Finesse 的 DCR 与 N-transform SF 相差在 -3.21% ~ +7.36% 之间，DCE 均高于 N-transform SF。说明 Finesse 在保持甚至略微提升检测质量（减少假阳性）的前提下工作。DCE 更高是因为 Finesse 的分组策略强制特征来自不同子块，且避免了检测大小差异过大的“伪相似”块。

速度大幅提升： Finesse 计算 SFs 的速度是 N-transform SF 的 3.2x - 3.5x。核心优势得到验证！计算开销的降低直接体现在这里。（算法复杂度降低 - O(N*L) vs O(M) (L是块字节数，M是子块数，M << L)，流水线效率提升）

系统吞吐量显著提高： 得益于相似性检测速度的提升，整合了 Finesse 的整个（去重+增量压缩）系统的吞吐量比整合 N-transform SF 的系统高出 41% - 85%。瓶颈消除效果明显！

敏感性：性能提升在不同数据集上稳定（速度、吞吐量），压缩率受数据集演化模式影响略有波动（但都在可接受范围内）。

5.个人启发&联系

1.局部性原理（locality Principle）的威力

在CS中是一块重要的基石，

论文：观察并利用了细粒度（子块级）的空间局部性（相似快的对应子块也相似）。（什么是备份流局部性？可以理解为cache的局部性）

就是对块级数据时间/空间局部性的深化

就像Cache设计（多级Cache，行大小）的核心就是利用程序访问的时间局部性和空间局部性来减少访存延迟。还有操作系统中虚拟内存的页面置换算法（如LRU）基于时间局部性

2.分治思想（Divide-and-Conquer）的实践

将大问题分解为小问题独立解决

论文：将整个块的特征计算这个大问题，分解为多个子块的特征计算这些小问题。子块问题更简单（只需要找最大值），且可以利用局部性（子块特征重复性高）

数据结构中，快排，归并排序都是经典的分治策略。

分布式系统：将大任务拆分到多个节点并行处理就是核心思想

3.计算vs.存储/传输的权衡（Compute vs.Storage/bandwidth Trade-off）

论文：N-transform付出高昂的计算代价来获得高质量的SFs以支持增量压缩（节省存储/带宽），而Finesse通过利用数据内在特征（局部性），显著降低了计算开销空间（CPU时间），同时保持了存储和宽带的节省效果，甚至略有提升（DCE）,优化权衡得很好。

6.总结

Finesse 这篇论文的核心贡献在于，敏锐地发现了现有增量压缩相似性检测方法 (N-transform SF) 的计算瓶颈（对每个指纹进行 N 次线性变换），并创造性地利用备份数据中普遍存在的细粒度特征局部性（相似块对应子块也相似），提出了一种分块计算特征最大值的新方法。这种方法完全避免了昂贵的 N 次线性变换，将计算复杂度从 O(N*块大小) 降低到 O(子块个数)，从而实现了 3.2x-3.5x 的特征计算加速 和 41%-85% 的系统吞吐量提升，同时保持了相当的压缩率甚至提升了检测质量（更高的 DCE）。这是一个将 局部性原理、分治思想 应用于解决实际系统性能瓶颈（计算 vs. 存储/带宽权衡）的经典案例。