脉冲多普勒噪声雷达中用于无模糊多普勒估计的子脉冲处理

G. Beltrão, L. Pralon, A. Barreto, M. Alaee-Kerahroodi and M. R. B. Shankar, “Subpulse Processing for Unambiguous Doppler Estimation in Pulse-Doppler Noise Radars,” in IEEE Transactions on Aerospace and Electronic Systems, vol. 57, no. 6, pp. 3813-3826, Dec. 2021, doi: 10.1109/TAES.2021.3088501.

第一章：引言与研究背景

1.1 多普勒困境的本质

在现代雷达系统中，为了估计目标沿雷达视线的相对速度（径向速度），众多应用采用了某种形式的脉冲多普勒处理架构。这包括空中监视、连续波（CW）雷达和超宽带雷达等应用。然而，这种方法不可避免地导致了目标距离和速度同时无模糊估计之间的根本性权衡，这就是著名的多普勒困境（Doppler dilemma）。

这一现象的核心在于：脉冲重复频率（PRF）的选择既决定了最大无模糊距离，又决定了最大无模糊速度，而这两者呈反比关系。具体而言：

• 高PRF能够提供大的无模糊速度范围，但限制了无模糊距离
• 低PRF能够提供大的无模糊距离范围，但限制了无模糊速度

1.2 噪声雷达的特殊挑战

噪声雷达系统使用随机过程的实现作为发射波形。尽管这些系统具有固有的高带宽特性和近似图钉型的模糊函数，但在实际应用中，特别是当时间带宽积存在实际限制时，无模糊的距离和多普勒估计仍然面临重大挑战。主要问题包括：

1. 低多普勒容限：随机波形通常呈现近图钉型模糊函数，导致多普勒容限较低
2. 匹配滤波器损失：快速目标导致的多普勒失配会造成严重的匹配滤波器损失
3. 探测性能下降：对于远程或快速目标应用，噪声雷达的使用仍然受限

第二章：传统脉冲多普勒处理的数学框架

2.1 信号模型

设${\tilde{s}}_i(t)$为雷达在第i个间隔开始时发射的时间受限信号的复包络，其中：

• $i\in [0,n_p-1]$称为"慢时间"索引
• $t\in [0,\text{PRI}]$表示相对于传输开始的时间，称为"快时间"

对于距离$R_0$处的单点移动散射体（在开始被雷达照射时的距离），第i个接收信号的复包络为：

$${\tilde{r}}_i(t)=A{e}^{-j4\pi \frac{R_0+v{T}_i}{\lambda }}{e}^{-j2\pi f_{d}t}{\tilde{s}}_i\left(t-T_0-\frac{2v}{c}{T}_i\right)\text{\hspace{1em}(1)}$$

其中各参数的物理意义为：

• $A$：复数幅度，反映后向散射效应、信道衰落和接收机增益
• $\lambda$：工作波长
• $v$：目标径向速度（假设在CPI内恒定）
• $f_d$：对应的多普勒频率
• $T_0=2R_0/c$：回波信号往返时间
• $T_i=(i-1)\text{PRI}$：第i个脉冲的发射时刻
• $c$：光速

2.2 匹配滤波处理

最大化接收机信噪比（SNR）的操作是匹配滤波。对于脉冲串波形，它简单地是单脉冲匹配滤波器输出的缩放和移位副本的总和。第i个匹配滤波器输出的复包络为：

$${\tilde{y}}_i(t)={\int }_{-\infty }^{\infty }{\tilde{r}}_i(\alpha ){\tilde{s}}_i^{\ast }(\alpha -t)d\alpha \text{\hspace{1em}(2)}$$

将式(1)代入式(2)，并利用脉冲模糊函数的定义：

$${\chi }_{{\tilde{s}}_i}(\tau ,f)={\int }_{-\infty }^{\infty }{\tilde{s}}_i(t){\tilde{s}}_i^{\ast }(t-\tau )e^{j2\pi ft}dt$$

可以将匹配滤波器输出重写为：

$${\tilde{y}}_i(t)=A{e}^{-j4\pi \frac{R_0+v{T}_i}{\lambda }}{\chi }_{{\tilde{s}}_i}\left(t-T_0-\frac{2v}{c}{T}_i,f_d\right)\text{\hspace{1em}(3)}$$

2.3 多普勒困境的量化

系统的最大无模糊距离由PRF决定：

$$R_u=\frac{c\cdot \text{PRI}}{2}\text{\hspace{1em}(4)}$$

而最大无模糊速度为：

$$|v_{pu}|=\frac{\lambda }{4\cdot \text{PRI}}=\frac{\lambda \cdot \text{PRF}}{4}\text{\hspace{1em}(5)}$$

从式(4)和(5)可以看出，$R_u$和$|v_{pu}|$的乘积是一个常数：

$$R_u\cdot |v_{pu}|=\frac{c\lambda }{8}$$

这个恒定的乘积关系正是多普勒困境的数学表达。

第三章：子脉冲多普勒处理架构

3.1 子脉冲分解原理

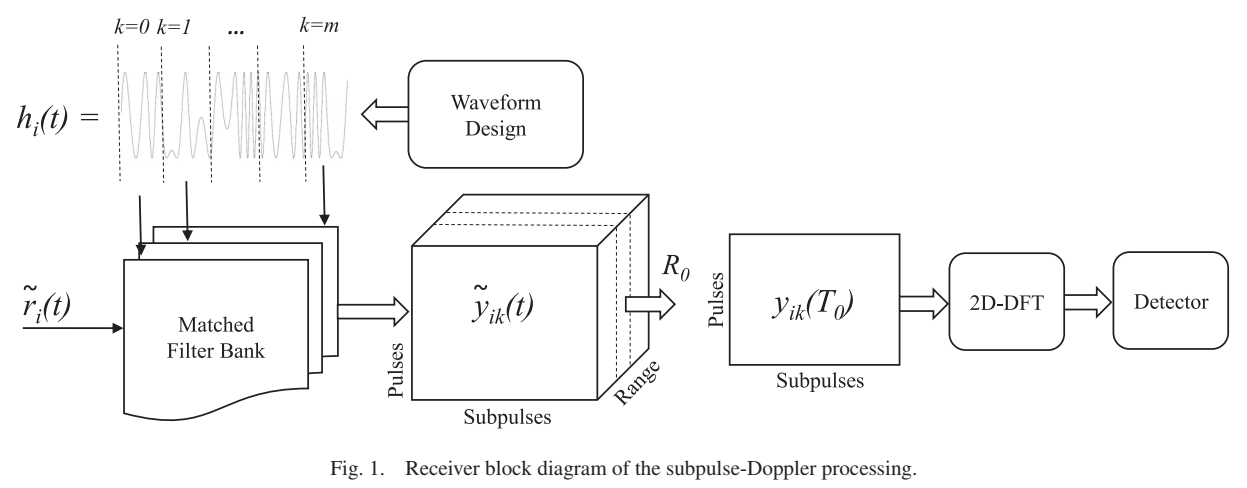
图1：子脉冲多普勒处理的接收机框图
该图展示了完整的处理流程：接收信号首先通过m个并行的匹配滤波器组（每个对应一个子脉冲），然后经过脉冲维度和子脉冲维度的2D-DFT处理，最终送入检测器。

核心创新在于将第i个匹配滤波器参考信号$h_i(t)$划分为m个子脉冲：

$$h_i(t)=\sum _{k=0}^{m-1}{h}_{ik}(t)\text{\hspace{1em}(6)}$$

每个子脉冲定义为：

$$h_{ik}(t)={\tilde{s}}_i(t)\left[u\left(t-{\tau }_s\frac{k}{m}\right)-u\left(t-{\tau }_s\frac{k+1}{m}\right)\right]\text{\hspace{1em}(7)}$$

其中$u(t)$是Heaviside阶跃函数，${\tau }_s$是第i个发射脉冲持续时间。

3.2 子脉冲接收信号模型

基于子脉冲分解，第i个接收信号可以重写为：

$${\tilde{r}}_i(t)=A\sum _{k=0}^{m-1}{e}^{-j4\pi \frac{R_0+v{T}_i}{\lambda }}{e}^{-j2\pi f_{d}t}{h}_{ik}\left(t-T_0-\frac{2v}{c}{T}_{ik}\right)\text{\hspace{1em}(8)}$$

其中$T_{ik}={\tau }_s\frac{k}{m}+T_i$表示第i个脉冲中第k个子脉冲的时间位置。

3.3 子脉冲匹配滤波输出

执行m个匹配滤波操作，每个对应一个子脉冲。第k个匹配滤波器输出的复包络可表示为：

$${\tilde{y}}_{ik}(t)=A{e}^{-j4\pi \frac{R_0+v{T}_{ik}}{\lambda }}{\chi }_{{\tilde{s}}_{ik}}\left(t-T_0-\frac{2v}{c}{T}_{ik},f_d\right)\text{\hspace{1em}(9)}$$

对于噪声雷达，考虑到随机波形的统计特性，期望值为：

$$E[{\tilde{y}}_{ik}(t)]=\frac{{\tau }_s}{m}A{R}_{\tilde{s}}\left(t-T_0-\frac{2v}{c}{T}_{ik}\right)\text{sinc}\left(f_d\frac{{\tau }_s}{m}\right)e^{-j4\pi \frac{R_0+v{T}_{ik}}{\lambda }}\text{\hspace{1em}(13)}$$

其中$R_{\tilde{s}}(\tau )$是随机过程$\tilde{s}(t)$的自相关函数。

3.4 相位分析与速度估计

每个匹配滤波器输出${\tilde{y}}_{ik}(t)$之间的相位是目标径向速度v的线性函数：

$${\theta }_{ik}=\frac{4\pi (R_0+v{T}_{ik})}{\lambda }\text{\hspace{1em}(14)}$$

这种线性相位变化存在于子脉冲(k)和慢时间(i)两个维度，为二维多普勒分析提供了基础。

第四章：二维离散傅里叶变换处理

4.1 脉冲维度DFT

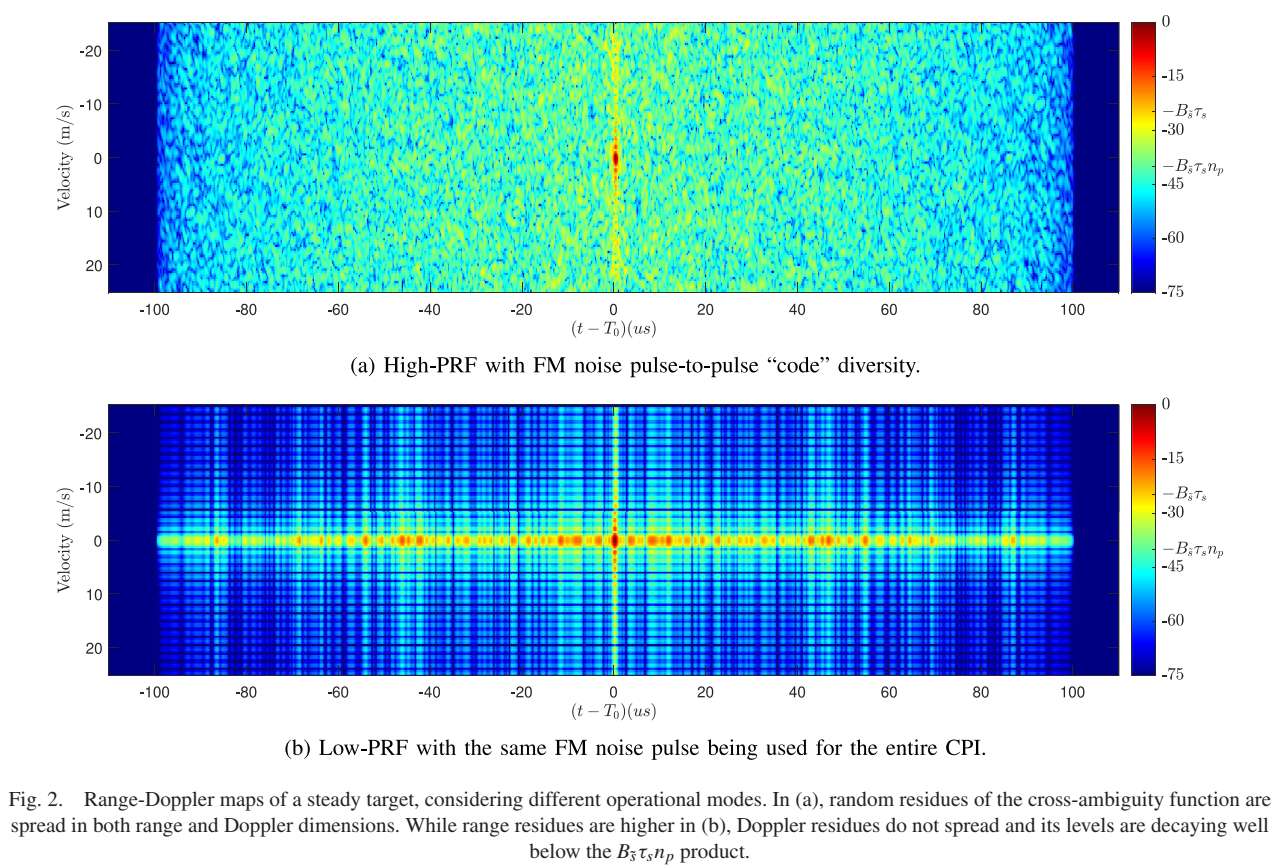
图2：不同操作模式下的距离-多普勒图

• 图2(a)显示了标准噪声雷达操作，具有较高的PRF和脉冲间分集。可以看到交叉模糊函数的随机残余在距离和多普勒维度上扩散，平均值低于主峰$B_{\tilde{s}}{\tau }_s{n}_p=40.08$ dB。
• 图2(b)描述了低PRF操作，整个CPI使用相同的噪声脉冲（无"码"分集）。虽然距离残余较高（低于主峰$B_{\tilde{s}}{\tau }_s=24.77$ dB），但多普勒残余不扩散，其水平衰减远低于$B_{\tilde{s}}{\tau }_s{n}_p$乘积。

对于给定子脉冲k，在快时间瞬间$t=T_0$（目标距离位置），脉冲维度的1D-DFT输出为：

$$E[{\tilde{Y}}_k^{\prime }(f_p)]{|}_{t=T_0}=\frac{{\tau }_s}{m}A{R}_{\tilde{s}}(0)\text{sinc}\left(f_d\frac{{\tau }_s}{m}\right)e^{-j4\pi \frac{R_0+v{T}_k}{\lambda }}{\psi }_p(f_p-f_d)\text{\hspace{1em}(15)}$$

其中混叠sinc函数定义为：

$${\psi }_p(x)=\frac{\sin (\pi x{n}_p\text{PRI})}{\sin (\pi x\text{PRI})}{e}^{-j\pi x(n_p-1)\text{PRI}}\text{\hspace{1em}(16)}$$

4.2 子脉冲维度DFT

类似地，对于给定脉冲i，子脉冲维度的1D-DFT输出为：

$$E[{\tilde{Y}}_i^{\prime }(f_s)]{|}_{t=T_0}=\frac{{\tau }_s}{m}A{R}_{\tilde{s}}(0)\text{sinc}\left(f_d\frac{{\tau }_s}{m}\right)e^{-j4\pi \frac{R_0+v{T}_i}{\lambda }}{\psi }_{sp}(f_s-f_d)\text{\hspace{1em}(17)}$$

其中子脉冲维度的混叠sinc函数为：

$${\psi }_{sp}(x)=\frac{\sin (\pi x{\tau }_s)}{\sin (\pi x{\tau }_s/m)}{e}^{-j\pi x{\tau }_s(m-1)/m}\text{\hspace{1em}(18)}$$

脉冲方向的相干增益为$n_p$（当$f_p=f_d$时），子脉冲方向的相干增益为m（当$f_s=f_d$时），补偿了式(13)中的衰减因子。

第五章：参数选择与系统设计

5.1 无模糊速度扩展

通过子脉冲处理，最大无模糊速度现在变为：

$$|v_{spu}|=\frac{m\lambda }{4{\tau }_s}\text{\hspace{1em}(19)}$$

这与系统PRF无关，提供了设计上的灵活性。所需的子脉冲数m可以计算为：

$$m=\lceil 4{\tau }_s{v}_{max}/\lambda \rceil \text{\hspace{1em}(20)}$$

5.2 唯一解码条件

为了在2D多普勒图上提供唯一解码，必须满足：

$$2|v_{pu}|=\delta v_{sp}\text{\hspace{1em}(22)}$$

其中$\delta v_{sp}=2|v_{spu}|/N_{sp}$是子脉冲维度的离散化（单元大小）。

这导致关键关系：

$$\frac{m}{N_{sp}}=\frac{{\tau }_s}{\text{PRI}}=d_c\text{\hspace{1em}(23)}$$

其中$d_c$是发射机占空比。这个关系确保了脉冲维度中的每个速度折叠与子脉冲维度中的离散化单元重合。

5.3 多普勒分辨率分析

脉冲DFT的多普勒分辨率（3dB宽度）为：

$$\Delta f_p=\frac{0.89}{\text{CPI}}=\frac{0.89}{n_p\text{PRI}}\text{\hspace{1em}(25)}$$

子脉冲多普勒分辨率为：

$$\Delta f_{sp}=\frac{0.89}{{\tau }_s}\text{\hspace{1em}(26)}$$

低子脉冲多普勒分辨率不会降低整体系统性能，因为脉冲分析仍提供精细分辨率。

第六章：仿真结果与性能评估

6.1 二维多普勒图分析

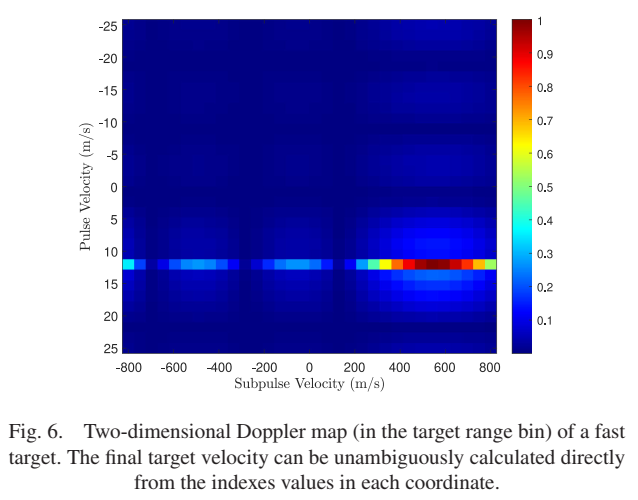
图6：目标距离仓中的二维多普勒图
该图显示了快速目标（511 m/s）的处理结果。可以清楚地看到式(17)和(15)中描述的2D混叠sinc模式，以及子脉冲维度的低分辨率。最终目标速度可以直接从各坐标的索引值计算得出。

6.2 距离剖面比较

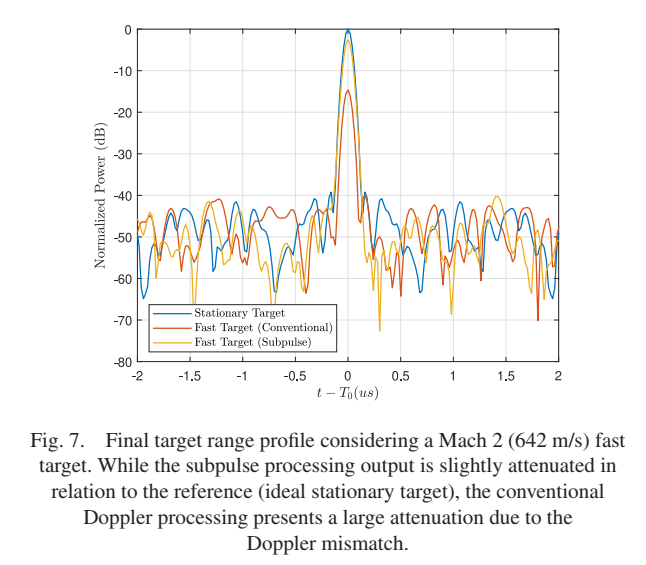
图7：不同序列的最终目标距离剖面
图中比较了传统多普勒处理（蓝线）和子脉冲处理（红线）对于Mach 2（642 m/s）快速目标的输出。传统多普勒处理由于多普勒失配呈现出大的衰减（比理想情况低14.68 dB）。相比之下，子脉冲处理补偿了1/m距离匹配滤波器衰减，其绝对值仅比理论零多普勒情况小2.59 dB，对应于超过12 dB的最终SNR改善。

6.3 估计性能统计

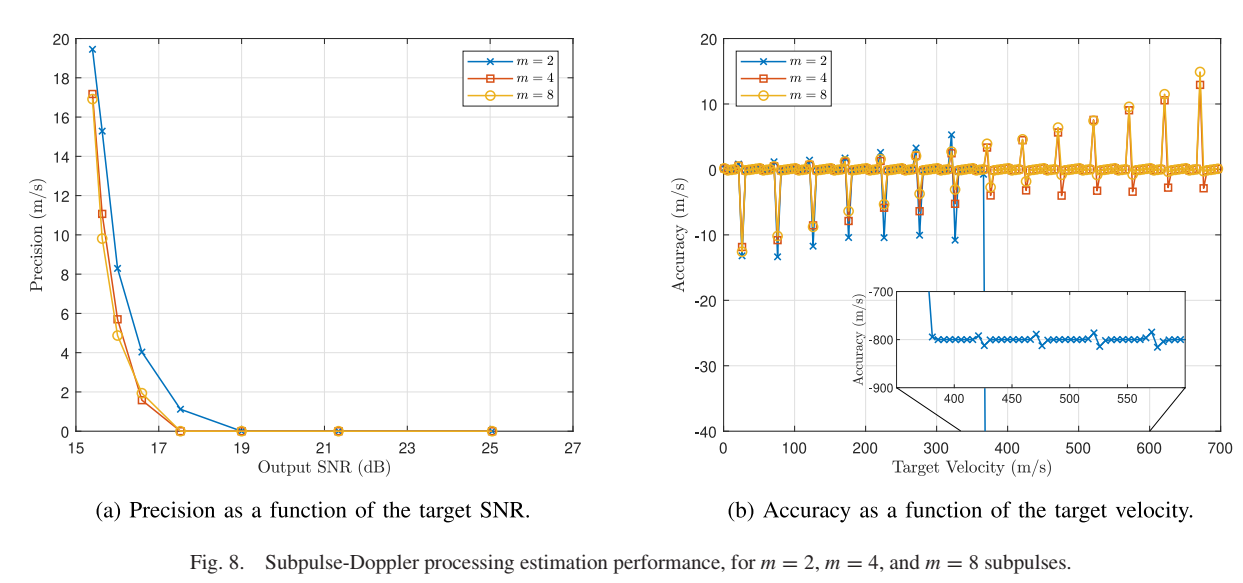
图8：子脉冲多普勒处理估计性能

• 图8(a)显示了精度作为目标SNR的函数（m=2, 4, 8子脉冲）
• 图8(b)显示了准确度作为目标速度的函数

估计的精度定义为：
$${\sigma }_{\hat{\Theta }}=\sqrt{E\left[(\hat{\Theta }-\bar{\hat{\Theta }}{)}^2\right]}\text{\hspace{1em}(33)}$$

准确度定义为：
$$B_{\hat{\Theta }}(\Theta )=E[\hat{\Theta }-\Theta ]\text{\hspace{1em}(34)}$$

6.4 副瓣性能分析

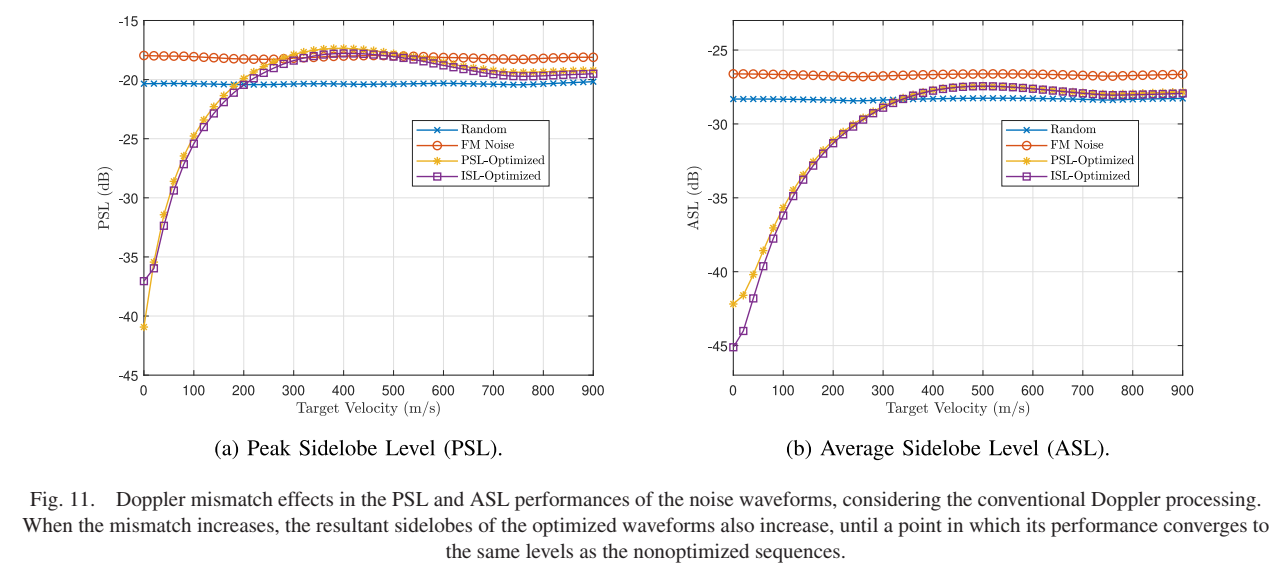
图11：PSL和ASL性能作为目标速度的函数
该图展示了考虑传统多普勒处理时噪声波形的峰值副瓣电平（PSL）和平均副瓣电平（ASL）性能。当失配增加时，优化波形的结果副瓣也增加，直到其性能收敛到与非优化序列相同的水平。

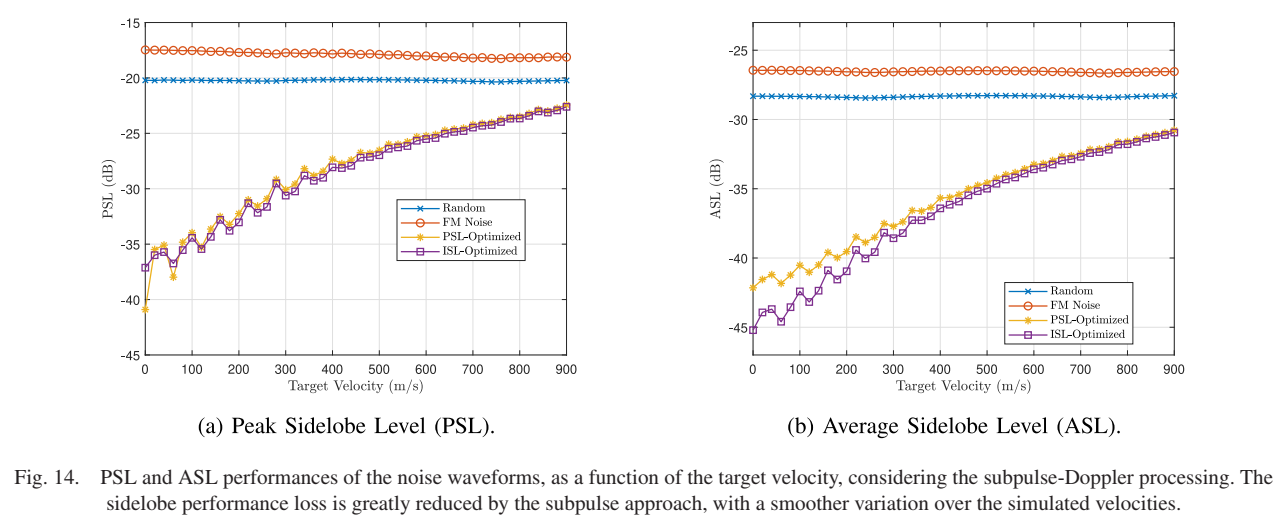
图14：子脉冲多普勒处理的PSL和ASL性能
通过子脉冲方法，副瓣性能损失大大减少，在模拟速度上具有更平滑的变化。这表明子脉冲处理不仅增加了多普勒容限，还提高了优化序列对多普勒失配的鲁棒性。

第七章：实现复杂度分析

7.1 计算复杂度

基于以下假设进行复杂度分析：

1. 大部分计算工作与原始数据处理有关，特别是接收数据的DFT（距离和多普勒）
2. 参考信号的DFT可以预先计算和存储
3. 距离匹配滤波操作使用快速卷积技术执行

子脉冲处理的DFT总数为：

• $m{n}_p$个距离匹配滤波操作，共$2m{n}_p$个大小为$n_{rg}$的DFT
• $m{n}_{rg}$个脉冲维度上大小为$n_p$的DFT
• $n_p{n}_{rg}$个子脉冲维度上大小为m的DFT

计算负载增加比为：

$$\frac{N_{op}^{sub}}{N_{op}^{conv}}=m\left(1+\frac{\log (m)}{\log (n_{rg}^2{n}_p)}\right)\text{\hspace{1em}(27)}$$

7.2 FPGA实现资源消耗

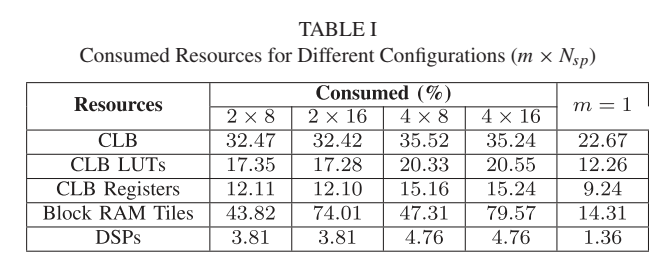
表I：不同配置的资源消耗（$m\times N_{sp}$）

该表显示了在Xilinx Zynq UltraScale+ MPSoC（ZU15EG）设备上的实现结果：

• 对于m=2和m=4子脉冲，CLB资源消耗分别增加约1.4倍和1.6倍
• DSP和Block RAM Tiles增加约2.9倍和3.4倍
• 即使在最苛刻的配置下，总消耗资源也不超过可用容量的80%

附录A：噪声雷达模糊函数的统计分析

A.1 窄带模糊函数推导

对于复随机过程$\tilde{s}(t)$，窄带模糊函数由其集合平均适当描述：

$$E[{\chi }_{\tilde{s}}(\tau ,f_d)]=E\left[{\int }_{-\infty }^{\infty }\tilde{s}(t){\tilde{s}}^{\ast }(t-\tau )e^{j2\pi f_{d}t}dt\right]\text{\hspace{1em}(10)}$$

假设$\tilde{s}(t)$是宽平稳的，可以推导出：

$$E[{\chi }_{\tilde{s}}(\tau ,f_d)]={\tau }_s{R}_{\tilde{s}}(\tau )\text{sinc}(f_d{\tau }_s)\text{\hspace{1em}(11)}$$

其中$R_{\tilde{s}}(\tau )=E[\tilde{s}(t){\tilde{s}}^{\ast }(t-\tau )]$是自相关函数。

A.2 子脉冲模糊函数分析

由于发射信号由宽平稳随机过程表征，任何等间隔采样集具有与整个过程相似的统计特性（可分性）。特别地，任何子脉冲具有与整个脉冲相似的统计特性。

对于子脉冲$k$，其模糊函数的期望值为：

$$E[{\chi }_{{\tilde{s}}_{ik}}(\tau ,f_d)]=\frac{{\tau }_s}{m}{R}_{\tilde{s}}(\tau )\text{sinc}\left(f_d\frac{{\tau }_s}{m}\right)$$

这解释了为什么每个子脉冲保持相同的距离分辨率（由$R_{\tilde{s}}(\tau )$决定），同时提高了多普勒容限（sinc函数参数减小了m倍）。

附录B：波形优化问题的数学表述

B.1 峰值副瓣电平（PSL）优化

设$\mathbf{s}=[s_1,s_2,...,s_N{]}^T\in {\mathbb{C}}^N$为离散发射快时间信号的采样版本，其非周期自相关函数定义为：

$$r_k=\sum _{i=1}^{N-k}{s}_i^{\ast }{s}_{i+k},k=0,...,N-1\text{\hspace{1em}(28)}$$

PSL优化问题表述为：

P1:min⁡smax⁡k=1N−1{∣rk∣}s.t.∣si∣=1,i=1,...,N(31)\begin{aligned} P_1: \quad &\min_{\mathbf{s}} \max_{k=1}^{N-1}\{|r_k|\} \\ &\text{s.t.} \quad |s_i| = 1, \quad i = 1, ..., N \end{aligned} \tag{31}P1​:​smin​k=1maxN−1​{∣rk​∣}s.t.∣si​∣=1,i=1,...,N​(31)

B.2 积分副瓣电平（ISL）优化

ISL定义为：

$$\text{ISL}=\sum _{k=1}^{N-1}|r_k{|}^2=f_2(\mathbf{s})\text{\hspace{1em}(30)}$$

相应的优化问题为：

$$\begin{array}{rl}{P}_2:& \underset{\mathbf{s}}{\min }\sum _{k=1}^{N-1}|r_k{|}^2\\ & \text{s.t.}|s_i|=1,i=1,...,N\end{array}\text{\hspace{1em}(32)}$$

这些是非凸约束多变量问题。采用坐标下降方法，通过求解一系列更简单的单变量最小化子问题来最小化目标函数。

B.3 平均副瓣电平（ASL）

ASL与ISL的关系为：

$$\text{ASL}=\frac{1}{N-1}\sum _{k=1}^{N-1}|r_k{|}^2=\frac{1}{N-1}\text{ISL}\text{\hspace{1em}(35)}$$

对于噪声波形，ASL通常收敛到系统时间带宽积，这决定了可能的掩蔽效应中的噪声底电平（残余波动）。

附录C：二维DFT的详细推导

C.1 从1D到2D变换

考虑匹配滤波器输出矩阵$\mathbf{Y}\in {\mathbb{C}}^{m\times n_p}$，其中元素$Y_{k,i}={\tilde{y}}_{ik}(T_0)$。

二维DFT定义为：

$$\tilde{Y}(f_s,f_p)=\sum _{k=0}^{m-1}\sum _{i=0}^{n_p-1}{Y}_{k,i}{e}^{-j2\pi (k{f}_s/m+i{f}_p/n_p)}$$

将式(13)代入并分离变量：

$$\tilde{Y}(f_s,f_p)=\frac{{\tau }_s}{m}A{R}_{\tilde{s}}(0)\text{sinc}\left(f_d\frac{{\tau }_s}{m}\right)\cdot {\Psi }_{2D}(f_s,f_p,f_d)$$

其中${\Psi }_{2D}$是二维混叠函数。

C.2 速度解码算法

给定2D-DFT输出的峰值位置$(k_s,k_p)$，目标速度计算为：

$$v=v_{sp}+v_p=k_s\cdot \delta v_{sp}+k_p\cdot \delta v_p$$

其中：

• $\delta v_{sp}=2|v_{spu}|/N_{sp}$：子脉冲速度分辨率
• $\delta v_p=2|v_{pu}|/n_p$：脉冲速度分辨率

当满足式(23)的条件时，每个脉冲维度的模糊折叠正好对应子脉冲维度的一个离散单元，确保了唯一解码。