【三维重建】3R-GS：优化相机位姿的3DGS最佳实践

3R-GS提出了一种联合优化3D高斯泼溅(3DGS)与相机位姿的新方法。针对传统3DGS依赖SfM初始位姿的问题，该研究通过整合MCMC采样、MLP全局位姿优化和无渲染几何约束三大创新，显著提升了复杂场景下的重建鲁棒性。实验表明，3R-GS在保持3DGS高效性的同时，实现了更精确的相机位姿估计和更高保真度的视图合成效果。该方法为3D重建与相机标定的联合优化提供了新思路。

杀生丸学AI

825人浏览 · 2025-09-10 23:22:58

杀生丸学AI · 2025-09-10 23:22:58 发布

在这里插入图片描述

标题：<3R-GS: Best Practice in Optimizing Camera Poses Along with 3DGS>
来源：德州农工大学，2香港大学，3香港科技大学
主页：https://zsh523.github.io/3R-GS/

文章目录

摘要
二、相关工作：CF-3DGS（COLMAP-Free 3DGS）
- 2.1 Local 3DGS：估计相对相机位姿
- 2.2 Global 3DGS：逐帧更新构建全局模型
三、主要方法
实验

摘要

3DGS凭借其高效性和高质量表现彻底革新了神经渲染领域，但与许多新型视图合成方法类似，该技术高度依赖结构从运动（SfM）系统提供的精确相机位姿。尽管近期SfM流程取得了显著进展，但如何在复杂场景（如无纹理场景）中同时提升系统鲁棒性与相机参数估计精度的问题仍待解决。提出的 3RGS基于大规模重建先验知识MASt3R-SfM，能够联合优化3DGS和相机参数。联合优化的两大挑战：对SfM初始化质量的敏感性，以及全局优化能力有限导致的次优重建结果。我们的3R-GS通过整合优化策略克服了这些问题，即使在相机配准不精确的情况下也能实现稳健的场景重建。大量实验表明，3R-GS在保持计算效率的同时，实现了高质量视图合成与精准相机位姿估计的完美平衡。

二、相关工作：CF-3DGS（COLMAP-Free 3DGS）

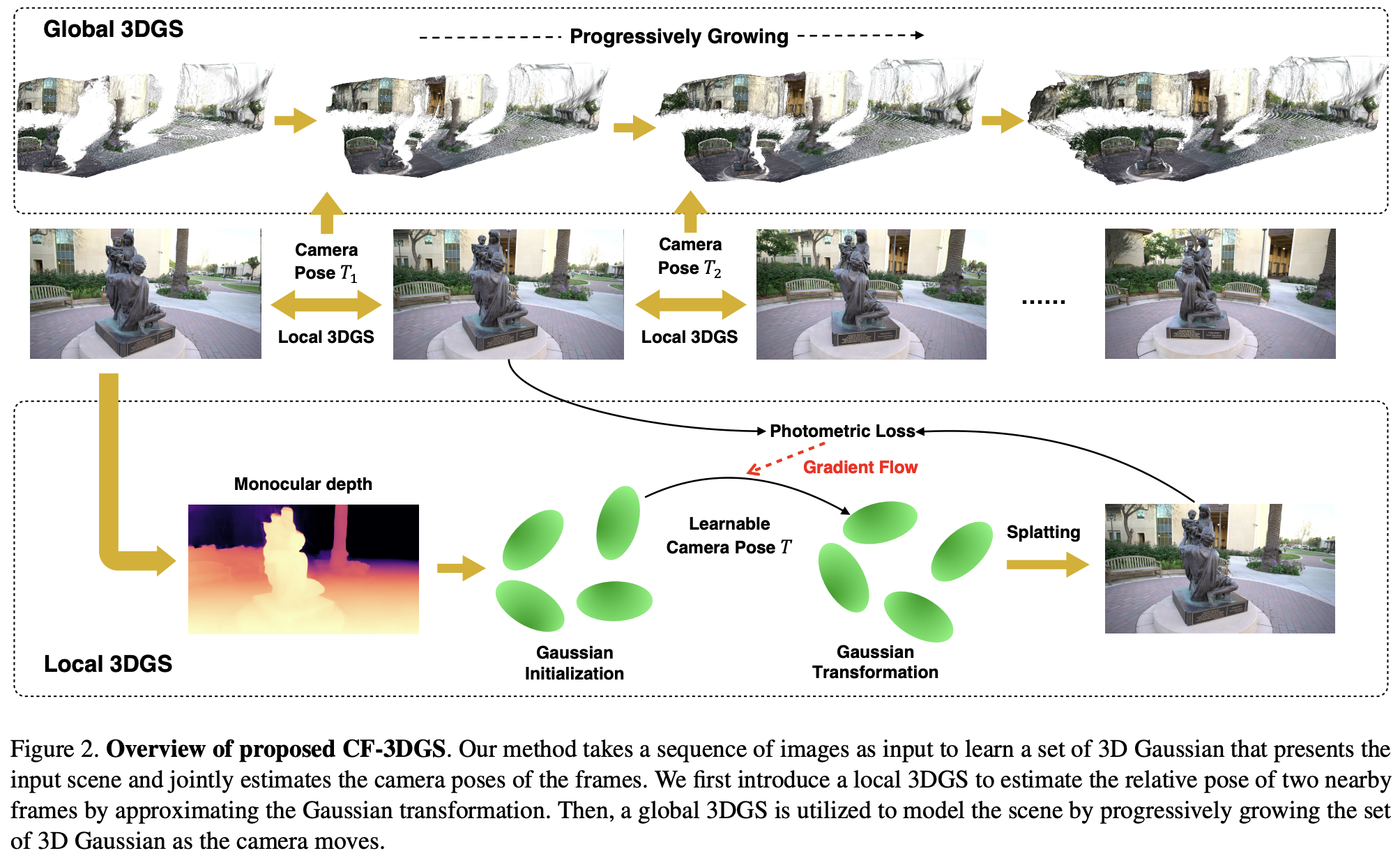
在这里插入图片描述

核心思想：

1.显式点云表达（3D-GS特色）
2.视频帧的时间连续性（用于近邻帧相对位姿估计）
3.从局部到全局的高斯集合构建方式

2.1 Local 3DGS：估计相对相机位姿

步骤一：初始化局部高斯点集

用单目深度网络（如DPT）从当前帧 $I_t$ 获取深度图 $D_t$ ，将其点云初始化 $G_t$ 。目标是最小化渲染图与当前帧的重建误差：

在这里插入图片描述
步骤二：优化相对位姿

利用已训练好的3D-GS $G_t^∗$ ，冻结其所有属性，仅学习一个刚体变换 $T_t$ ，使其变换后能拟合帧 $t + 1$ ：

在这里插入图片描述
由于帧间距离小，变换小、易优化；优化变量仅为旋转（四元数）+ 平移（3D 向量）。优点：

利用近邻帧的局部几何对齐来估计相对相机姿态；
避免了全局图优化所带来的高维非凸问题；
更快收敛，适合大规模视频。

2.2 Global 3DGS：逐帧更新构建全局模型

局部对齐只能估计相邻帧之间的相对变换，但构建完整场景需要一个不断增长的全局点云模型。

维护一个全局 $G_{global}$ ；每接收到一帧，就通过累计 $T$ 变换推导出与第一帧的相对位姿；将当前帧的局部高斯投影进全局模型，并联合优化。

三、主要方法

现有的3DGS高度依赖于准确的相机pose——通常以传统结构从运动技术（如COLMAP [5])获取的姿态作为输入，但在无纹理的室内环境等场景中往往表现不佳。为此，我们基于结合了大型重建先验[即MASt3R-SfM]的，来稳健地估计相机位姿。

虽然MASt3R-SfM在不同条件下的鲁棒性优于COLMAP [38]等传统SfM方法，但由于缺乏像素级精度，其估计的相机位姿仍存在不足。简单优化相机位姿，只能获得有限改进，引发——对初始化的敏感性和位姿优化效率低下。为应对这些挑战，我们提出以下创新方案：

(1)基于马尔可夫链蒙特卡洛方法的鲁棒姿态优化策略；
(2)采用多层感知机优化器的全局相机相关性模型；
(3)基于极线损失的无渲染几何约束方法。

在这里插入图片描述

3.1 基于 MCMC（马尔可夫蒙特卡洛）的位姿优化

动机：原始3DGS优化对初始点云极为敏感，如图3(a)所。若高斯基元初始化偏离理想位置，难以自我校正。这是因为光度渲染损失仅能提供局部区域内的梯度信息，使得基元难以突破局部最优解并达到正确位置。

此外，3DGS中的自适应 density 依赖于梯度的阈值。当引入新的训练目标时，需要手动调整或优化densification策略，这增加了优化过程的复杂性，还给相机位姿与3DGS联合优化带来了额外挑战。

在这里插入图片描述

解决方法：将3DGS重构为MCMC采样方法，显著提升了模型对初始条件的鲁棒性。该方法将训练过程视为从概率分布 $p (G)$ 中采样，该分布赋予3DGS以较高概率，使其能准确重建训练图像。研究发现，标准3DGS优化算法与随机梯度朗之万动力学（SGLD）更新机制具有相似特性：

在这里插入图片描述

其中 $η$ 是探索噪声， $a$ 和 $b$ 平衡了收敛和探索。通过这种噪声，可以在图3(a)中实现探索。此外，3DGS-MCMC通过principled state transitions（原则状态转移替）代传统的启发式致密化和剪枝方法，消除了对这些技术的依赖。我们还引入了其正则化项，以促进高斯分布的简约应用。

3DGS-MCMC实现了相机位姿与 3DGS 的鲁棒性联合优化，有效解决了“初始化敏感性”问题

3.2 基于MLP的全局位姿优化

动机：在实际应用中，多个相机常存在共同的漂移误差——虽然它们的相对位姿可能正确，但整体上会因共享的旋转和平移误差而偏离真实值（如图3©所示）。然而直接优化单个相机位姿时，将它们视为独立变量的做法，会导致原本正确的局部相对位姿失真，并因问题本身的非凸性特征，使优化过程更容易陷入局部极小值。

解决方案：我们引入了一个基于MLP的全局姿态优化器，该优化器能够从latent camera representation 中学习预测 pose corrections $T_i$

在这里插入图片描述
$z_i$ 是可学习的相机嵌入向量，与 MLP finer共同优化。校正包含平移（ $t_i∈R^3$ )和旋转（ $r_i∈R^6$ )两个分量。MLP采用零均值先验初始化，确保微调稳定。所有视图共享的MLP网络，能够捕捉全局位姿，从而实现更精准的相机调整。实际应用中，其效果显著优于直接优化单个相机姿态的方法。

3.3 无渲染的几何约束

MASt3R-SfM框架提供了精确的匹配对应关系，可为几何优化提供有效支持（MASt3R-SfM构建了一个稀疏场景图 $=(V,\xi)$ ，其中每个顶点 $I \in V$ 表示一张图像，每条边 $=(n,m)∈\xi$ 表示两张可能重叠的图像 $I^n$ 和 $I^m$ 之间的无向连接。基于该图结构，MASt3R-SfM计算出对应关系 $M^{n,m}$ 。）

在利用对应关系时，常用的优化方法包括3D-2D投影损失[12,41]和3D-3D损失[5,12]，二者均基于深度信息（如图3(b)所示）。3D-3D损失通过使用深度参数和相机参数将图像对中的对应点反投影到三维空间，计算其距离；而3D-2D投影损失则将这些三维点重新投影到图像平面，以计算与对应点的二维距离。这些方法通常需要多组图像对来模拟全局束调整，从而确保梯度更加一致。将两个损失整合到 3DGS 中面临重大挑战：3DGS渲染（包括RGB和深度）采用前序深度排序机制，且训练过程需要数万次迭代，其计算限制严重制约了每一步骤可处理的视图数量。若增加更多视图，不仅会大幅延长训练时间，还会导致内存消耗达到难以承受的程度。因此，在应用上述几何约束时，每一步只能考虑部分图像对，这使得真正全局的目标无法实现，最终导致次优结果。

解决方案：我们提出了一种 基于极线距离的无渲染全局几何约束方法 。通过MASt3R-SfM提供的图像对应关系 $M^{n,m}$ ，定义了如下损失：

在这里插入图片描述

$conf_i$ 表示MASt3R提供的点对 $(x, x^{'})$ 的置信度， $d (x, x^{'})$ 则是 (基于相机位姿和内参计算出的) 基础矩阵 $F$ 对应的对称外极距离。与PoRF [2]不同，我们在每次训练迭代中都会考虑所有图像对 $(n,m)∈\xi$ 的对应关系，这使得相机位姿的优化过程更具全局性信息。虽然MASt3R-SfM能为每对图像提供数千个对应关系，但实验表明实际只需数百个即可满足需求，因此我们采用均匀子采样策略处理这些对应关系。

总体训练目标

总体训练目标将原始3DGS渲染损失与3DGS-MCMC [24]中的额外正则化项相结合，并结合上述公式中的几何约束 $L_{geo}$ 。

在这里插入图片描述

$eig_j()$ 表示协方差矩阵的第 $j$ 个特征值。

实验

数据集：Tanks and Temples[25]、MipNeRF360 [1]和DTU [18]，分别选取四个代表性场景进行测试。Mip-NeRF360数据集包含室内和室外场景，这些场景通过沿360度轨迹均匀分布的摄像头拍摄，每个场景约含100-300张图像。《Tanks and Temples》在相机位姿和场景比例方面与前者类似，但在光照效果和外观表现上差异更大。相比之下，DTU专注于受控光照下的物体级室内场景，每个序列包含49或64张图像，并配有精确的真实位姿数据。

评估指标。参照BARF [27]和CF-3DGS [15]，对Novel View Synthesis（NVS）及相机位姿配准技术进行评估，测试训练视图下平均旋转误差与绝对轨迹误差（ATE）的均方根误差（RMSE）[31]（米）。在相机位姿评估中，我们报告了。为消除相似变换的影响，我们采用Procrustes分析法对优化后的训练位姿与真实值进行相机位置校准，该方法参考了先前研究[27]。针对NVS技术，我们报告了PSNR、SSIM [46]和LPIPS [59]指标

实现细节。我们的方法基于gsplat [53]在PyTorch上实现。实验统一权重： $λ_{D-SSIM}$ = 0.2， $λ_o = 0.01$ ， $λ_Σ = 0.01$ ， $λ_{geo}= 2$ 。我们发现极线几何约束 $λ_{geo}$ 在3DGS的早期训练阶段起着关键作用，有助于建立正确的几何结构，但其影响在后期阶段逐渐减弱。因此我们将在3000次迭代后将 $λ_{geo}$ 值衰减至0。每次迭代都会采样并渲染单个训练视图。关键区别在于我们会在每个步骤中额外计算 $λ_{geo}$ ，并将相机位姿梯度通过位姿优化器及其关联的相机latent codes进行传播。所有实验均在配备24GB显存的NVIDIA RTX 4090显卡上完成。

1.完整视频序列的结果

对比方法。与四个前沿基准方法对本方法进行评估：3DGS [22]、Spann3R [43]、ZeroGS [7]和CF-3DGS [15]。为确保公平比较，3DGS使用MASt3R-SfM获取的相同相机位姿，并启用gsplat [53]优化相机位姿。由于Spann3R采用不同的场景表征方式，我们在3DGS训练中采用其预估的相机位姿并开启优化功能，保持与实验设置的一致性。ZeroGS未开源，直接引用论文结果。CF-3DGS的实验基于官方实现。

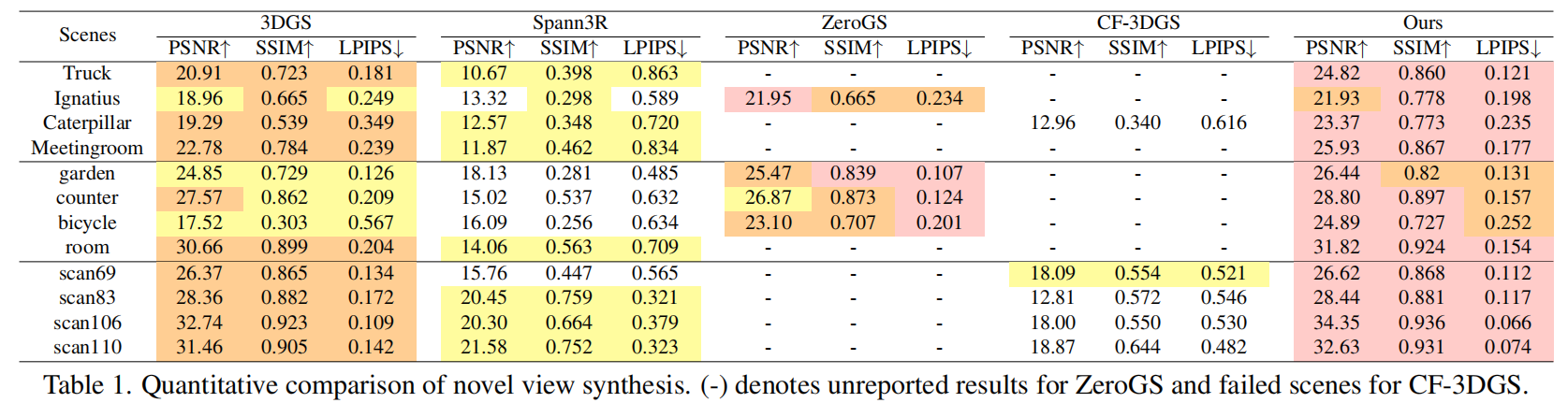
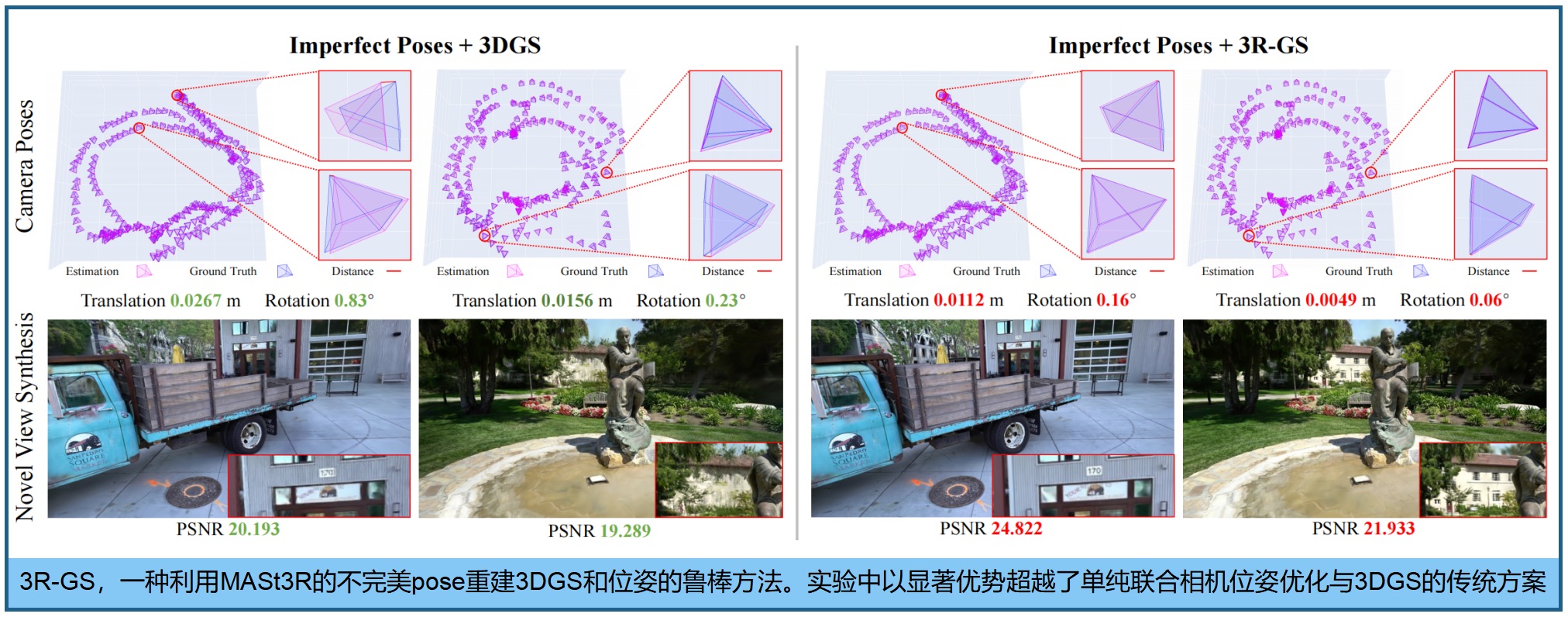
在这里插入图片描述

ZeroGS的表现略逊于本文，CF-3DGS在Mip-NeRF360和Tanks and Temples数据集上表现欠佳。这种失败主要归因于其渐进式训练流程中早期相机跟踪的损失问题，在摄像机运动较大的场景中尤为明显。

2.相机配准

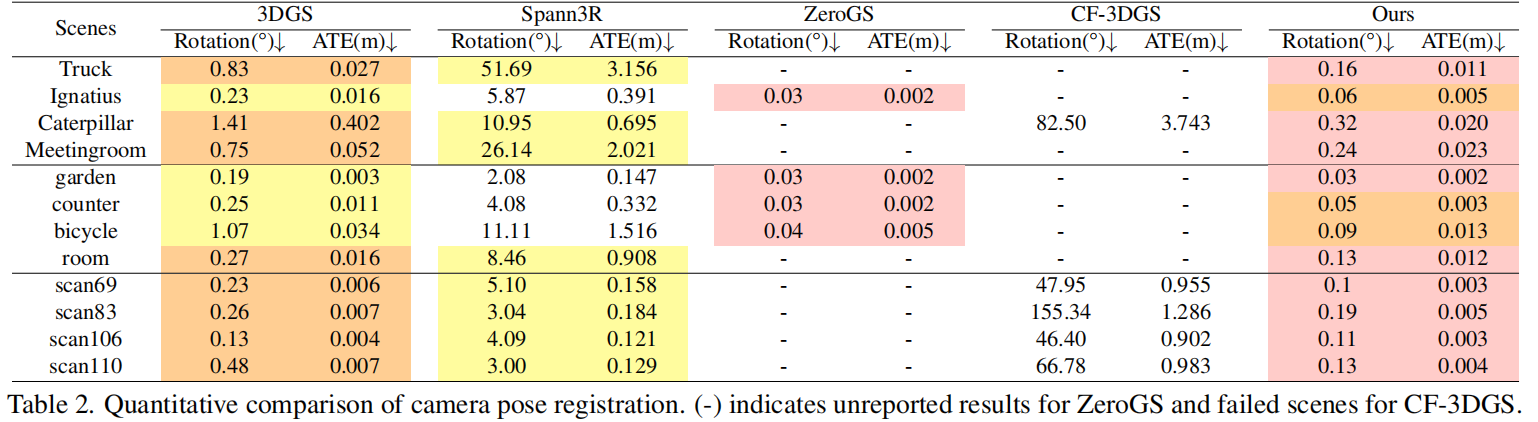
如表2和图5，方法显著优于（相机位姿优化的）3DGS，同时与ZeroGS的表现相当。两者在旋转误差上的微小差异（平均0.02°度）和平均ATE误差0.003米，几乎可以忽略不计——尤其是考虑到我们在新视角合成方面取得的卓越成果。此外，ZeroGS采用与传统增量式 SfM 相似的复杂两阶段训练策略，通过渐进式图像配准实现效果提升，而我们的方法仅需增强标准3DGS的SfM输出训练流程，就能获得具有竞争力的结果，且计算开销极小。

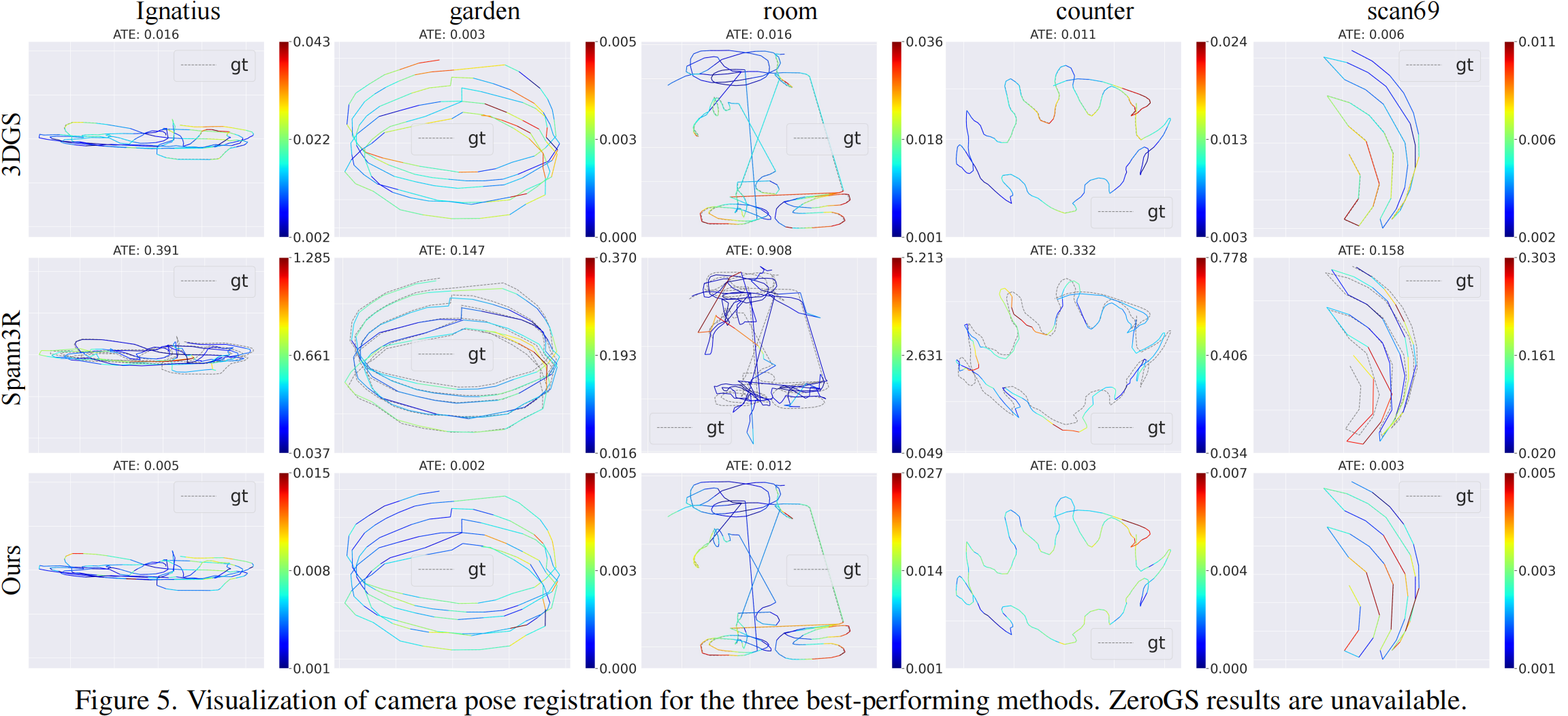
在这里插入图片描述

3. 短视频片段的评估结果

基于Tanks and Temples 数据集中的短视频片段对方法进行测试，实验流程参照CF-3DGS[15]方案并采用其预处理数据。如表3和表4。为确保公平比较，我们将绝对轨迹误差（ATE）按100倍比例缩放，并通过平移和旋转两种方式实现相机位姿与真实值的对齐。所有定量结果均采用文献[Colmap-free 3d gaussian splatting]提供的官方评估代码。

在这里插入图片描述