具有良好非周期相关特性的多相码（Polyphase Codes，亦称 Frank Codes）——论文阅读

Frank 于1963年提出的多相码（Frank码）通过N×N相位矩阵构造，在非周期自相关中展现出单一主峰和极低旁瓣特性。当相位数N>5时，其主旁瓣比显著优于最优二元码。该码采用逐行读取的相位序列生成方式，具有周期性零点、单位旁瓣等结构化特性。研究表明，随着码长增加，多相码的性能优势更为明显，为高时宽带宽积系统提供了有效解决方案。论文还分析了多普勒效应的影响，并讨论了工程实现要点。Frank

DuHz

1076人浏览 · 2025-10-07 14:32:14

DuHz · 2025-10-07 14:32:14 发布

具有良好非周期相关特性的多相码（Polyphase Codes，亦称 Frank Codes）

R. Frank, “Polyphase codes with good nonperiodic correlation properties,” in IEEE Transactions on Information Theory, vol. 9, no. 1, pp. 43-45, January 1963, doi: 10.1109/TIT.1963.1057798.

这篇由 Robert L. Frank 于 1963 年发表于《IEEE Transactions on Information Theory》的论文，开创性地提出了一类 N 相脉冲序列码（常称 Frank 码）。该类码在非周期自相关（aperiodic ACF）中呈现出单一尖锐主峰与极低旁瓣，对雷达与通信系统中的脉冲压缩尤为关键。作者通过计算与分析指出：当相位数 $N > 5$ 时，这些多相码的主旁瓣比显著优于当时通过穷举搜索得到的最优二元码（仅含 ${0∘,180∘}\{0^\circ,180^\circ\}$ 两相）。

引言

在雷达与通信系统中，为了在有限峰值功率下发射高能量信号以提升探测距离与抗干扰能力，同时保持极高的时间（距离）分辨率，脉冲压缩技术应运而生。其核心做法是：发射时间上较宽、内部相位/频率被调制的脉冲；在接收端以匹配滤波把能量“压缩”到时间上极窄的脉冲。理想输出的自相关只应有一个极高的主峰，其他时移处（旁瓣）应尽可能低。

彼时对二元码的研究已很深入，但除长度 $≤13\le 13$ 的 Barker 码外，较长序列几乎难以兼具良好非周期相关特性，这限制了高压缩比（长序列）场景的应用。为突破此瓶颈，Frank 提出了相位数 $N > 2$ 的多相码并给出简洁的工程实现思路。

编码的生成方法

Frank 码基于一个 $N×NN\times N$ 的整数矩阵构造，其元素为基本相位角的整数倍系数。设基本相位角

$\phi=\frac{2\pi p}{N},$

其中 $N$ 为相位数， $p$ 与 $N$ 互质（文中多取 $p = 1$ ）。矩阵第 $i$ 行、第 $j$ 列元素为

$a_{i,j}=(i\cdot j)\bmod N,\qquad i,j\in\{0,1,\dots,N-1\}.$

对应的复指数码元为

$s_{i,j}=e^{\,\mathrm{j}\,a_{i,j}\phi}=e^{\,\mathrm{j}\,\tfrac{2\pi}{N}(i j)}.$

将矩阵按逐行（从左到右、由上到下）读出并串接，即得长度 $L=N^2$ 的序列：

$\underbrace{s_{0,0},\dots,s_{0,N-1}}_{\text{第 0 行}};\; \underbrace{s_{1,0},\dots,s_{1,N-1}}_{\text{第 1 行}};\;\dots;\; \underbrace{s_{N-1,0},\dots,s_{N-1,N-1}}_{\text{第 }N-1\text{ 行}}.$

直觉动机：优秀二元码与线性调频（LFM）信号往往呈现“从慢变到快变”的瞬时频率/相位变化。矩阵首行相位不变（全 0），随后各行的相位步进逐行增大，故从左上角开始的逐行读出与上述直觉一致，且数值验证效果最佳。

非周期自相关特性

设序列长度 $L=N^2$ ，非周期自相关定义为

$R(m)=\sum_{k=0}^{L-1-m}s_k^{*}\,s_{k+m},\qquad m=0,1,\dots,L-1.$

主峰与能量
主峰 $R(0)=∑k∣sk∣2=LR(0)=\sum_k|s_k|^2=L$ （码元等幅为 1）。

旁瓣规律（核心发现与猜想）
对 $N≤8N\le 8$ 的逐点计算显示：最大旁瓣幅度 $R(m)|_{\max}$ 等于若干单位矢量以等角间隔 $2π/N2\pi/N$ 相加的矢量和模值：

$N$ 偶数：等于 $N /2$ 个单位矢量的矢量和；
$N$ 奇数：等于 $(N + 1) /2$ 个单位矢量的矢量和。
该结论在论文中作为强有力的下界猜想提出（当时尚无普适证明），并与数值吻合良好。

结构化性质

周期性零点：当时移为 $m = k N$ （ $k$ 为正整数）时， $R (m) = 0$ 。缘由是矩阵各行彼此正交。
单位旁瓣：当 $m=kN±1m=kN\pm1$ 时， $∣ R (m) ∣ = 1$ 。
共轭对称： $∣ R (m) ∣ = ∣ R (L - m) ∣$ 。
旁瓣包络对称：已计算的多个 $N$ 值案例均表现出左右对称的旁瓣包络与清晰的层次结构。

下图示意（为突出旁瓣形态，主峰未按比例绘制，旁瓣取绝对值）

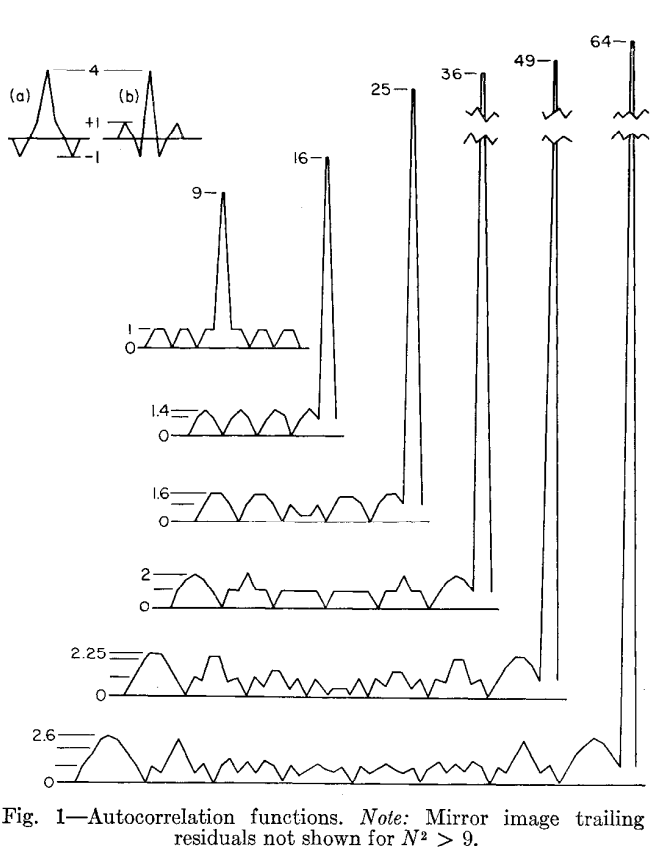
图 1：自相关函数示意（ $N=2∼8N=2\sim8$ ）

性能比较

论文将 Frank 多相码与当时最优二元码的主峰/最大旁瓣比（PSL）做对比，横轴为码长（对数），纵轴为主峰与最大旁瓣幅度比。

图 2：编码性能比较（实线为计算验证，虚线为基于猜想的推断）

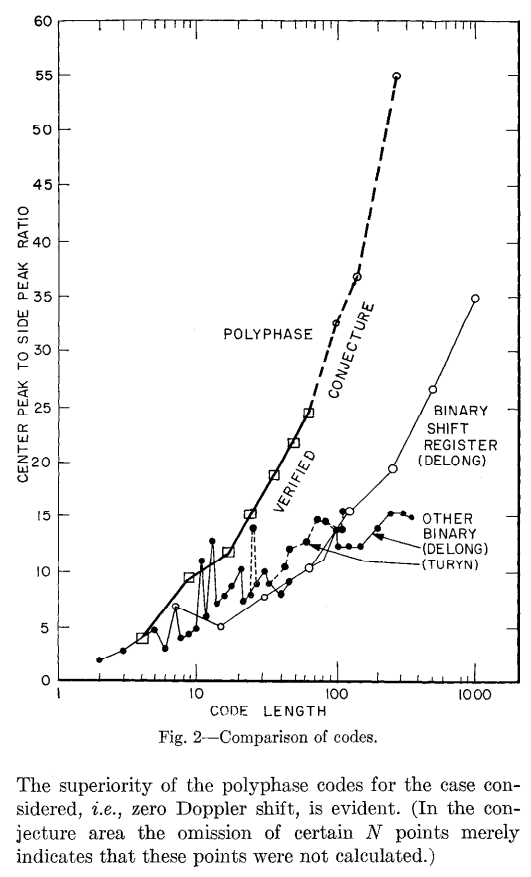
结论明确：在零多普勒理想条件下，多相码的 PSL 随码长快速提升，整体显著优于二元码，且码长越大优势越明显，为高时宽带宽积的雷达系统提供了优选波形。

多普勒效应的影响

论文对多普勒频移给出了直观分析：长度为 $N^2$ 的 Frank 码在频移下的相关行为与 LFM 的“模糊函数”非常相似——频率偏移在相关输出上近似对应时间平移。

以 $N = 4$ （码长 16）为例，若受到 $f_d=N/T=4/T$ 的频偏（ $T$ 为序列总时长），等效于对每个码元叠加一条线性相位斜率。变换后的序列等价于用矩阵的另一行作为起点重新读出的序列：
0, 1, 2, 3; 0, 2, 0, 2; 0, 3, 2, 1; 0, 0, 0, 0
与原匹配滤波器相关时，主峰不会展宽或失配，而是以幅度约为原主峰的 $3/4$ 在新的时移点（偏移 4 个码元）处出现。这种时频耦合特征与 LFM 十分一致。

实现与工程要点

结构规律性：长度 $N^2$ 的序列由 $N$ 个长度 $N$ 的组构成。组内相位以恒定步长均匀递增，组与组之间的步长再以固定增量变化。
匹配滤波器：可用 $N^2$ 抽头的延迟线实现，对第 $k$ 抽头施加与原序列时间反转共轭对应的相移。可将相同相移的抽头先合并，通过公共移相器处理后再求和，降低硬件复杂度。
量化与容差（实用补充）：实现中相位量化、幅度误差、定时抖动与平台杂散会导致旁瓣抬升。通常选择较大的 $N$ 有助于 PSL，但需平衡 DAC/移相器分辨率 与 系统带宽。

术语与符号小结

$N$ ：相位数（例如 $N = 4$ 即 4 相码）
码长 $L=N^2$
基本相位角 $ϕ=2π/N\phi=2\pi/N$ （本文取 $p = 1$ ）
元素/码元： $2π(ij)/Ns_{i,j}=e^{\,\mathrm{j}\,2\pi (i j)/N}$
非周期自相关： $R(m)=∑k=0L−1−msk∗sk+mR(m)=\sum_{k=0}^{L-1-m}s_k^{*} s_{k+m}$
主旁瓣比（幅度）： $PSL=∣R(0)∣/max⁡m≠0∣R(m)∣\text{PSL}=|R(0)|/\max_{m\ne 0}|R(m)|$ ，以 dB 计为 $20log⁡10PSL20\log_{10}\text{PSL}$

附录：数学概念示例

1）码的生成

构造 $4×44\times 4$ 矩阵 $4a_{i,j}=(i j)\bmod 4$ ：

$\begin{aligned} i=0:&\ (0,0,0,0)\\ i=1:&\ (0,1,2,3)\\ i=2:&\ (0,2,0,2)\\ i=3:&\ (0,3,2,1) \end{aligned}$

逐行串接即得长度 16 的序列：

0, 0, 0, 0; 0, 1, 2, 3; 0, 2, 0, 2; 0, 3, 2, 1

其中数字 $k$ 表示相位 $k⋅(2π/4)=k⋅(π/2)k\cdot (2\pi/4)=k\cdot (\pi/2)$ 。

2）非周期自相关（ACF）

$R(m)=\sum_{k=0}^{15-m} s_k^{*} s_{k+m},\quad R(0)=16.$

举二元对照小例： $+ 1, + 1, - 1, + 1$ 在 $m = 1$ 时
$R(1)=1⋅1+1⋅(−1)+(−1)⋅1=−1R(1)=1\cdot 1+1\cdot (-1)+(-1)\cdot 1= -1$ 。
多相情形完全类比，只是 $s_k$ 位于复平面单位圆上。

3）最大旁瓣幅度（ $N = 4$ ）

猜想给出最大旁瓣为 $N /2 = 2$ 个单位矢量、相邻夹角 $2π/N=π/22\pi/N=\pi/2$ 的矢量和：

$\mathrm{j}0)+(0+\mathrm{j}1)=1+\mathrm{j},\quad |S|=\sqrt{2}\approx 1.414,$

与数值图示中最大旁瓣 $≈1.4\approx 1.4$ 一致。

4）PSL 计算

$P_{\text{main}}=16,\quad P_{\text{side}}=\sqrt{2},\quad \text{PSL}=\frac{16}{\sqrt{2}}\approx 11.3,\quad \text{PSL}_{\text{dB}}=20\log_{10}(11.3)\approx 21.1\ \text{dB}.$

与相关码型的简要关系（扩展）

Barker 码：二元、长度有限（ $≤13\le 13$ ）具优异 ACF 的经典序列；长码稀缺。
Frank 码：本文主角，基于 $Na_{i,j}=(ij)\bmod N$ 的 $N$ 相构造，擅长非周期相关性能。
其它多相/CAZAC 类：后续研究中出现了对周期相关更强的常幅零自相关（CAZAC）序列与 P1–P4 等多相脉压码型；应用选择应结合非周期/周期指标与系统多普勒环境综合权衡。