基于多普勒频率和距离变化率联合测量的增强型速度估计方法

Lim S, Jung J, Kim J, et al. Enhanced velocity estimation based on joint Doppler frequency and range rate measurements[C]//2022 Thirteenth International Conference on Ubiquitous and Future Networks (ICUFN). IEEE, 2022: 217-221.

1. 引言

现代汽车雷达系统在高级驾驶辅助系统（ADAS）和自动驾驶中扮演着不可或缺的角色。与激光雷达和摄像头等其他传感器相比，雷达的独特优势在于其能够直接测量目标的速度信息。这种速度测量能力基于多普勒效应，通过发射无线电信号并测量其多普勒频率来实现。然而，奈奎斯特采样定理对可检测的最大多普勒频率施加了基本限制，导致超过奈奎斯特速率的速度会产生混叠现象。在MIMO雷达系统中，为了实现多路复用，通常采用时分复用技术，通过划分时隙来交替进行传输。这种方式增加了同质啁啾脉冲之间的时间间隔，导致无模糊检测区域进一步缩小。由于速度估计是雷达的基本功能，解决速度模糊问题对于实现可靠的自动驾驶至关重要。

现有的研究已经提出了多种方法来解决这一挑战。一些研究通过修改发射信号波形来解决速度模糊，例如在相邻啁啾之间添加频移，或使用具有不同重复间隔的信号并应用中国剩余定理来扩展最大可检测速度。然而，这些方法的主要缺点是需要修改现有硬件。另一种方法利用雷达系统的距离估计结果，通过相邻帧之间的距离变化获得粗略的速度估计，或使用卡尔曼滤波器跟踪目标运动来解决速度模糊。但这些方法基于两个相邻帧之间的距离变化，当距离变化不够大而无法被雷达检测时，性能会显著下降。

本文提出了一种增强型速度消歧方法，克服了上述方法的局限性。该方法的核心创新在于结合基于多普勒频率的速度估计和基于距离变化率的速度估计。前者虽然存在模糊性但精度很高，后者虽然精度较低但不存在模糊性。通过巧妙地结合这两种估计的优势，可以得到既准确又无模糊的速度估计结果。

2. FMCW雷达系统中的速度估计

2.1 FMCW雷达系统的工作原理

频率调制连续波（FMCW）雷达系统采用线性频率调制方案，其中信号的相位是时间的二次函数。发射的啁啾信号可以用数学表达式描述为：

$$s(t)=\cos \left[2\pi \left(f_{c}t+\frac{K}{2}{t}^2\right)\right],0\le t\le T_c$$

其中，$f_c$表示载波频率（通常在汽车雷达中为77 GHz），$K$是频率斜率（也称为调频斜率），$T_c$是单个啁啾信号的持续时间。

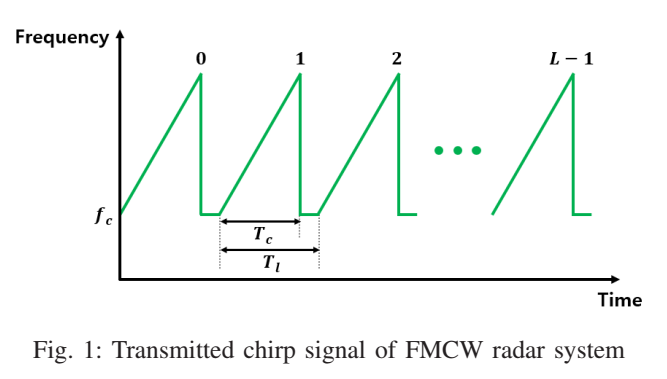
图1描述：图1展示了FMCW雷达系统的发射啁啾信号示意图。横轴表示时间，纵轴表示频率。可以看到频率随时间线性增加，形成锯齿波形状。在一个完整的帧周期$T_f$内，连续发射$L$个啁啾脉冲（图中显示为0到$L-1$），每个啁啾之间的间隔为$T_l$。这种重复的线性调频信号构成了FMCW雷达的基本发射波形。

发射信号遇到雷达探测范围内的散射体后被反射，延迟的回波信号被接收天线接收。接收信号与发射信号混频，经过低通滤波去除高频分量，然后使用正交解调技术。采样后的接收信号可以用复指数形式表示为：

x[m,l]≃exp⁡{j2π(fbmTs+fdlTl+ϕ)}x[m, l] \simeq \exp\{j2\pi(f_b m T_s + f_d l T_l + \phi)\}x[m,l]≃exp{j2π(fb​mTs​+fd​lTl​+ϕ)}

其中：

• $m=0,1,\cdots ,M-1$表示快时间维度的采样索引
• $l=0,1,\cdots ,L-1$表示慢时间维度的啁啾索引
• $T_s$是快时间采样周期
• $T_l$是啁啾重复间隔
• $\varphi$是剩余相位项
• $f_b$是差拍频率（沿$m$轴）
• $f_d$是多普勒频率（沿$l$轴）

这个信号通常被称为差拍信号，包含了目标的距离和速度信息。差拍频率和多普勒频率与目标的物理参数之间存在以下关系：

$$f_b=\frac{2KR}{c},f_d=\frac{2v}{\lambda }$$

其中$R$是目标距离，$v$是目标径向速度，$c$是光速，$\lambda =c/f_c$是信号波长。

通过对差拍信号$x[m,l]$应用二维快速傅里叶变换（2D FFT），可以同时估计这两个频率。具体而言，首先沿快时间维度（$m$轴）进行FFT得到距离信息，然后沿慢时间维度（$l$轴）进行FFT得到速度信息。因此，目标的距离和速度可以分别估计为：

$$\hat{R}=\frac{c}{2K}{\hat{f}}_b,\hat{v}=\frac{\lambda }{2}{\hat{f}}_d$$

2.2 速度模糊现象的数学分析

速度估计的核心在于准确测量目标的多普勒频率。然而，根据奈奎斯特采样定理，采样频率决定了可以无模糊恢复的最大频率。在慢时间维度上，采样频率等于$1/T_l$，因此可检测的多普勒频率必须满足：

$$|f_d|\le \frac{1}{2T_l}$$

将这个频率限制转换为速度限制：

$$|v|\le \frac{\lambda }{4T_l}\triangleq v_{max}$$

这里定义$v_{max}=\lambda /(4T_l)$为最大无模糊速度，速度的无模糊检测区域为$[-v_{max},v_{max}]$。

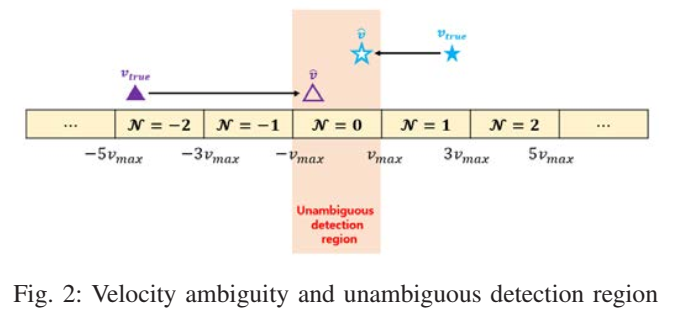
图2描述：图2形象地展示了速度模糊现象和无模糊检测区域。图中央的橙色区域表示无模糊检测区域$[-v_{max},v_{max}]$。当真实速度$v_{true}$（用蓝色星号标记）超出这个区域时，由于相位的$2\pi$周期性，它会被错误地映射到无模糊区域内的某个位置$\hat{v}$（用红色圆圈标记）。图中展示了不同的模糊区域，用$N=-2,-1,0,1,2,\dots$标记，每个区域的宽度为$2v_{max}$。

由于复指数函数的$2\pi$周期性，超出无模糊检测区域的速度会折回到该区域内。数学上，估计速度与真实速度之间的关系可以表示为：

$$\hat{v}=v_{true}-\lfloor \frac{v_{true}+v_{max}}{2v_{max}}\rfloor \times 2v_{max}$$

定义模糊参数$N$为：

$$N=\lfloor \frac{v_{true}+v_{max}}{2v_{max}}\rfloor$$

则有：

$$\hat{v}=v_{true}-N\times 2v_{max}$$

这个整数$N$决定了真实速度所在的模糊区域。如果能够确定$N$的值，就可以通过以下公式恢复真实速度：

$$v_{true}=\hat{v}+N\times 2v_{max}$$

3. 提出的速度消歧方法

3.1 方法框架概述

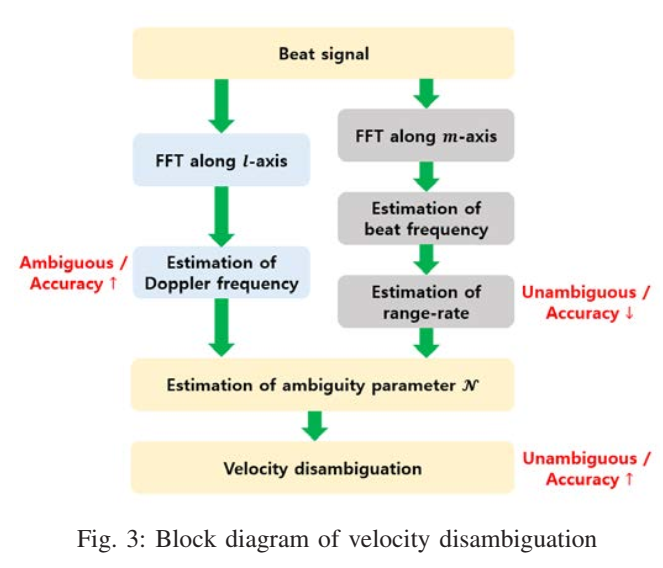
图3描述：图3展示了提出的速度消歧方法的完整框架。系统输入是差拍信号，经过两条并行的处理路径。左侧路径（标记为"Ambiguous/Accuracy↑"）通过FFT沿$l$轴提取多普勒频率，得到高精度但存在模糊的速度估计$\hat{v}$。右侧路径（标记为"Unambiguous/Accuracy↓"）通过FFT沿$m$轴提取多帧的距离信息，然后估计距离变化率，得到无模糊但精度较低的速度估计$\dot{v}$。最后，这两个估计值被送入模糊参数估计模块，确定$N$值并实现速度消歧，输出无模糊且高精度的速度估计。

提出的速度消歧方法包含三个主要阶段，每个阶段都有其特定的功能和数学处理过程。

3.2 第一阶段：基于多普勒频率的模糊速度估计

在第一阶段，通过传统的多普勒处理获得高精度的速度估计。具体步骤如下：

1. 对差拍信号$x[m,l]$沿慢时间维度（$l$轴）应用FFT：
   $$X[m,k]=\sum _{l=0}^{L-1}x[m,l]\exp \left(-j2\pi \frac{kl}{L}\right)$$

2. 对每个距离单元$m$，寻找峰值对应的频率索引$k_{peak}$

3. 估计多普勒频率：
   $${\hat{f}}_d=\frac{k_{peak}}{L\cdot T_l}$$

4. 计算模糊速度估计：
   $$\hat{v}=\frac{\lambda }{2}{\hat{f}}_d$$

这个估计值始终位于$[-v_{max},v_{max}]$区间内，具有高精度但存在模糊性。

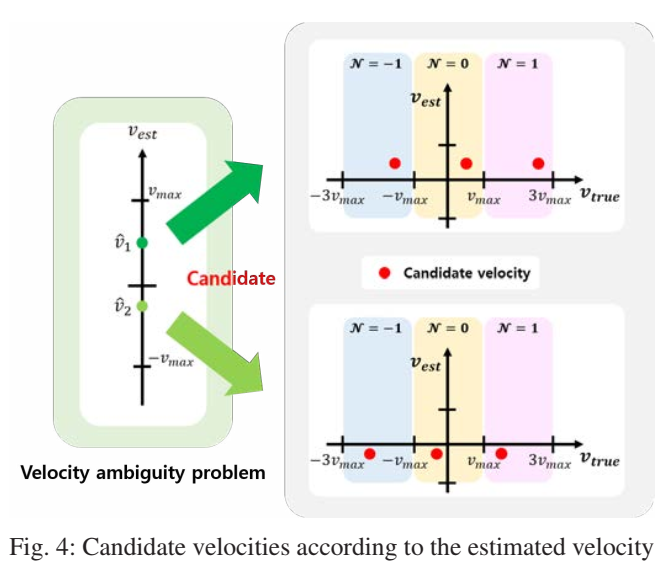
图4描述：图4说明了根据估计速度确定候选速度的过程。中心显示了估计得到的模糊速度$\hat{v}$。根据不同的模糊参数$N$值（$N=-1,0,1$等），存在多个候选真实速度，它们分布在不同的模糊区域中。每个候选速度与估计速度的关系为$v_{candidate}=\hat{v}+N\times 2v_{max}$。图中用不同颜色的区域表示不同的模糊区间，红色点表示各个候选速度的位置。

3.3 第二阶段：基于距离变化率的无模糊速度估计

第二阶段通过测量多帧的距离变化来获得无模糊但精度较低的速度估计。这个过程利用了目标运动的连续性：

1. 对$N_f$个连续帧，分别估计目标距离：

   • 对第$k$帧的差拍信号沿快时间维度（$m$轴）应用FFT
   • 提取峰值对应的差拍频率${\hat{f}}_{b,k}$
   • 计算距离估计：${\hat{R}}_k=\frac{c}{2K}{\hat{f}}_{b,k}$

2. 建立距离-时间的线性模型：
   $${\hat{R}}_k=T_f\dot{v}k+C+{ϵ}_k$$

   其中${ϵ}_k$是测量噪声。

3. 构造线性方程组的矩阵形式：
   $$\left[\begin{array}{cc}0& 1\\ T_f& 1\\ 2T_f& 1\\ ⋮& ⋮\\ (N_f-1)T_f& 1\end{array}\right]\left[\begin{array}{c}\dot{v}\\ C\end{array}\right]=\left[\begin{array}{c}{\hat{R}}_0\\ {\hat{R}}_1\\ {\hat{R}}_2\\ ⋮\\ {\hat{R}}_{N_f-1}\end{array}\right]$$

4. 应用最小二乘法求解，提取$\dot{v}$作为速度估计

3.4 第三阶段：模糊参数确定与速度重建

最后阶段结合两个速度估计来确定模糊参数$N$：

1. 定义优化问题：
   $$\hat{N}=\arg \underset{N}{\min }|\hat{v}+N\times 2v_{max}-\dot{v}|$$

2. 考虑到$N$必须是整数，闭式解为：
   $$\hat{N}=\lfloor \frac{\dot{v}-\hat{v}}{2v_{max}}+0.5\rfloor$$

3. 重建无模糊速度：
   $$v_{final}=\hat{v}+\hat{N}\times 2v_{max}$$

4. 性能评估与仿真结果

4.1 仿真参数设置

为了验证提出方法的有效性，使用了表1所示的FMCW雷达系统参数进行仿真。这些参数代表了典型的77 GHz汽车雷达配置。

表1：FMCW雷达系统参数

雷达参数	数值
载波频率 $f_c$	77 GHz
频率斜率 $K$	10 MHz/μs
采样周期 $T_s$	0.1 μs
啁啾间隔 $T_l$	50 μs
每啁啾采样数 $M$	256
每帧啁啾数 $L$	128
帧持续时间 $T_f$	10 ms

基于这些参数，计算得到最大无模糊速度为：
$$v_{max}=\frac{\lambda }{4T_l}=\frac{c/f_c}{4\times 50\times 10^{-6}}=9.73\text{ m/s}$$

4.2 多目标场景测试

设置了三个具有不同速度特征的目标来全面测试算法性能：

表2：目标的距离和速度参数

目标	距离	真实速度	模糊参数$N$	预期估计速度
A	30 m	15 m/s	1	-4.46 m/s
B	50 m	5 m/s	0	5 m/s
C	20 m	-22 m/s	-2	-2.54 m/s

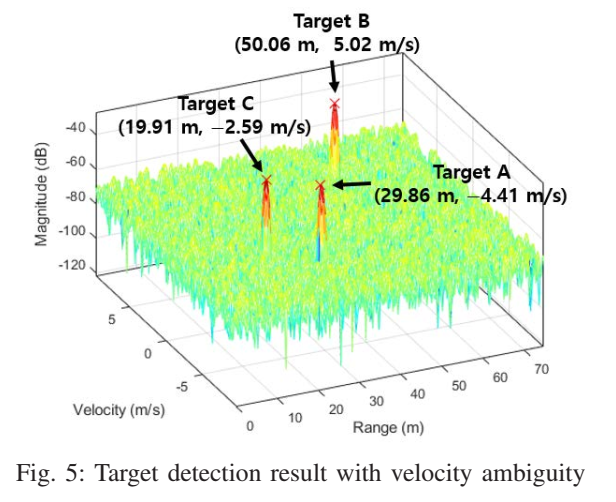
图5描述：图5展示了应用2D FFT后的雷达频谱图，呈现了存在速度模糊时的目标检测结果。图中横轴表示距离（0-70 m），纵轴表示速度（-120到5 m/s的模糊区间）。三个目标在频谱中表现为明亮的峰值点。目标B（位于50.06 m, 5.02 m/s）被正确检测，因为其速度在无模糊区间内。而目标A（位于29.86 m，错误地显示为-4.41 m/s）和目标C（位于19.91 m，错误地显示为-2.59 m/s）由于速度模糊而被错误估计。颜色条表示信号强度，从深蓝色（低）到黄色（高）。

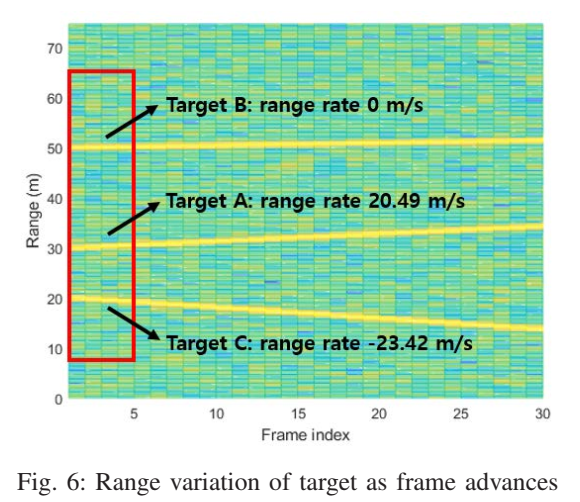
图6描述：图6展示了三个目标的距离随帧索引变化的情况。横轴是帧索引（0-30），纵轴是距离（10-70 m）。图中可以清晰看到三条具有不同斜率的轨迹：目标A的轨迹（斜率为正，约20.49 m/s）表明目标远离雷达；目标B的轨迹（几乎水平，0 m/s）表明目标静止；目标C的轨迹（斜率为负，约-23.42 m/s）表明目标接近雷达。这些斜率提供了无模糊但精度较低的速度估计。

4.3 算法性能对比

通过计算，三个目标的模糊参数$N$被正确估计为1、0和-2，最终重建的无模糊速度分别为15.06 m/s、5.02 m/s和-22.05 m/s，与真实值高度吻合。

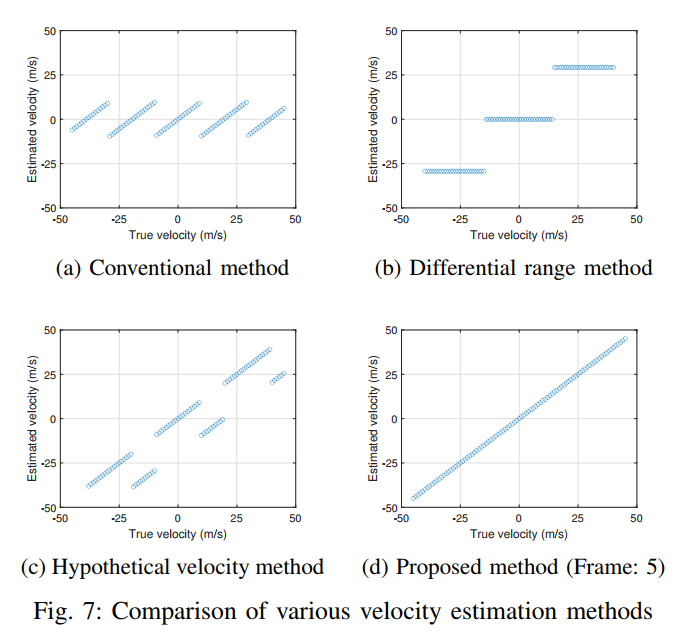
图7描述：图7通过四个子图对比了不同速度估计方法的性能。每个子图中，横轴表示真实速度（-50到50 m/s），纵轴表示估计速度（-50到50 m/s）。理想情况下，所有点应落在45度对角线上。

• (a) 传统方法：显示了严重的速度折叠现象，超出$\pm v_{max}$的速度被错误地映射
• (b) 差分距离方法：估计值分散，精度很低
• © 假设速度方法：大部分区域表现良好，但存在不连续跳变
• (d) 提出的方法（5帧）：所有点都准确落在对角线上，成功解决了速度模糊

4.4 帧数选择的影响分析

研究了用于距离变化率估计的帧数$N_f$对性能的影响。当帧数较少时（如2-3帧），距离变化率估计的方差较大，可能导致模糊参数判断错误。随着帧数增加，估计精度提高，但计算延迟也相应增加。仿真结果表明，使用5帧（对应50 ms的数据累积）能够在精度和实时性之间达到良好平衡，对于所有测试场景都能正确确定模糊参数。

5. 结论

本文提出了一种创新的FMCW雷达速度消歧方法，通过智能地结合基于多普勒频率的高精度模糊速度估计和基于多帧距离变化率的低精度无模糊速度估计，成功解决了速度模糊问题。该方法的主要优势包括：

1. 普适性：无论雷达系统是否采用MIMO架构，方法都能有效工作
2. 兼容性：可直接应用于现有雷达硬件，无需修改信号波形
3. 实用性：仅需5帧数据（50 ms）即可实现可靠的速度消歧
4. 准确性：在整个速度范围内都能准确恢复真实速度

附录：数学推导

A. 差拍信号

考虑距离为$R(t)$、径向速度为$v$的运动目标。发射信号为：

$$s_{tx}(t)=A_{tx}\cos \left[2\pi \left(f_{c}t+\frac{K}{2}{t}^2\right)\right]$$

信号传播到目标并返回的总时延为：

$$\tau (t)=\frac{2R(t)}{c}=\frac{2(R_0+vt)}{c}$$

接收信号可以表示为：

$$s_{rx}(t)=A_{rx}\cos \left[2\pi \left(f_c(t-\tau )+\frac{K}{2}(t-\tau {)}^2\right)\right]$$

混频后的信号：

$$s_{IF}(t)=s_{tx}(t)\cdot s_{rx}(t)$$

应用三角恒等式$\cos A\cos B=\frac{1}{2}[\cos (A+B)+\cos (A-B)]$，并通过低通滤波去除和频分量，得到：

$$s_{IF}(t)=\frac{A_{IF}}{2}\cos \left[2\pi \left(f_c\tau -\frac{K}{2}{\tau }^2+Kt\tau \right)\right]$$

对于汽车雷达应用，$\tau \ll t$，可以忽略${\tau }^2$项：

$$s_{IF}(t)\approx \frac{A_{IF}}{2}\cos \left[2\pi \left(\frac{2f_c{R}_0}{c}+\frac{2f_{c}v}{c}t+\frac{2K{R}_0}{c}t+\frac{2Kv}{c}{t}^2\right)\right]$$

由于$v\ll c$，$\frac{2Kv}{c}{t}^2$项可以忽略，得到：

$$s_{IF}(t)\approx \frac{A_{IF}}{2}\cos \left[2\pi \left(\underset{f_b}{\underbrace{\frac{2K{R}_0}{c}}}t+\underset{f_d}{\underbrace{\frac{2f_{c}v}{c}}}t+{\varphi }_0\right)\right]$$

这就是差拍信号的最终形式，其中差拍频率$f_b$包含距离信息，多普勒频率$f_d$包含速度信息。

B. 速度模糊的频域分析

在离散时间域，第$l$个啁啾的采样信号为：

$$x[m,l]=A\exp \left[j2\pi \left(\frac{f_{b}m}{f_s}+\frac{f_{d}l}{f_{PRF}}+\varphi \right)\right]$$

其中$f_s=1/T_s$是快时间采样率，$f_{PRF}=1/T_l$是脉冲重复频率。

沿慢时间维度的离散傅里叶变换（DFT）为：

$$X[m,k]=\sum _{l=0}^{L-1}x[m,l]\exp \left(-j2\pi \frac{kl}{L}\right)$$

代入$x[m,l]$的表达式：

$$X[m,k]=A\exp (j\varphi )\exp \left(j2\pi \frac{f_{b}m}{f_s}\right)\sum _{l=0}^{L-1}\exp \left[j2\pi l\left(\frac{f_d}{f_{PRF}}-\frac{k}{L}\right)\right]$$

当$\frac{f_d}{f_{PRF}}=\frac{k}{L}$时，求和达到最大值$L$。但由于指数函数的周期性，当：

$$\frac{f_d}{f_{PRF}}=\frac{k+nL}{L},n\in \mathbb{Z}$$

时也会达到最大值。这意味着频率$f_d$和$f_d+n{f}_{PRF}$无法区分，导致速度模糊。

C. 最小二乘法

给定线性模型$AX=B+E$，其中$E$是噪声向量。最小二乘问题是：

$$\underset{X}{\min }\Vert AX-B{\Vert }^2=\underset{X}{\min }(AX-B{)}^T(AX-B)$$

展开目标函数：

$$J(X)=X^T{A}^{T}AX-2X^T{A}^{T}B+B^{T}B$$

对$X$求导并令其等于零：

$$\frac{\partial J}{\partial X}=2A^{T}AX-2A^{T}B=0$$

得到正规方程：

$$A^{T}AX=A^{T}B$$

当$A^{T}A$可逆时（通常在$N_f\ge 2$时成立），解为：

$$X=(A^{T}A{)}^{-1}{A}^{T}B=A^{†}B$$

对于我们的距离变化率估计问题，$A^{T}A$的具体形式为：

$$A^{T}A=\left[\begin{array}{cc}{\sum }_{k=0}^{N_f-1}(k{T}_f{)}^2& {\sum }_{k=0}^{N_f-1}k{T}_f\\ {\sum }_{k=0}^{N_f-1}k{T}_f& N_f\end{array}\right]$$

利用求和公式：

$$\sum _{k=0}^{N_f-1}k=\frac{N_f(N_f-1)}{2}$$

$$\sum _{k=0}^{N_f-1}{k}^2=\frac{N_f(N_f-1)(2N_f-1)}{6}$$

可以得到$(A^{T}A{)}^{-1}$的解析表达式，从而直接计算距离变化率$\dot{v}$。

D. 模糊参数估计的最优性分析

定义估计误差为：

$$e(N)=|\hat{v}+N\times 2v_{max}-\dot{v}|$$

考虑噪声影响，假设$\dot{v}=v_{true}+\eta$，其中$\eta \sim \mathcal{N}(0,{\sigma }^2)$是高斯噪声。

正确的模糊参数为$N_0$，满足：

$$v_{true}=\hat{v}+N_0\times 2v_{max}$$

则误差函数变为：

$$e(N)=|(\hat{v}+N\times 2v_{max})-(\hat{v}+N_0\times 2v_{max}+\eta )|$$
$$=|(N-N_0)\times 2v_{max}-\eta |$$

当$|\eta |<v_{max}$时（这在实际中通常满足），最小化$e(N)$会正确选择$N=N_0$。

错误选择$N\ne N_0$的概率为：

$$P_{error}=P(|\eta |>v_{max})=2Q\left(\frac{v_{max}}{\sigma }\right)$$

其中$Q(\cdot )$是高斯Q函数。这表明增加帧数$N_f$可以减小$\sigma$，从而降低错误概率。

E. MIMO系统中的速度模糊加剧

在$N_t$个发射天线的时分MIMO系统中，有效的啁啾间隔变为：

$$T_l^{MIMO}=N_t\times T_l$$

相应的最大无模糊速度降低为：

$$v_{max}^{MIMO}=\frac{\lambda }{4T_l^{MIMO}}=\frac{v_{max}^{SISO}}{N_t}$$

例如，对于双发射天线系统（$N_t=2$），最大无模糊速度减半，从9.73 m/s降至4.87 m/s。这大大增加了正常交通场景中出现速度模糊的概率，凸显了本文提出的速度消歧方法的重要性。