SAR信号处理重要工具-傅里叶变换(二)
本文系统介绍了傅里叶变换在SAR信号处理中的应用,重点分析了三种典型信号的变换特性:1)推导了矩形信号、单频信号和线性调频信号的傅里叶变换公式;2)通过仿真验证了离散傅里叶变换与理论结果的幅度差异和相位特性;3)针对不同信号类型,给出了脉宽、带宽、调频率等关键参数的估计方法。研究结果表明,傅里叶变换能有效分析信号频域特性,为SAR信号处理提供了重要工具。
系列文章目录
文章目录
目录
前言
本文详细推导了矩形脉冲信号、单频脉冲信号以及线性调频率信号的离散傅里叶变换结果,并结合仿真对比了理论公式与实际结果的幅度差异以及相位差异,并基于FFT实现对这三类信号关键参数的估计。
一、傅里叶变换及离散傅里叶变换
1.1、傅里叶变换
模拟信号傅里叶变换为:
对应的逆变换为:
其中为模拟频率,模拟信号
的频谱是信号频谱分析最终想得到的。
1.2、离散傅里叶变换
对离散信号周期化得:
对离散周期信号傅里叶变换得
对应的逆变换:
由定义有:
二、常见信号的变换结果
2.1、矩形信号
考虑矩形信号为
其中表示信号持续时间,
由公式(1)可以得到矩形信号傅里叶变换结果为
考虑,因此
由公式(1),当时,
,能够快速验证了公式(9)的幅度正确性。
考虑离散矩形信号是由公式(7)采样获得,采样率,采样间隔为
,采样点数为
,信号持续点数
,由公式(4)得到离散矩形信号的离散傅里叶变换结果为
由等比数列求和公式可得
由公式(9)和公式(11)可以看出傅里叶变换结果和离散傅里叶变换结果的幅度相差,此外离散傅里叶变换信号的起始时刻默认为0,与模拟信号的起始时刻无关,因此公式(11)的结果包含模拟信号起始时刻不为0带来的固定相位项。
2.2、单频信号
考虑单频脉冲信号
其中为频率,
表示信号持续时间,
由公式(1)可以得到单频脉冲信号傅里叶变换结果为
考虑,因此
由公式(1),当时,
,能够快速验证了公式(13)的幅度正确性。
考虑离散矩形信号是由公式(7)采样获得,采样率,采样间隔为
,采样点数为
,信号持续点数
,由公式(4)得到离散矩形信号的离散傅里叶变换结果为
由等比数列求和公式可得
由公式(14)和公式(16)可以看出傅里叶变换结果和离散傅里叶变换结果的幅度相差,此外离散傅里叶变换信号的起始时刻默认为0,与模拟信号的起始时刻无关,因此公式(11)的结果包含模拟信号起始时刻不为0带来的固定相位项。对比公式(11)和公式(16),发现信号频谱发生了频移现象,初步验证了傅里叶变换的频移性质。
2.3、线性调频信号
考虑线性调频脉冲信号
其中为调频率参数,
表示信号持续时间,
由公式(1)可以得到线性调频脉冲信号傅里叶变换结果为
积分相位表达式为:
积分相位求导置零,求解信号幅度平稳时的时频耦合关系
得到
将积分相位在
处进行泰勒展开,忽略高阶项得
根据驻定相位原理,积分接近于0,积分时间t在附近取值才能有效积分,因此
令,则
令,
,则
令正弦菲涅尔积分,正弦菲涅尔积分
,
。
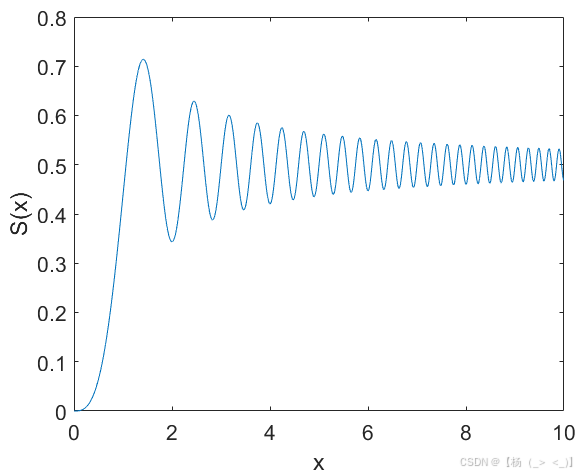
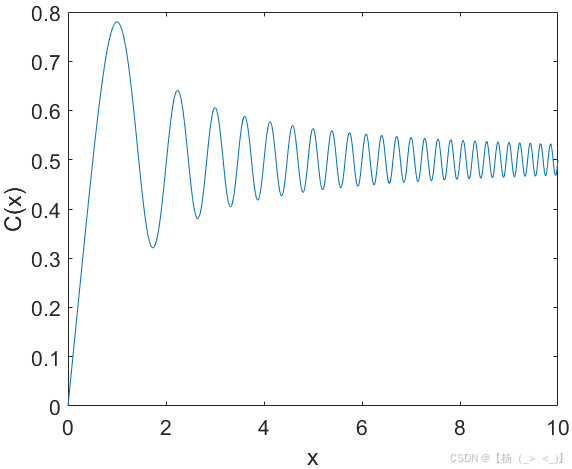
,当
时,
,
则
其中信号带宽。
时域能量,频域能量
,两者相等,满足帕塞瓦尔定理,进一步验证公式的正确性。
考虑离散傅里叶变换与傅里叶变换幅度相差,时延相差
,则公式(17)的离散信号的离散傅里叶变换结果为
三、仿真分析
2.1、矩形信号
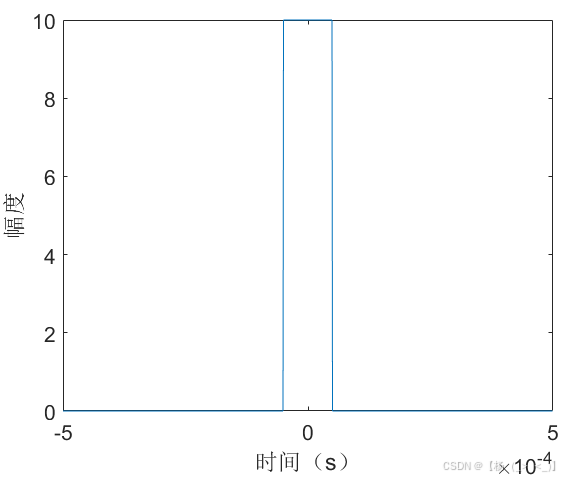
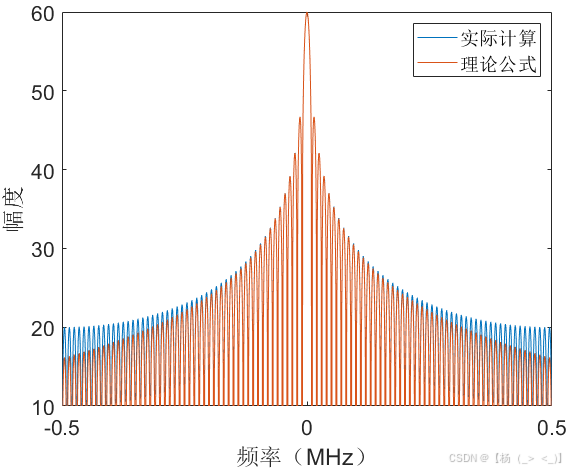
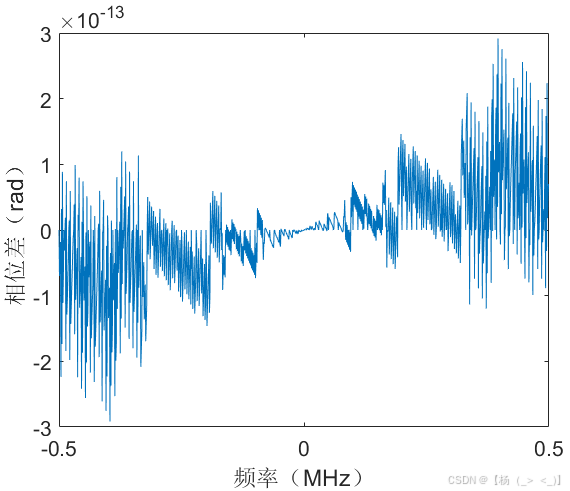
(a)时域 (b)频域 (c) 相位差
考虑数据时长1 ms,矩形脉冲信号位于数据中心时刻,幅度10,持续时长100 us,信号采样率1 MHz,信号时域图如上图(a)所示,图(b)展示了matlab中fft实际计算结果与公式(11)的频谱对比,可以看出在峰值频点处信号频谱高度重合,图(c)展示了理论与实际结果的相位差,可以看出相位差几乎为0。由信号3db带宽定义可以估计获得脉宽估计值为98 us,由频谱峰值进一步计算获得幅度估计值为10.2。下图展示了10dB信噪比下的对比结果,某次实验估计的脉宽值为127 us,幅度估计值为8.5。
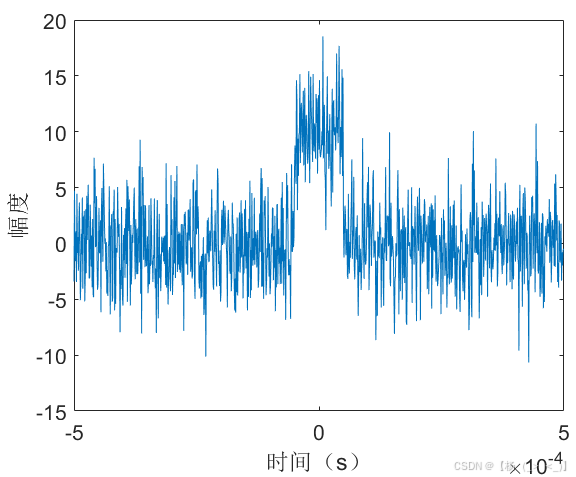
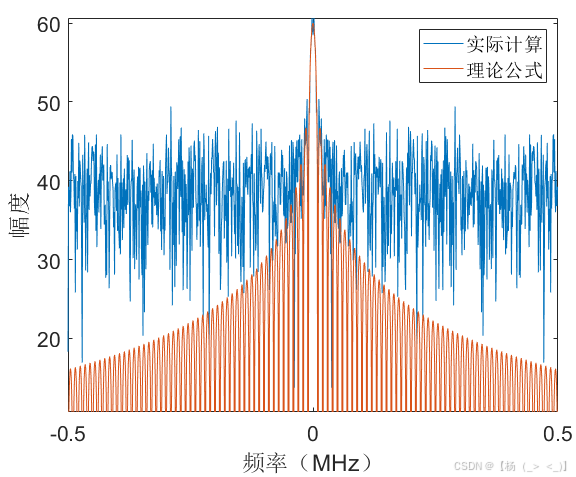
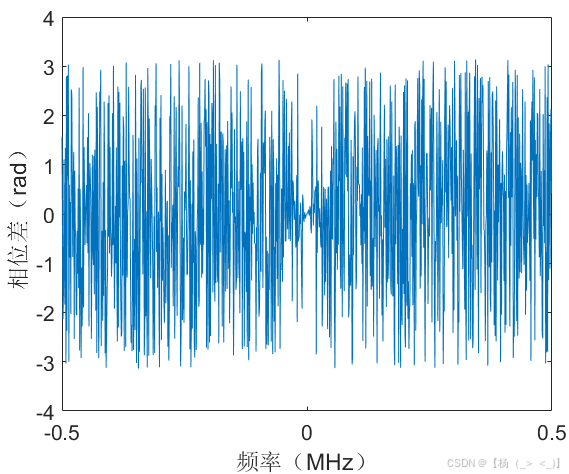
(a)时域 (b)频域 (c) 相位差
2.2、单频信号
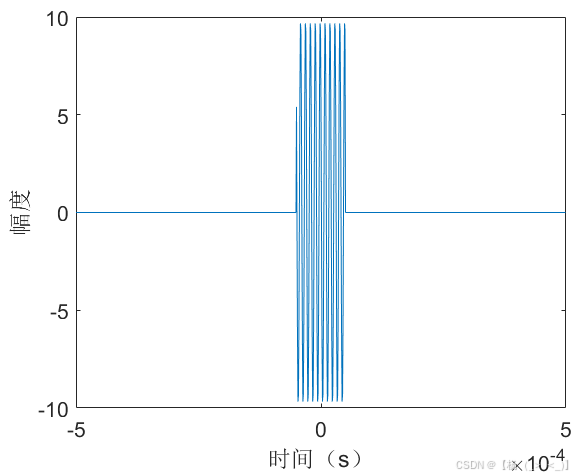
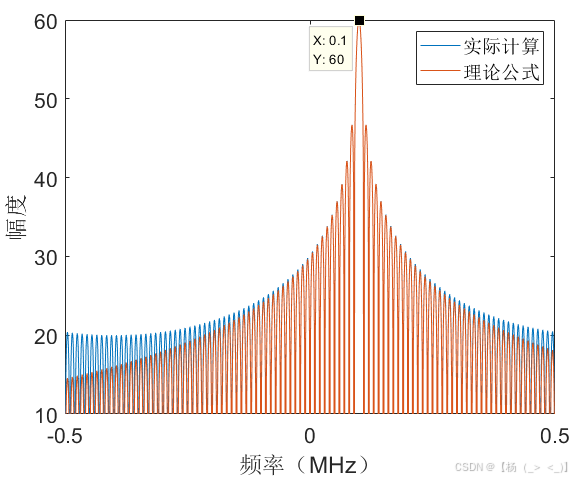
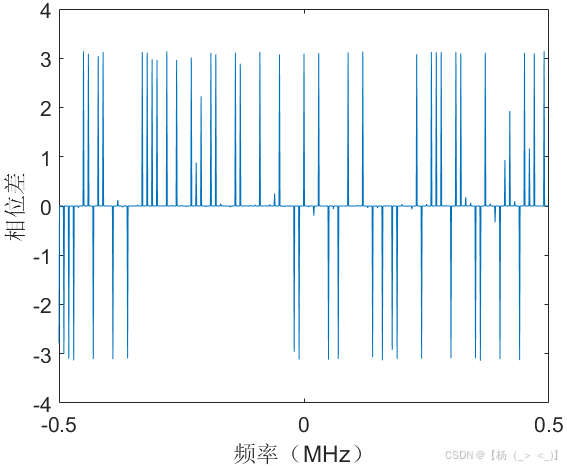
(a)时域 (b)频域 (c) 相位差
考虑数据时长1 ms,单频脉冲信号位于数据中心时刻,幅度10,频率100 KHz,初相1rad,持续时长100 us,信号采样率1 MHz,信号时域图如上图(a)所示,图(b)展示了matlab中fft实际计算结果与公式(16)的频谱对比,可以看出在峰值频点处信号频谱高度重合,图(c)展示了理论与实际结果的相位差,可以看出相位差存在倒问题。由信号3db带宽定义可以估计获得脉宽估计值为98 us,由频谱峰值进一步计算获得幅度估计值为10.2,频率估计值为100 KHz,初相估计值为1.00 rad。下图展示了10dB信噪比下的对比结果,某次实验估计的脉宽值为127 us,幅度估计值为8.8,频率估计值为100 KHz,初相估计值为0.96 rad。
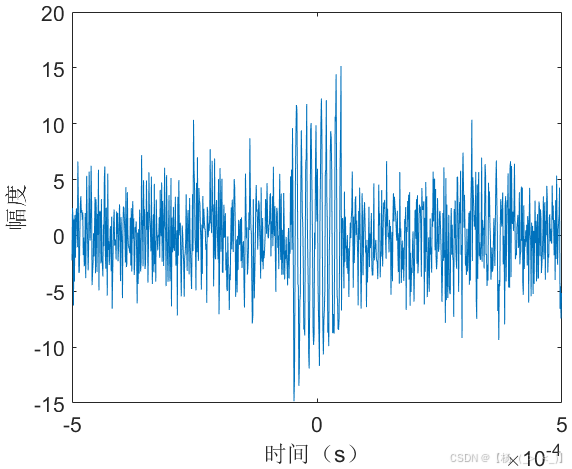
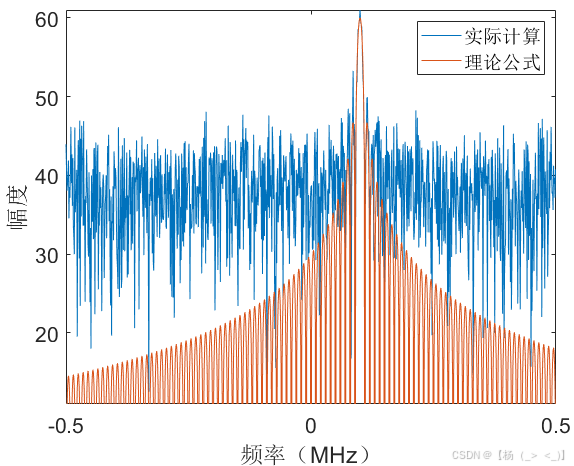
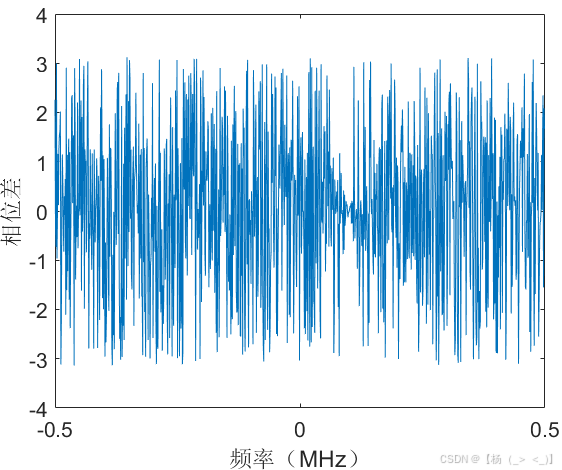
(a)时域 (b)频域 (c) 相位差
2.3、线性调频信号
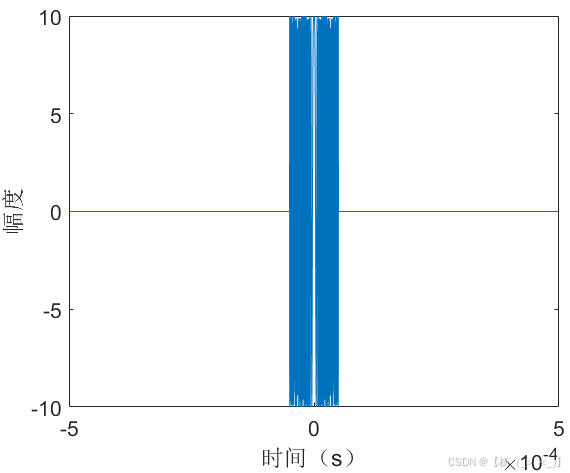
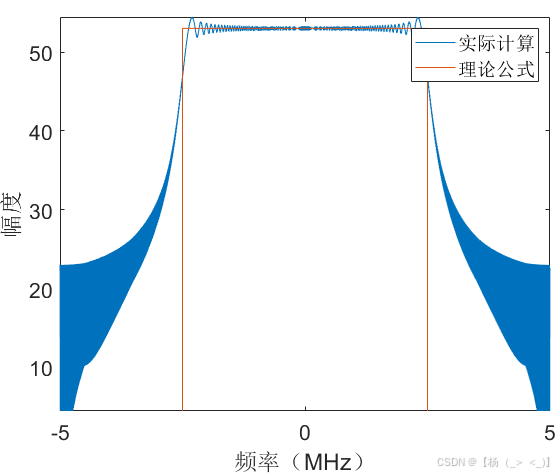
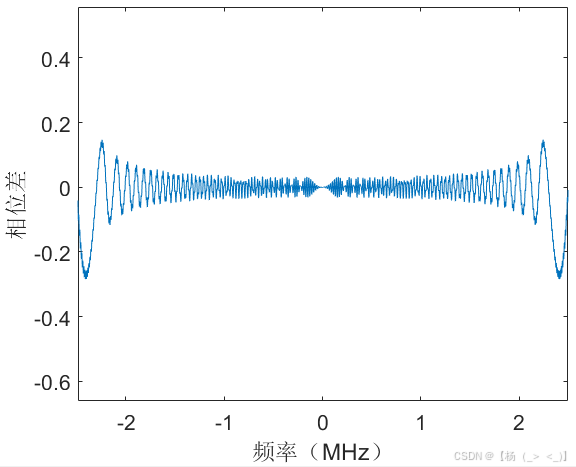
(a)时域 (b)频域 (c) 相位差
考虑数据时长1 ms,单频脉冲信号位于数据中心时刻,幅度10,信号带宽 5MHz,持续时长100 us,调频率为50 GHz/s,信号采样率10 MHz,信号时域图如上图(a)所示,图(b)展示了matlab中fft实际计算结果与公式(16)的频谱对比,可以看出在带宽内信号频谱高度重合,图(c)展示了理论与实际结果的相位差,可以看出相位差很小,进一步验证公式(27)相位项的准确性。由信号3db带宽定义可以估计获得脉宽估计值为99.9 us,带宽估计值为5.001 MHz,调频率估计值为50.06 GHz/s,由带宽内平均频谱值进一步计算获得幅度估计值为10.04。下图展示了30dB信噪比下的对比结果,某次实验脉宽估计值为99.9 us,带宽估计值为4.780 MHz,调频率估计值为47.85 GHz/s,由带宽内平均频谱值进一步计算获得幅度估计值为9.91。
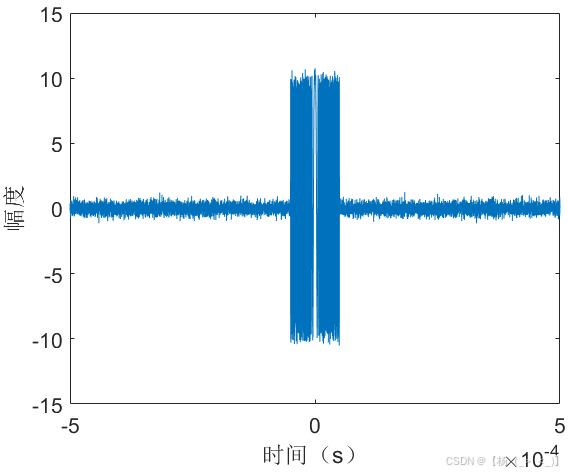
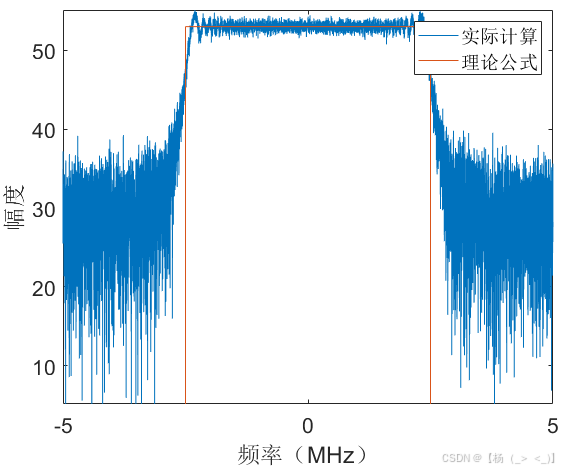
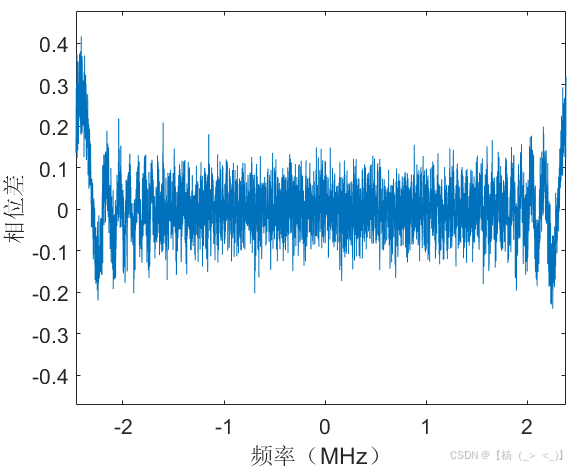
(a)时域 (b)频域 (c) 相位差
总结
本文主要介绍傅里叶变换及离散傅里叶变换前后幅度规律,分析了三种典型信号(矩形信号、单频信号和线性调频信号)的变换特性,推导了各自的傅里叶变换公式,并通过仿真验证了变换结果的幅度规律。转载请附上链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)