多径效应对汽车MIMO雷达DOA估计的MCRB性能界定

M. Levy-Israel, I. Bilik and J. Tabrikian, “MCRB on DOA Estimation for Automotive MIMO Radar in the Presence of Multipath,” in IEEE Transactions on Aerospace and Electronic Systems, vol. 59, no. 5, pp. 4831-4843, Oct. 2023, doi: 10.1109/TAES.2023.3285861.

摘要

自动驾驶与高级主动安全功能对车载传感系统提出了极高的要求，即必须具备高分辨率且精准的感知能力。汽车雷达，作为全天候工作的核心传感器，其性能直接关系到行车安全。然而，在实际道路环境中，雷达信号会受到来自路面、护栏等平坦表面的反射，形成多径传播。这种现象会导致到达角（DOA）的估计精度显著下降。多径的存在使得估计器所依赖的理想信号模型与实际接收到的复杂信号模型之间产生“失配”（misspecification）。传统的性能评估工具，如克拉默-拉奥界（CRB），因其假设模型与真实情况完全匹配，无法可靠地预测在这种失配情况下的性能退化。

本文的核心贡献在于，针对估计器在设计时忽略了多径效应这一普遍存在的场景，推导了失配克拉默-拉奥界（Misspecified Cramér-Rao Bound, MCRB）。MCRB能够量化并预测由于模型失配所带来的性能损失。文章不仅建立了MCRB与传统CRB之间的解析关系，还深入探究了多径如何导致DOA估计性能的退化。研究结果证明，MCRB能够可靠地预测失配最大似然估计器（MML）的渐近性能，从而为汽车雷达的性能评估和系统设计提供了一个更为现实和有效的理论工具。

I. 引言

现代汽车的感知套件是雷达与摄像头的深度融合。摄像头提供丰富的纹理和颜色信息，而雷达则凭借其穿透雨、雪、雾的能力，保障了在恶劣光照和天气条件下的可靠感知。自动驾驶车辆必须能够在各种复杂场景下安全运行，如城市峡谷、隧道、桥梁下等，而这些场景无一例外都存在显著的多径传播。特别是对于通常安装在车辆保险杠后方、非常接近地面的汽车雷达而言，来自路面的高程多径是一个持续存在的挑战。

当多径信号与目标直接回波信号在时间和频率上无法被雷达分辨（即落在同一个距离-多普勒单元内）时，它们会发生相干叠加。这种叠加可能是建设性的，即相位相同或相近，使得信号能量增强，有助于目标检测；也可能是破坏性的，即相位相反或相近，导致信号能量削弱甚至完全抵消，极大地恶化了目标的检测和定位精度。

克拉默-拉奥界（CRB）因其计算的便捷性和在理想条件下的可达性，被广泛用作评估参数估计性能的基准。然而，CRB的理论基础是估计器所用的模型必须与数据的真实生成模型完全一致。在多径场景下，若估计器仍使用无多径的理想模型，CRB便会失效，给出过于乐观的性能预测。为了解决这一问题，MCRB理论应运而生，它专门用于分析当估计器假设模型与数据真实模型不一致时的性能下界。本文的工作正是将MCRB理论应用于汽车MIMO雷达的DOA估计问题，并利用它来系统地评估各种关键参数，如间接路径的角度、天线波束宽度、地表反射系数等，对雷达性能的具体影响，旨在为设计能够更好应对多径挑战的新一代雷达系统提供坚实的理论指导。

II. 问题建模

我们考虑一个单基MIMO雷达系统，其天线阵列由$M_t$个发射单元和$M_r$个接收单元组成。在存在多径反射的场景中，雷达接收到的回波信号由直接路径分量和间接路径分量构成。

1. 信号模型

• 直接路径信号 ($z_{d,k}$)
  这是从雷达发射，直接到达目标，再由目标直接反射回雷达的信号。对于第k个处理周期（如一个chirp），其数学模型可以表示为：
  $$z_{d,k}(t)\triangleq {\alpha }_d{e}^{j{\omega }_{D_d}kT}A(\theta )p(t-{\tau }_d),t\in [0,T]$$
  其中，${\alpha }_d$是包含双程路径损耗和相位的复数幅度，${\omega }_{D_d}$是目标的多普勒角频率，$\theta$是目标的真实DOA，$A(\theta )=a_r(\theta )a_t^T(\theta )$是MIMO雷达在$\theta$方向上的导向矩阵（由接收和发射导向矢量构成），$p(t-{\tau }_d)$是带有时间延迟${\tau }_d$的发射波形。

• 间接路径信号 ($z_{i,k}$)
  这是信号经过一次或多次反射后到达接收机的分量。本文主要考虑一次反射，例如“雷达-反射面-目标-雷达”或“雷达-目标-反射面-雷达”。这两条路径的物理特性（如长度、反射材质）相同，可以合并建模为：
  $$z_{i,k}(t)\triangleq {\alpha }_i{e}^{j{\omega }_{D_i}kT}\overline{A}(\theta ,\psi )p(t-{\tau }_i)$$
  其中，${\alpha }_i$是间接路径的复数幅度，$\psi$是反射路径的DOA，$\overline{A}(\theta ,\psi )\triangleq a_r(\psi )a_t^T(\theta )+a_r(\theta )a_t^T(\psi )$是间接路径的等效导向矩阵。

2. 模型失配

• 真实数据模型 ($g_x$)
  雷达在现实中接收到的信号是上述两个分量与加性噪声$w_k(t)$的总和：
  $$x_k(t)=z_{d,k}(t)+z_{i,k}(t)+w_k(t)$$

• 假设数据模型 ($f_x$)
  然而，一个不考虑多径效应的常规估计算法，其内部所依赖的信号模型是简化的，只包含直接路径和噪声：
  $$x_k(t)=z_{d,k}(t)+w_k(t)$$

这种真实模型与假设模型之间的差异，就是本文所研究的模型失配。我们的目标是评估在这种失配条件下，对未知参数矢量 ξ = [ R e { α d } , I m { α d } , τ d , ω D d , θ ] T \xi = [Re\{\alpha_d\}, Im\{\alpha_d\}, \tau_d, \omega_{D_d}, \theta]^T ξ=[Re{αd​},Im{αd​},τd​,ωDd​​,θ]T 进行估计的理论性能下界。

III. MCRB 推导

MCRB为在模型失配情况下，对参数进行估计所能达到的均方误差（MSE）提供了一个下界。其通用形式包含两个部分：

$${\mathbb{E}}_g[(\hat{\xi }-\xi )(\hat{\xi }-\xi {)}^T]\ge \underset{\text{协方差贡献}}{\underbrace{C_D^{-1}(\xi )J_{(g,f)}(\xi )C_D^{-1}(\xi )}}+\underset{\text{偏置贡献}}{\underbrace{(\xi -{\xi }_A)(\xi -{\xi }_A{)}^T}}$$

第一项是协方差贡献，描述了估计值在均值附近的随机波动。第二项是偏置贡献，源于模型失配导致估计结果会系统性地偏离真实值$\xi$，收敛到一个有偏的值${\xi }_A$。

在本问题中，由于失配仅存在于信号的均值部分（即多了$z_{i,k}(t)$），而噪声的统计特性（协方差矩阵）被假设为是已知的，失配费雪信息矩阵（MFIM）$J_{(g,f)}(\xi )$可以简化为常规的费雪信息矩阵（FIM）$J(\xi )$。经过一系列复杂的矩阵求导和代数运算（详见附录），并做出“直接路径和间接路径的距离差与多普勒差远小于雷达分辨率”这一合理假设后，我们得到了DOA估计的MCRB解析表达式：

$$MCRB(\theta )=M_{\theta \theta }+B_{\theta \theta }$$

其中，协方差项$M_{\theta \theta }$和偏置项$B_{\theta \theta }$的具体形式为：

M θ θ = C R B ( θ ) E A ˙ ( ∣ t r ( A ˙ d H A i ) ∣ 2 + S M R ⋅ E A ˙ ) ( R e { t r ( A ˙ d H A i ) e − j Δ ϕ } − S M R E A ˙ ) 2 M_{\theta\theta} = CRB(\theta)\frac{E_{\dot{A}}(|tr(\dot{A}_{d}^{H}A_{i})|^{2}+SMR \cdot E_{\dot{A}})}{(Re\{tr(\dot{A}_{d}^{H}A_{i})e^{-j\Delta\phi}\}-\sqrt{SMR}E_{\dot{A}})^{2}} Mθθ​=CRB(θ)(Re{tr(A˙dH​Ai​)e−jΔϕ}−SMR ​EA˙​)2EA˙​(∣tr(A˙dH​Ai​)∣2+SMR⋅EA˙​)​

$$B_{\theta \theta }=(\theta -{\theta }_A{)}^2$$

这里的$CRB(\theta )$是在无多径干扰时的常规克拉默-拉奥界。公式揭示了MCRB与常规CRB的关系，并显示其性能受到信噪比（SNR）、**信号与多径功率比（SMR）以及两者之间的相位差（$\Delta \varphi$）**的共同影响。

为了验证该公式的自洽性，我们考察了两个极端情况：

1. 无多径时 (${\alpha }_i=0,SMR\to \infty$) ：此时，偏置项为零，协方差项$M_{\theta \theta }$收敛于$CRB(\theta )$。这意味着$MCRB(\theta )$正确地退化为常规的CRB，符合物理直觉。
2. 完全相干叠加时 (${\alpha }_i={\alpha }_d,\psi =\theta ,SMR=1$) ：此时直接路径和两个间接路径完全同相，信号幅度增强为原来的3倍，等效信噪比提升了9倍。推导结果显示，此时偏置项也为零，而$MCRB(\theta )=\frac{1}{9}CRB(\theta )$，精确地反映了信噪比提升9倍（即$10{\log }_{10}(9)\approx 9.54$ dB）所带来的性能改善。

IV. MCRB 数值评估与分析

本节通过仿真实验，直观展示MCRB的特性，并将其应用于分析实际的汽车场景。仿真环境设定为一个3发4收的MIMO雷达，构成一个12单元的虚拟均匀线阵。

---

图2: MCRB、CRB与估计器RMSE性能对比

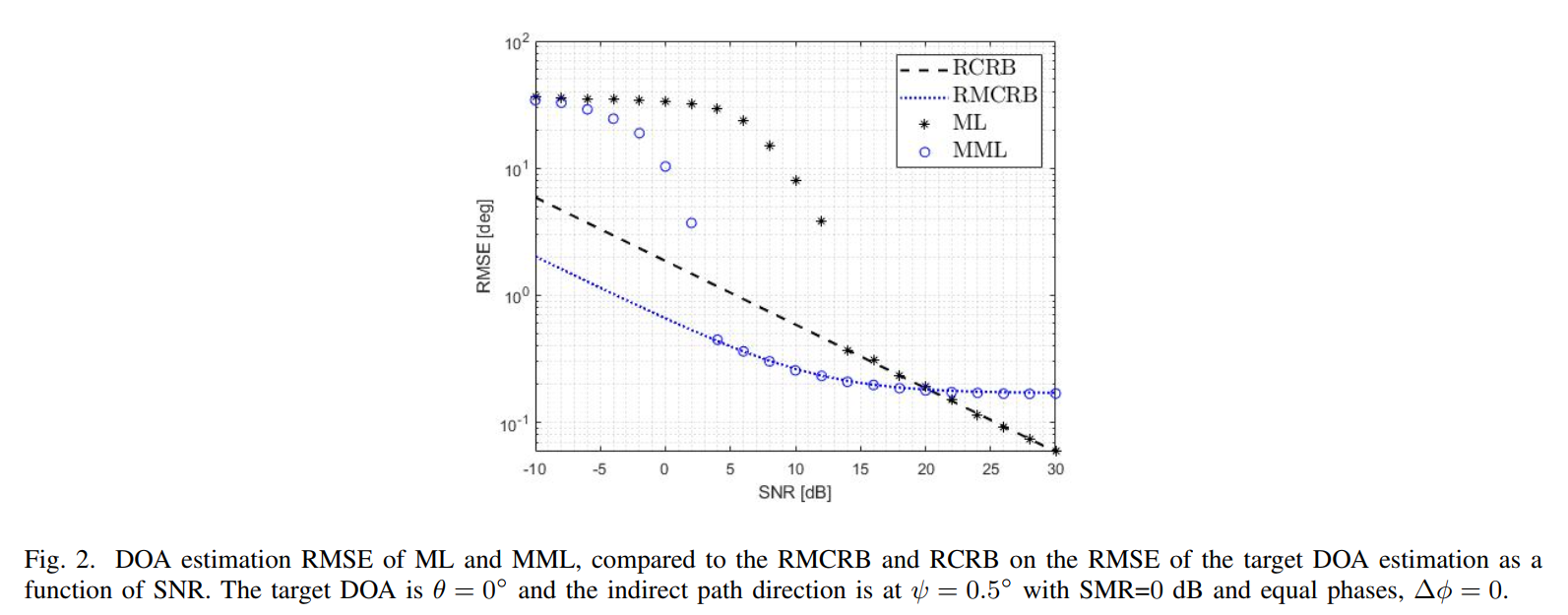
图片描述: 该图的横轴为信噪比（SNR），纵轴为DOA估计的均方根误差（RMSE），单位为度。图中包含了四条曲线：RCRB（虚线）、RMCRB（点线）、ML估计器RMSE（星号）和MML估计器RMSE（圆圈）。

分析与解读:

• MCRB的准确性: RMCRB曲线（点线）与MML估计器（圆圈）的实际性能高度吻合。这证明了MCRB能够精确预测在模型失配情况下的估计性能。
• 偏置效应与性能平台: 在高SNR区域（>20dB），MML的RMSE不再下降，而是趋于一个恒定的“性能平台”（error floor）。这是因为此时随机噪声的影响已经很小，误差主要由模型失配引入的系统性偏置决定。RMCRB准确地捕捉到了这个平台，而RCRB（虚线）则持续下降，给出了一个过于乐观且不切实际的性能预测。
• 建设性干涉的益处: 在SNR低于20dB时，RMCRB甚至低于RCRB。这是因为仿真设置中，直接路径和间接路径的角度非常接近（$\Delta \theta =0.5^{\circ }$），发生了建设性干涉，等效地增强了接收信号的能量，从而暂时提高了估计精度。

---

图3: DOA差异对RMCRB的影响

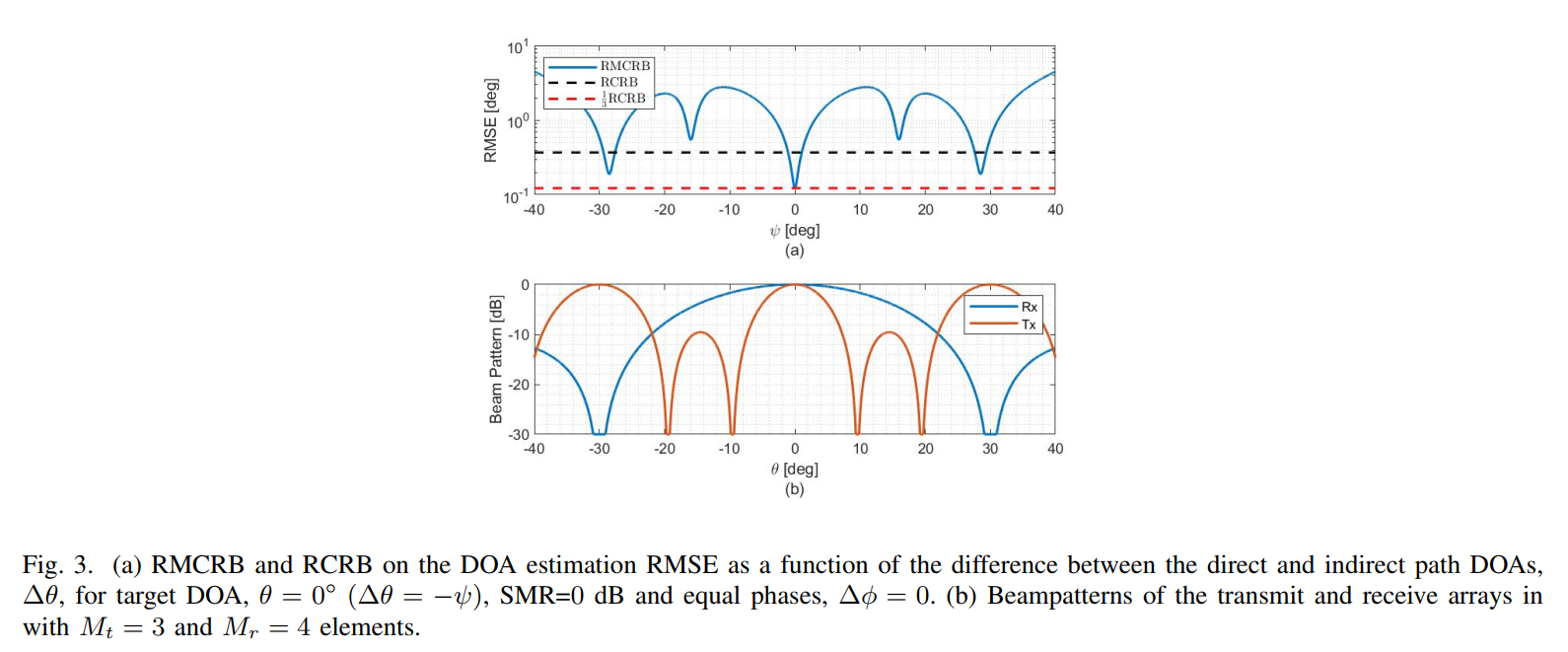
图片描述: 上图(a)展示了当直接路径和间接路径的DOA差异$\Delta \theta$从-40度变化到+40度时，RMCRB（蓝色实线）的变化情况，并与两种CRB（黑色和红色虚线）进行对比。下图(b)是该雷达的接收（Rx）和发射（Tx）天线方向图。

分析与解读:

• 当$\Delta \theta =0$时（即多径与目标同向），性能最好，RMSE达到最小值，因为此时信号干涉是完全建设性的。
• 随着$|\Delta \theta |$在主瓣内增大，性能逐渐变差。
• 一个有趣的现象是，在$\psi =\pm 30^{\circ }$处，RMSE出现了显著的局部极小值。通过对比图(b)可以发现，这恰好是发射阵列（Tx）的栅瓣位置。尽管接收阵列（Rx）在该角度有零点，但通过发射栅瓣接收到的多径信号依然对提高DOA估计精度产生了积极的贡献。

---

图4: SMR对RMCRB的影响

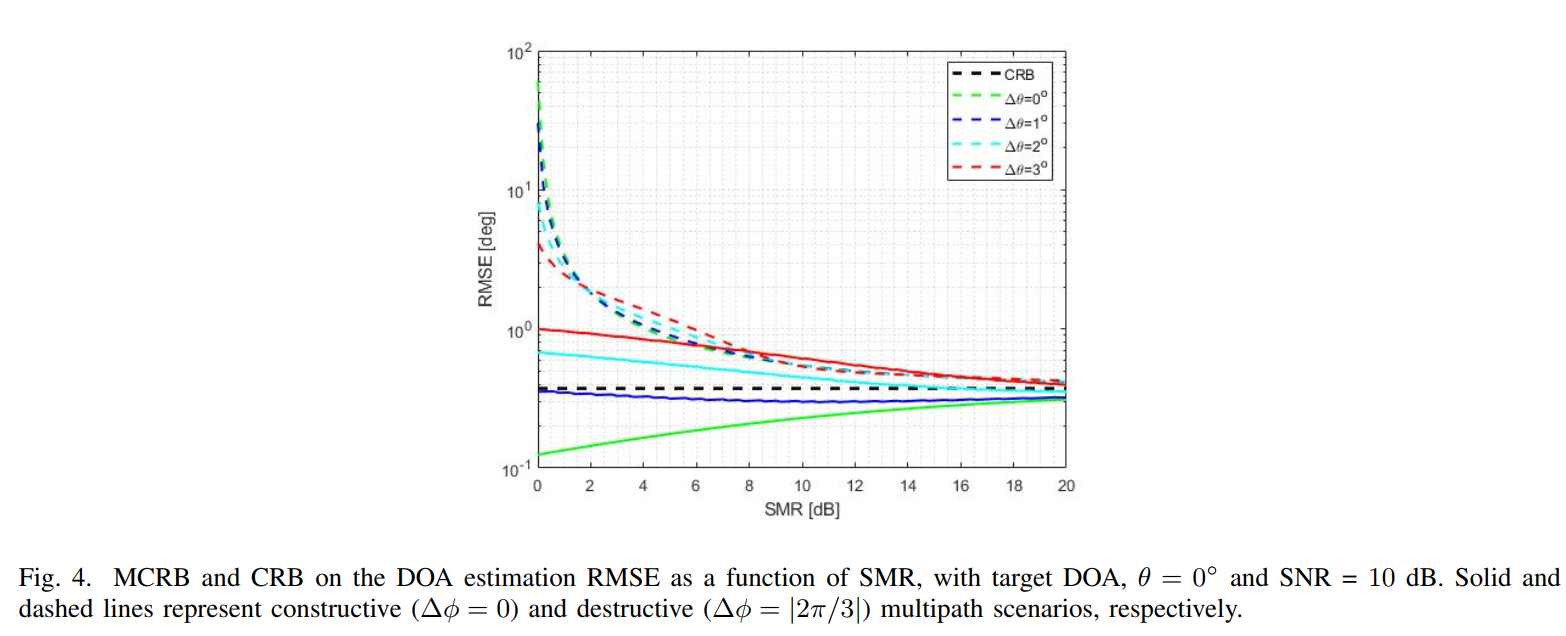
图片描述: 该图展示了在不同的DOA差异$\Delta \theta$下，RMCRB随SMR（信号与多径功率比）的变化。实线代表建设性干涉（$\Delta \varphi =0$），虚线代表破坏性干涉（$\Delta \varphi =2\pi /3$）。

分析与解读:

• 高SMR区域: 当SMR很高时（>15dB），意味着直接路径信号远强于多径信号，多径影响可以忽略不计。因此，所有曲线都收敛于无多径时的RCRB（黑色虚线）。
• 低SMR区域: 当SMR很低时，意味着多径信号占主导。此时性能主要由偏置决定，$\Delta \theta$越大，偏置越大，误差也越大。
• 破坏性干涉的危害: 对于破坏性干涉（虚线），在SMR接近0dB（即直接路径和间接路径能量相等）时，RMSE出现了剧烈的峰值。这表示信号能量被严重抵消，导致性能急剧恶化。

---

图5: 相位差和DOA差异的联合影响

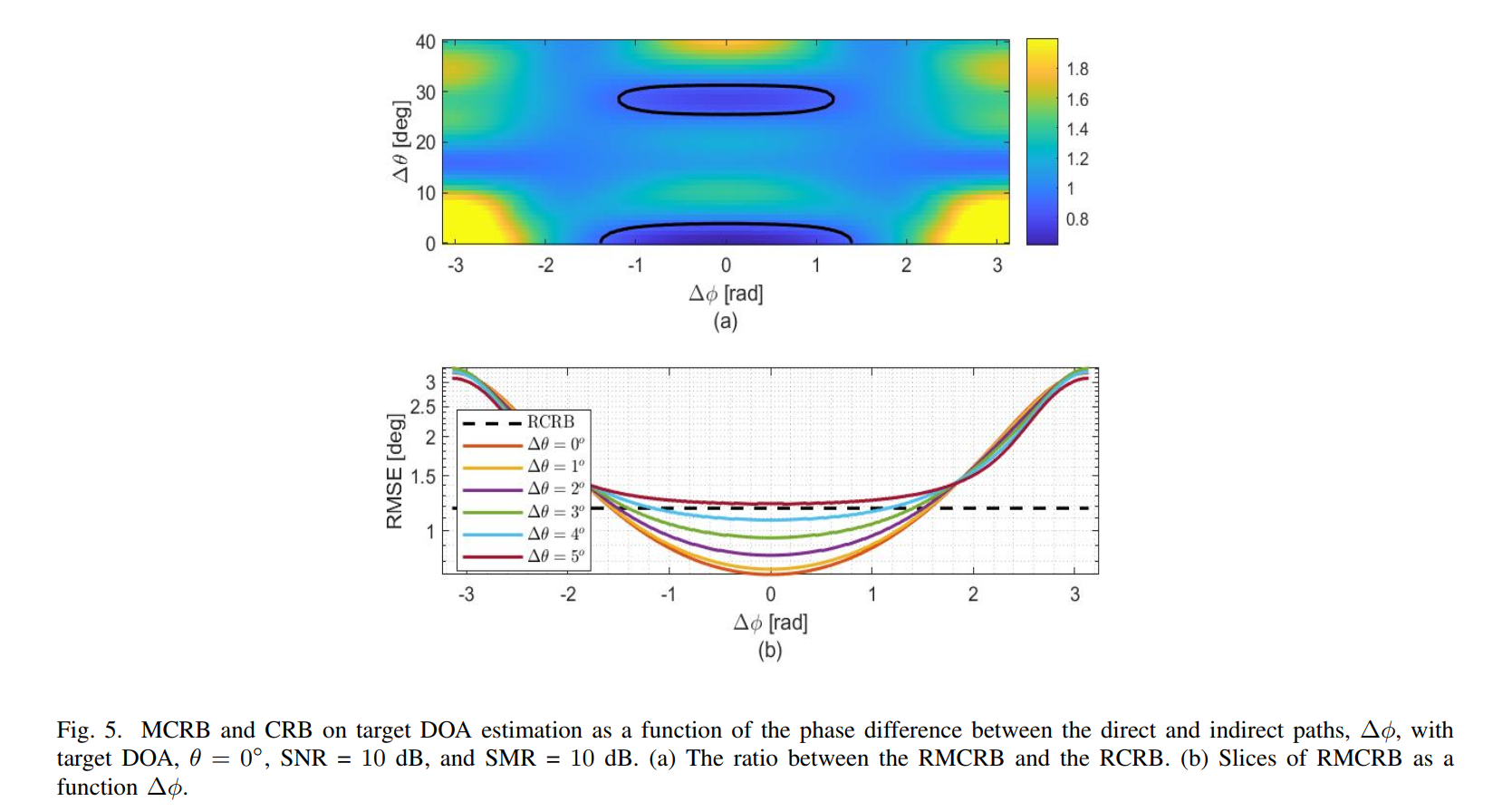
图片描述: 上图(a)是一个二维热力图，展示了RMCRB与RCRB的比值，颜色越冷（蓝色）表示比值越小，性能越好。横轴是相位差$\Delta \varphi$，纵轴是DOA差异$\Delta \theta$。图中黑色轮廓线圈出的区域代表RMCRB优于RCRB（比值<1）。

分析与解读: 这张图直观地揭示了多径何时有益、何时有害。在黑色轮廓线内部，即当DOA差异$|\Delta \theta |$较小（约小于$6^{\circ }$）且相位差$|\Delta \varphi |$也较小（约小于1.5弧度）时，多径实际上起到了增强信号的作用，是有益的。而在其他区域，多径则会导致性能下降。

---

图6 & 7 & 8: 典型汽车场景应用分析

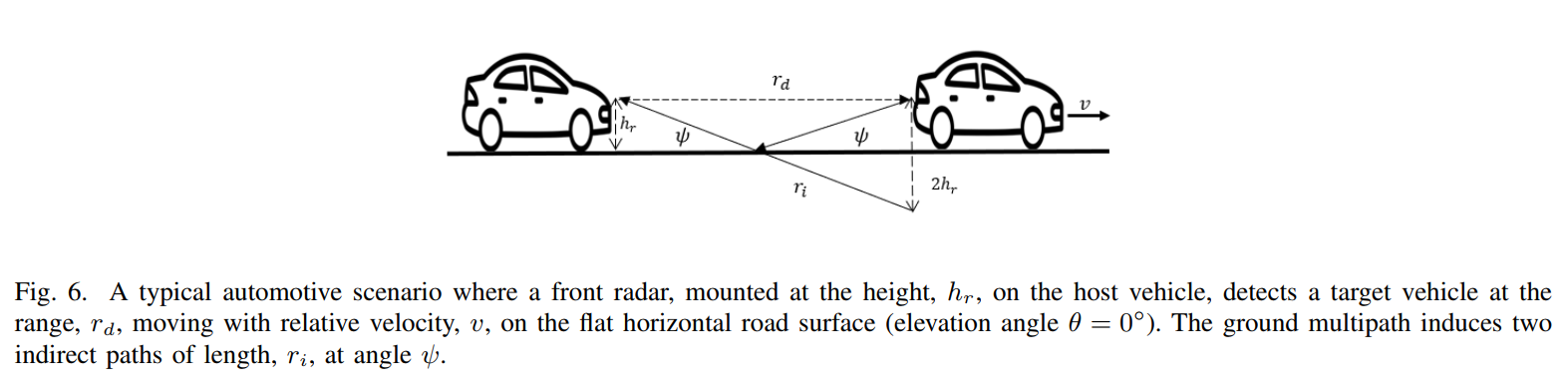
• 图6: 汽车场景几何模型 - 描绘了一个典型的汽车雷达场景：前向雷达安装在高度$h_r$处，探测距离为$r_d$的目标车辆。地面反射产生了间接路径，其几何关系（长度$r_i$和角度$\psi$）是确定的。

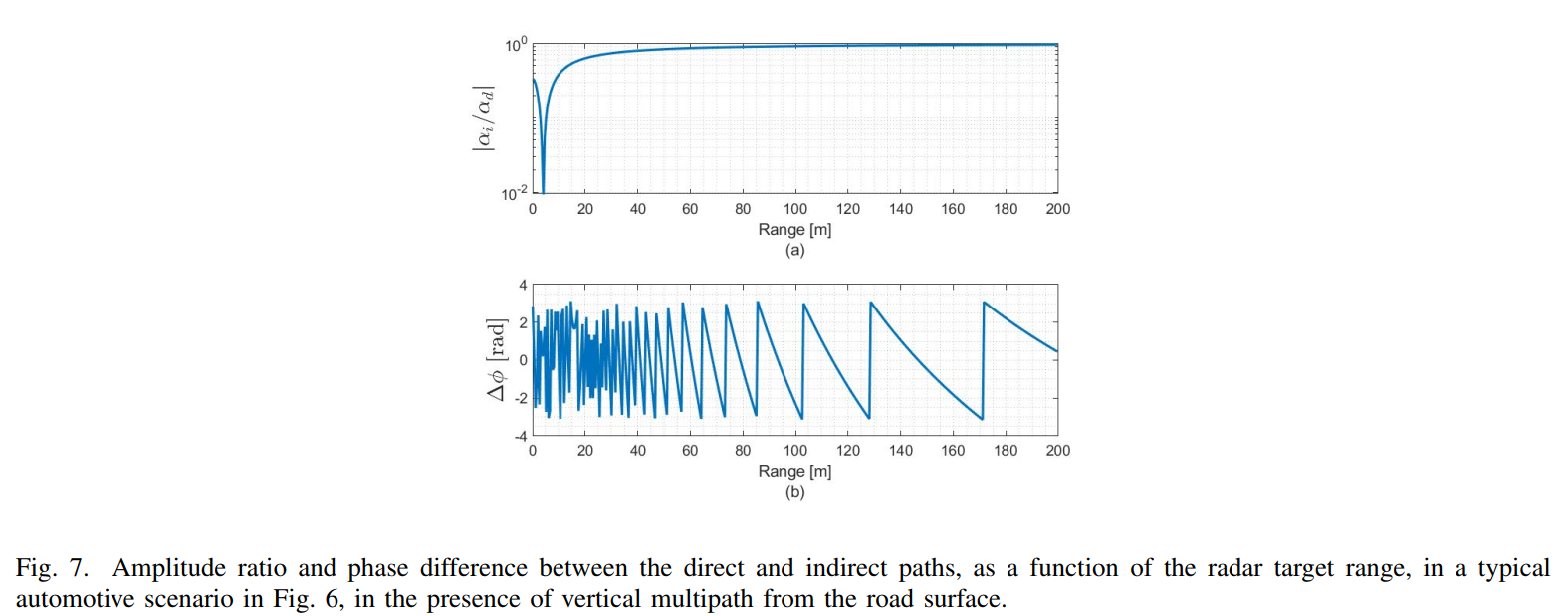
• 图7: 路径系数随距离的变化 - 基于干燥沥青路面的反射模型，计算了间接路径与直接路径的幅度比和相位差随目标距离的变化。在远距离，幅度比趋近于1，而相位差因路径长度差的变化而快速振荡。

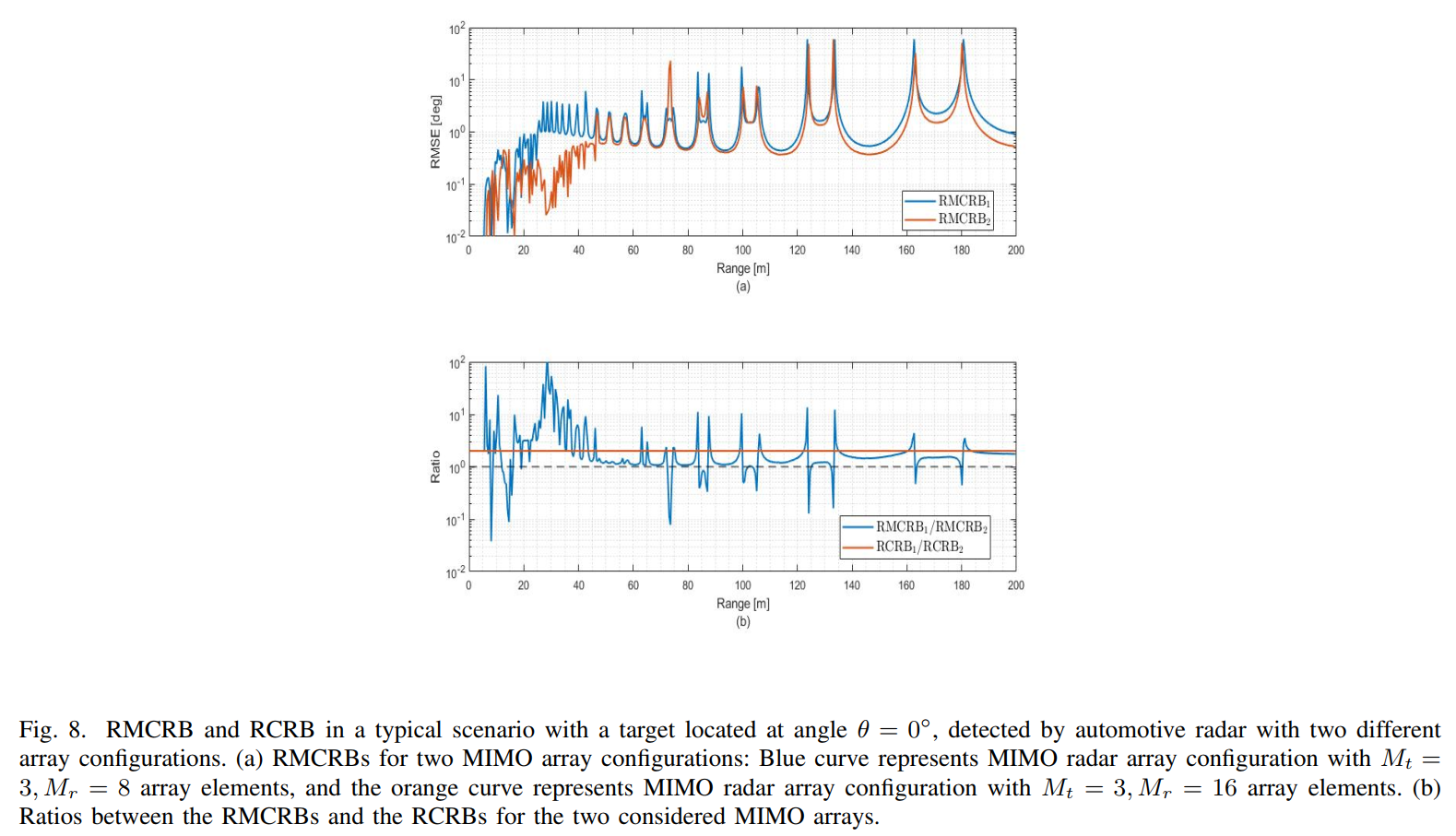
• 图8: 实际场景下DOA估计性能随距离的变化 - 这是本文最重要的应用结果之一。它展示了两种不同天线配置（蓝色：3发8收；橙色：3发16收）下，DOA估计的RMCRB随目标距离的变化。

分析与解读:

• 性能“盲区”: RMCRB曲线呈现出一系列周期性的尖峰。这些尖峰对应着特定的“盲区”距离，在这些距离上，直接路径和间接路径恰好形成破坏性干涉，导致RMSE急剧增大，性能严重恶化。
• 天线孔径的作用: 在短距离（<50m）内，目标和多径的角度差异较大，拥有更大孔径和更窄波束的3x16天线（橙色曲线）性能明显优于3x8天线。
• 大孔径的局限性: 然而，在长距离处，随着$\Delta \theta$趋近于0，两条路径在角度上变得不可分辨。此时，两种天线配置的性能趋于一致，增加天线孔径带来的性能提升微乎其微。这揭示了一个深刻的洞见：在实际尺寸限制下，对于长距离场景，仅仅通过增大天线阵列孔径，可能无法有效解决由地面反射引起的多径问题。

V. 结论

本文成功地将MCRB理论应用于分析汽车MIMO雷达在多径场景下的DOA估计性能问题。通过数学推导和详尽的仿真分析，得出了以下关键结论：

1. MCRB的有效性: 本文推导的MCRB能够预测当估计器忽略多径效应时的真实性能，揭示了传统CRB无法体现的由模型失配引起的偏置效应和性能平台。
2. 多径影响的量化: MCRB提供了一个强大的分析工具，能够量化SMR、相位差、角度差等关键因素对性能的综合影响，并预测由破坏性干涉引起的性能“盲区”。
3. 对系统设计的启示: 研究表明，在多径环境中，传统的设计思路（如单纯增大天线孔径）可能效果有限。MCRB可以作为指导，用于设计更具鲁棒性的雷达系统，例如通过优化天线阵列几何结构或开发能够感知并利用多径信息的先进信号处理算法。

---

附录：关键数学推导

这里展示原文中省略的部分数学推导，以揭示MCRB解析表达式的由来。

1. 矩阵 $C_D$ 的元素推导

MCRB的计算核心在于矩阵$C_D$。其元素 $[C_D{]}_{ij}$ 的通用计算公式为：
$$[C_D{]}_{ij}=[J(\xi ){]}_{ij}-\frac{2}{{\sigma }_w^2}Re\left\{\sum _{k=-\frac{K}{2}}^{\frac{K}{2}}{\int }_T\frac{{\partial }^2{z}_{d,k}^H}{\partial {\xi }_i\partial {\xi }_j}{z}_{i,k}dt\right\}$$
其中 $J(\xi )$ 是常规FIM，第二项是失配修正项。我们以对DOA估计至关重要的对角元素 $[C_D{]}_{55}$（对应参数$\theta$）为例：
$$[C_D{]}_{55}=J_{\theta \theta }-\frac{2}{{\sigma }_w^2}Re\left\{\sum _k{\int }_T\frac{{\partial }^2{z}_{d,k}^H}{\partial {\theta }^2}{z}_{i,k}dt\right\}$$
对 $z_{d,k}^H={\alpha }_d^{\ast }{e}^{-j{\omega }_{D_d}kT}{p}^H(t-{\tau }_d)A^H(\theta )$ 求关于$\theta$的二阶偏导，得到 $\frac{{\partial }^2{z}_{d,k}^H}{\partial {\theta }^2}={\alpha }_d^{\ast }{e}^{-j...}{p}^H(...){\ddot{A}}_d^H$。代入并利用信号的正交性，积分项可以简化，最终得到：
[ C D ] 55 = 2 K E p σ w 2 ( ∣ α d ∣ 2 E A ¨ − R e { α d ∗ α i t r ( A ¨ d H A i ) } ) [C_{D}]_{55} = \frac{2KE_p}{\sigma_w^2} \left(|\alpha_d|^2 E_{\ddot{A}} - Re\{\alpha_d^* \alpha_i tr(\ddot{A}_d^H A_i)\}\right) [CD​]55​=σw2​2KEp​​(∣αd​∣2EA¨​−Re{αd∗​αi​tr(A¨dH​Ai​)})
其中 $E_{\ddot{A}}=tr({\ddot{A}}_d{\ddot{A}}_d^H)$。类似地可以推导出所有其他元素。

2. 矩阵 $C_D$ 的简化

在假设直接路径和间接路径的距离差$\Delta r$和多普勒差$\Delta \omega$远小于雷达分辨率时，我们有以下关键近似：
$${\rho }_k(\Delta \omega )\triangleq {\alpha }_d^{\ast }{\alpha }_i{e}^{j\Delta \omega kT}\approx {\alpha }_d^{\ast }{\alpha }_i(\text{不依赖于k})$$
$$R_{pp}(\Delta \tau )=\int p(t-{\tau }_d)p^H(t-{\tau }_i)dt\approx E_p{I}_{M_t}(\text{近似正交})$$
这些近似使得$C_D$矩阵中大量的交叉项（如$\theta$与${\tau }_d$、${\omega }_{D_d}$的耦合项）由于对称求和等原因而变为零。这使得$C_D$矩阵呈现出一种更易于求逆的块结构。

3. $M_{\theta \theta }$ 的最终推导

经过简化后，$C_D$矩阵可以表示为 $C_D=\frac{2K{E}_p}{{\sigma }_w^2}Z$，其中$Z$是一个只与${\alpha }_d,{\alpha }_i,A_d,A_i$等物理参数相关的矩阵。
$M_{\theta \theta }$是矩阵$M=C_D^{-1}J{C}_D^{-1}$的右下角对角元素。通过对分块矩阵$Z$求逆，得到$Z^{-1}$，再与对角化的FIM矩阵$J$相乘，经过一系列繁琐但直接的代数运算，便可得到最终的解析表达式：
M θ θ = σ w 2 ( ∣ α i t r ( A ˙ d H A i ) ∣ 2 + ∣ α d ∣ 2 E A ˙ ) 2 K E p ( 2 R e { α d ∗ α i t r ( A ¨ d H A i ) } − ∣ α d ∣ 2 E A ˙ ) 2 M_{\theta\theta}=\frac{\sigma_{w}^{2}(|\alpha_{i}tr(\dot{A}_{d}^{H}A_{i})|^{2}+|\alpha_{d}|^{2}E_{\dot{A}})}{2KE_{p}(2Re\{\alpha_{d}^{*}\alpha_{i}tr(\ddot{A}_{d}^{H}A_{i})\}-|\alpha_{d}|^{2}E_{\dot{A}})^{2}} Mθθ​=2KEp​(2Re{αd∗​αi​tr(A¨dH​Ai​)}−∣αd​∣2EA˙​)2σw2​(∣αi​tr(A˙dH​Ai​)∣2+∣αd​∣2EA˙​)​
再利用 $CRB(\theta )=\frac{{\sigma }_w^2}{2K{E}_p|{\alpha }_d{|}^2{E}_{\dot{A}}}$ 和 $SMR=|{\alpha }_d{|}^2/|{\alpha }_i{|}^2$ 进行代换和整理，即可得到报告正文中给出的、形式更为直观的最终结果。