前言

在机器视觉和图像处理领域，图像噪点是影响后续分析精度的关键问题。无论是工业相机采集的产品图像、安防监控画面，还是日常拍摄的照片，都可能因设备性能、传输干扰、光照变化等因素产生噪声。

一、图像噪声基础概念

1.1 噪声定义与本质

图像噪声是指图像中存在的干扰有效信息的随机信号，表现为像素值与周围正常像素存在明显差异的离散点或区域。从本质上讲，噪声是图像采集、传输或处理过程中引入的无用信号，会导致图像清晰度下降、细节丢失，甚至影响后续的特征提取、目标检测等高级任务。

1.2 常见噪声类型

实际应用中，图像噪声主要分为两类，其特征和产生原因存在显著差异：

• 高斯噪声：噪声分布符合正态分布（高斯分布），表现为图像整体呈现均匀的颗粒感，使画面变得模糊。产生原因主要包括图像传感器的热噪声、光照不足导致的电子噪声，以及传输过程中的信道干扰。例如，在低光环境下使用手机拍摄的照片，常常会出现这种均匀的“雪花状”噪点。
• 椒盐噪声：又称脉冲噪声，表现为图像中随机分布的黑色（像素值接近0）或白色（像素值接近255）斑点，如同在图像上撒了一把盐和胡椒粉。其产生原因主要包括传感器故障、传输线路中的脉冲干扰、图像量化误差等。例如，工业相机拍摄金属表面时，可能因反光或传感器异常产生此类噪声。

1.3 滤波与噪声消除的关系

滤波是消除图像噪声的核心技术，其本质是通过一定的数学运算，对图像像素进行局部处理，抑制噪声信号的同时尽可能保留有效信息。滤波过程可理解为：用一个固定大小的“窗口”（称为卷积核）在图像上从左至右、从上至下滑动，对窗口覆盖的像素区域进行计算，并用计算结果替换窗口中心像素的值，从而实现噪声的平滑消除。

1.4 滤波与模糊、锐化的关联

很多初学者会混淆滤波、模糊和锐化的概念，其实三者都属于卷积运算的应用，核心区别在于卷积核的设计：

• 滤波是广义概念，包括噪声抑制（低通滤波）和细节增强（高通滤波）两类；
• 低通滤波：允许图像中的低频信号（平缓变化的区域）通过，抑制高频信号（噪声、边缘），从而实现噪声消除和图像平滑，本质上是一种模糊操作；
• 高通滤波：与低通滤波相反，允许高频信号通过，增强图像边缘和细节，实现锐化效果，常用于噪声消除后的细节恢复。

二、滤波算法核心基础

2.1 卷积核与滑动窗口

卷积核（又称滤波器模板）是滤波算法的核心，是一个固定大小的矩阵（如3×3、5×5），矩阵中的每个元素称为权重值。滤波过程中，卷积核作为滑动窗口，其中心对准当前处理的像素，窗口覆盖的所有像素与对应权重值相乘后求和（或其他运算），结果即为中心像素的新值。

例如，3×3的卷积核在4×4的图像上滑动时，需要对图像边界进行填充（称为边界填充），确保卷积核能够完整覆盖边界像素。常用的边界填充方式包括BORDER_REFLECT_101（镜像填充）和BORDER_REPLICATE（复制填充），不同滤波算法的默认填充方式会在后续章节详细说明。

2.2 滤波算法的分类

根据运算方式的不同，常用的滤波算法可分为线性滤波和非线性滤波两大类，其核心区别在于是否对像素值进行线性组合运算：

• 线性滤波：对窗口内的像素值进行加权求和等线性运算，卷积核权重固定。优点是计算速度快，适合处理均匀分布的噪声；缺点是容易模糊图像边缘细节。常见类型包括均值滤波、方框滤波、高斯滤波。
• 非线性滤波：通过像素值的排序、统计等非线性运算得到结果，不依赖固定的卷积核权重。优点是能在消除噪声的同时保留边缘信息，适合处理脉冲类噪声；缺点是计算复杂度较高，运算速度相对较慢。常见类型包括中值滤波、双边滤波。

三、5种主流滤波算法详解

3.1 均值滤波（Mean Filter）

3.1.1 算法原理

均值滤波是最简单的线性滤波算法，其核心思想是“局部平均”：对于每个像素，用其周围邻域内所有像素值的平均值作为该像素的新值。以3×3卷积核为例，其权重矩阵如下：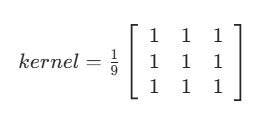

该矩阵表示，窗口内每个像素的权重相等（均为1/9），中心像素的新值等于窗口内9个像素值的总和除以9。

3.1.2 关键参数

在滤波算法组件中，均值滤波的参数配置非常简洁，仅需设置一个核心参数：

• ksize：卷积核的大小，常用值为3（3×3）、5（5×5）、7（7×7）等奇数。ksize越大，滤波效果越强（噪声消除越彻底），但图像模糊程度也会越严重，细节丢失越多。例如，ksize=3时，滤波后图像细节保留较好；ksize=7时，噪声消除更彻底，但边缘会明显模糊。

3.1.3 运算过程

以4×4图像为例，使用3×3卷积核进行均值滤波的具体步骤如下：

1. 对图像进行边界填充（默认使用BORDER_REFLECT_101镜像填充），确保卷积核能够覆盖图像四个角落的像素；
2. 将3×3卷积核的中心对准图像的第一个像素（非边界像素），计算窗口内9个像素值的总和；
3. 将总和除以9，得到的平均值作为中心像素的新值；
4. 卷积核从左至右、从上至下滑动，重复步骤2-3，直至遍历完整个图像，最终得到滤波后的4×4图像。

3.1.4 优缺点与适用场景

• 优点：算法简单易懂，计算量小，运算速度快，适合实时处理场景；对高斯噪声有一定的抑制效果。
• 缺点：对所有像素一视同仁地加权平均，会同时模糊噪声和图像边缘、细节，导致图像整体变得模糊，细节丢失严重。
• 适用场景：对图像清晰度要求不高，仅需快速消除轻微高斯噪声的场景，例如监控画面的实时降噪、低精度图像的预处理等。

3.2 方框滤波（Box Filter）

3.2.1 算法原理

方框滤波是均值滤波的扩展形式，核心思想与均值滤波类似，都是对窗口内的像素进行求和运算，但通过参数控制是否对求和结果进行归一化。其3×3卷积核的一般形式如下：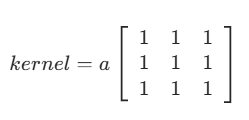

其中，a为归一化系数，其值由参数normalize决定，这是方框滤波与均值滤波的核心区别。

3.2.2 关键参数

方框滤波的参数相对丰富，包括3个核心参数，需根据实际需求灵活配置：

• ksize：卷积核大小，与均值滤波一致，常用3×3、5×5等奇数尺寸，决定了滤波窗口的范围。
• ddepth：输出图像的深度，即像素值的位数（如8位、16位），取值为-1时表示使用原图像的深度，无需额外转换，是最常用的配置。
• normalize：归一化开关，布尔值（True/False）：
  • 当normalize=True时，a=1/(ksize×ksize)，此时方框滤波等价于均值滤波，求和后除以窗口内像素总数，得到平均值；
  • 当normalize=False时，a=1，此时方框滤波直接计算窗口内像素值的总和，不进行归一化，适用于需要保留像素值总和特征的场景（如亮度检测）。

3.2.3 运算过程

方框滤波的运算流程与均值滤波基本一致，具体步骤如下：

1. 采用BORDER_REFLECT_101方式进行边界填充（与均值滤波默认填充方式相同）；
2. 卷积核在图像上滑动，覆盖当前像素的邻域区域；
3. 根据normalize参数选择运算方式：若归一化则计算加权平均（权重均为1/(ksize×ksize)），若不归一则计算像素值总和；
4. 将计算结果作为中心像素的新值，完成整个图像的遍历。

3.2.4 优缺点与适用场景

• 优点：灵活性高，可通过normalize参数切换“均值计算”和“总和计算”两种模式；运算速度与均值滤波相当，适合批量处理。
• 缺点：同样属于线性滤波，会模糊图像边缘和细节；当normalize=False时，可能因像素值总和过大导致图像过亮（像素值溢出）。
• 适用场景：
  • normalize=True时，与均值滤波适用场景一致，可用于轻微高斯噪声的快速消除；
  • normalize=False时，适用于需要保留区域亮度总和的场景，如工业图像中的光斑检测、目标面积计算等。

3.3 高斯滤波（Gaussian Filter）

3.3.1 算法原理

高斯滤波是应用最广泛的线性滤波算法，其核心改进在于卷积核的权重分布：不再采用均值滤波和方框滤波的均匀权重，而是基于高斯函数设计权重矩阵，使窗口中心像素的权重最大，越远离中心的像素权重越小，呈正态分布。

这种权重分布的优势在于：在抑制噪声的同时，能更好地保留图像的细节信息，因为中心像素（有效信息的核心）在计算中占据主导地位。3×3高斯滤波的标准卷积核如下：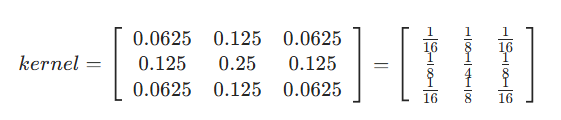

卷积核的权重值通过高斯函数计算得到。高斯函数的二维形式为：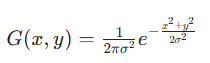

其中，(x,y)是卷积核中像素相对于中心的坐标（中心像素坐标为(0,0)），σ（sigma）是高斯分布的标准差，决定了权重的衰减速度。

3.3.2 关键参数

高斯滤波的参数配置直接影响滤波效果，核心参数包括2个：

• ksize：卷积核大小，常用3×3、5×5、7×7等奇数。需要注意的是，当ksize大于7且未手动设置σ时，系统会通过固定公式自动计算σ值（通常为ksize/6），确保权重分布合理。
• sigmaX：高斯分布在x方向的标准差（由于图像是二维的，通常默认x和y方向的标准差相同，即sigmaY=sigmaX）。sigmaX的值越大，权重衰减越慢，卷积核的影响范围越广，图像模糊效果越明显；sigmaX越小，权重越集中在中心，细节保留越好，但噪声抑制效果会减弱。

3.3.3 运算过程

高斯滤波的运算流程与前两种线性滤波类似，但增加了卷积核权重的计算步骤：

1. 根据ksize和sigmaX参数，通过高斯函数生成对应的权重矩阵（卷积核）；
2. 对图像进行BORDER_REFLECT_101边界填充；
3. 卷积核在图像上滑动，将窗口内每个像素值与对应权重相乘后求和；
4. 求和结果作为中心像素的新值，完成整个图像的滤波处理。

3.3.4 优缺点与适用场景

• 优点：噪声抑制效果好，尤其对高斯噪声的消除能力突出；权重分布合理，相比均值滤波和方框滤波，能更好地保留图像细节，是兼顾降噪和细节保留的平衡选择；
• 缺点：卷积核权重计算复杂，运算速度比均值滤波和方框滤波慢；对椒盐噪声的抑制效果有限。
• 适用场景：高斯噪声为主的图像降噪，如低光环境下的照片处理、工业相机采集的产品图像预处理、医学影像（如X光片、CT图像）的噪声消除等。由于其优秀的综合性能，高斯滤波被称为“最有用的滤波器”，在不确定噪声类型时，可作为首选的降噪算法。

3.4 中值滤波（Median Filter）

3.4.1 算法原理

中值滤波是一种经典的非线性滤波算法，与线性滤波的核心区别在于：不进行像素值的加权求和，而是对窗口内的像素值进行排序后，取中间值作为中心像素的新值。

例如，使用3×3窗口处理某区域像素时，先将窗口内的9个像素值按从小到大排序，取第5个值（中位数）替换中心像素的原始值。这种非线性运算的优势在于：能有效剔除异常值（如椒盐噪声的黑白斑点），同时保留边缘细节，因为异常值在排序后会处于序列的两端，不会影响中间值的选择。

3.4.2 关键参数

中值滤波的参数相对简单，仅需配置1个核心参数：

• ksize：卷积核（窗口）大小，常用3×3、5×5等奇数。与线性滤波不同，中值滤波的ksize对效果影响显著：ksize越小，细节保留越好，但噪声抑制能力较弱；ksize越大，噪声消除越彻底，但可能导致图像边缘出现“块状”失真。

需要注意的是，中值滤波的边界填充方式与其他线性滤波不同，默认采用BORDER_REPLICATE（复制填充），即复制图像边界的像素值来填充窗口，确保边界处理的一致性。

3.4.3 运算过程

中值滤波的运算流程与线性滤波差异较大，具体步骤如下：

1. 采用BORDER_REPLICATE方式进行边界填充；
2. 卷积核在图像上滑动，覆盖当前像素的邻域区域；
3. 提取窗口内所有像素的数值，进行升序（或降序）排序；
4. 选取排序后的中间值（若窗口内像素数为偶数，则取中间两个值的平均或任意一个中间值），作为中心像素的新值；
5. 重复上述步骤，直至遍历完整个图像。

3.4.4 优缺点与适用场景

• 优点：对椒盐噪声和斑点噪声的抑制效果极佳，是处理这类噪声的首选算法；非线性运算不会模糊图像边缘，能有效保留细节信息；算法逻辑简单，易于实现。
• 缺点：运算速度比线性滤波慢，因为需要进行排序操作，尤其当ksize较大时，计算量显著增加；对高斯噪声的抑制效果不如高斯滤波。
• 适用场景：椒盐噪声、斑点噪声为主的图像降噪，如工业监控图像、印刷品扫描图像、遥感图像等。例如，处理因传感器故障导致的黑白斑点图像，中值滤波能在剔除噪声的同时，保持目标物体的边缘清晰。

3.5 双边滤波（Bilateral Filter）

3.5.1 算法原理

前面介绍的线性滤波（均值、方框、高斯）都存在一个共同的问题：在消除噪声的同时，会模糊图像的边缘细节，因为它们仅考虑了像素的空间位置（空域信息），而忽略了像素值的差异（值域信息）。双边滤波的核心创新的是：同时考虑空域信息和值域信息，在抑制噪声的同时，最大限度地保留边缘细节。

双边滤波的原理是结合两个高斯滤波器：

1. 空域高斯滤波器：与普通高斯滤波一致，基于像素的空间距离计算权重，距离中心越近的像素权重越大；
2. 值域高斯滤波器：基于像素值的相似度计算权重，像素值与中心像素越接近，权重越大。

最终的权重的是空域权重和值域权重的乘积，公式如下：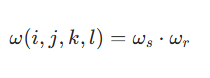

其中，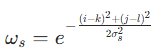
（空域权重，(i,j)为中心像素坐标，(k,l)为邻域像素坐标），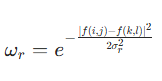

（值域权重，f(i,j)为中心像素值，f(k,l)为邻域像素值）。

通过这种双重权重计算，双边滤波在处理边缘区域时，由于边缘两侧的像素值差异较大，值域权重会显著降低，从而避免边缘被模糊；而在平坦区域，像素值差异小，值域权重接近1，滤波效果与高斯滤波类似，能有效抑制噪声。

3.5.2 关键参数

双边滤波的参数较多，需要根据图像特点和需求灵活调整，核心参数包括4个：

• ksize：卷积核大小，常用3×3、5×5、9×9等奇数。ksize越大，滤波范围越广，但运算速度越慢。
• d：邻域直径，即每个像素的邻域范围大小。d值越大，参与计算的邻域像素越多，降噪效果越强，但运算效率越低。实际应用中，实时场景建议d=5，离线处理严重噪声时可设d=9。
• sigmaColor：颜色空间的标准差，决定了像素值相似度的权重衰减速度。sigmaColor越大，允许更多像素值差异较大的像素参与滤波（即“颜色混合范围更广”）；sigmaColor越小，仅允许像素值接近的像素参与计算，边缘保留效果更明显。
• sigmaSpace：坐标空间的标准差，与高斯滤波的sigmaX作用类似，决定了空间距离的权重衰减速度。sigmaSpace越大，空间距离较远的像素也会对中心像素产生影响；sigmaSpace越小，权重越集中在中心像素附近。

关于参数配置的经验法则：

1. 通常将sigmaColor和sigmaSpace设置为相等的值，简化调整过程；
2. 当sigmaColor和sigmaSpace小于10时，滤波效果微弱；大于150时，滤波效果过强，图像会呈现“卡通化”效果；
3. 避免设置过大的d值（d>5），否则会导致运算速度急剧下降，影响实时性。

3.5.3 运算过程

双边滤波的运算流程相对复杂，具体步骤如下：

1. 采用BORDER_REFLECT_101方式进行边界填充；
2. 卷积核在图像上滑动，确定中心像素(i,j)及其邻域像素(k,l)；
3. 计算每个邻域像素的空域权重ωs（基于空间距离）和值域权重ωr（基于像素值差异）；
4. 计算最终权重ω=ωs×ωr，并对所有邻域像素的权重进行归一化（权重总和为1）；
5. 邻域像素值与对应归一化权重相乘后求和，结果作为中心像素的新值；
6. 重复上述步骤，完成整个图像的滤波处理。

3.5.4 优缺点与适用场景

• 优点：能在抑制噪声的同时，最大限度地保留图像边缘细节，解决了线性滤波“降噪必模糊边缘”的痛点；对高斯噪声和轻微椒盐噪声都有较好的抑制效果。
• 缺点：计算复杂度高，运算速度是所有滤波算法中最慢的；参数调整复杂，需要多次实验才能达到最佳效果。
• 适用场景：对边缘细节要求高的图像降噪，如人脸识别中的面部图像预处理、文物修复中的图像去噪、工业检测中的产品边缘保留、航拍图像的细节增强等。

四、5种滤波算法对比分析

4.1 核心特性对比

为了方便大家快速选择合适的滤波算法，下面从滤波类型、核心思想、权重特点、边缘保留、运算速度等维度进行综合对比：

算法类型	滤波类型	核心思想	权重特点	边缘保留效果	运算速度
均值滤波	线性	邻域像素平均值	均匀权重	差（模糊边缘）	最快
方框滤波	线性	邻域像素求和（可归一化）	均匀权重（可切换归一化）	差（模糊边缘）	快
高斯滤波	线性	邻域像素加权平均（高斯权重）	中心权重最大，边缘权重递减	一般（轻微模糊）	中等
中值滤波	非线性	邻域像素排序取中值	无固定权重（依赖排序）	好（保留边缘）	较慢
双边滤波	非线性	空域+值域双重权重加权平均	动态权重（随像素位置和值变化）	最好（精准保留）	最慢

4.2 噪声适配性对比

不同滤波算法对高斯噪声和椒盐噪声的抑制效果差异显著，具体适配性如下：

算法类型	高斯噪声抑制效果	椒盐噪声抑制效果	最佳适配噪声类型
均值滤波	一般	差	轻微高斯噪声
方框滤波	一般	差	轻微高斯噪声
高斯滤波	好	一般	高斯噪声
中值滤波	一般	好	椒盐噪声、斑点噪声
双边滤波	好	一般	高斯噪声（需保留边缘）

4.3 实用选择策略

根据实际应用场景，可按照以下策略快速选择滤波算法：

1. 若不确定噪声类型，优先选择高斯滤波（综合性能最优），其次是均值滤波（快速降噪）；
2. 若明确是椒盐噪声或斑点噪声，直接选择中值滤波（针对性最强）；
3. 若需要在降噪的同时保留边缘细节（如目标检测、特征提取前的预处理），选择双边滤波；
4. 若追求运算速度（如实时监控、批量处理），选择均值滤波或方框滤波（normalize=True）；
5. 若需要计算区域像素总和（如亮度分析、面积检测），选择方框滤波（normalize=False）。

五、图像噪点消除实验操作指南

5.1 实验结果分析

5.1.1 不同算法处理效果对比

以含高斯噪声和椒盐噪声的图像为例，不同滤波算法的处理效果如下：

• 均值滤波：噪声有所抑制，但图像整体模糊，边缘细节丢失；
• 方框滤波（normalize=True）：效果与均值滤波类似，噪声抑制和模糊程度基本一致；
• 高斯滤波：高斯噪声抑制效果明显，图像模糊程度低于均值滤波，细节保留更好；
• 中值滤波：椒盐噪声的黑白斑点完全消失，边缘细节清晰，但图像整体略有“块状”感；
• 双边滤波：高斯噪声得到有效抑制，图像边缘细节几乎完全保留，整体清晰度最高。

5.1.2 参数调整对效果的影响

以高斯滤波为例，不同参数配置的效果差异：

• ksize=3，sigmaX=0.5：噪声抑制效果较弱，但细节保留最好；
• ksize=5，sigmaX=1.5：噪声抑制和细节保留达到平衡，适合大多数场景；
• ksize=7，sigmaX=3.0：噪声抑制效果最强，但图像模糊程度明显增加，细节丢失较多。

以双边滤波为例，sigmaColor和sigmaSpace的影响：

• sigmaColor=30，sigmaSpace=30：边缘保留效果好，但噪声抑制不足；
• sigmaColor=50，sigmaSpace=50：噪声抑制和边缘保留平衡；
• sigmaColor=100，sigmaSpace=100：噪声抑制效果强，但图像出现轻微“卡通化”。

六、Python代码实现与实战案例

本节将基于OpenCV库，实现5种滤波算法的Python代码，并提供完整的实战案例，包括图像读取、滤波处理、结果显示和保存，方便大家直接运行和修改。

6.1 环境准备

首先确保已安装OpenCV库，若未安装，可通过以下命令安装：

pip install opencv-python

6.2 完整代码实现

以下代码实现了均值滤波、方框滤波、高斯滤波、中值滤波、双边滤波的完整流程，包含参数配置、效果对比和结果保存：

import cv2
import numpy as np
import matplotlib.pyplot as plt  # 用于合并显示多子图


def load_image(image_path):
    """读取图像，返回BGR格式的图像数组（OpenCV默认）"""
    image = cv2.imread('lena.png')
    if image is None:
        raise ValueError("无法读取图像，请检查路径是否正确或图像格式是否支持（优先png/jpg）")
    return image


def mean_filter(image, ksize=3):
    """均值滤波：邻域像素取平均，简单快速但易模糊细节"""
    return cv2.blur(image, (ksize, ksize))


def box_filter(image, ksize=3, ddepth=-1, normalize=True):
    """方框滤波：可切换归一化（等价均值滤波）/非归一化（像素求和）"""
    return cv2.boxFilter(image, ddepth, (ksize, ksize), normalize=normalize)


def gaussian_filter(image, ksize=3, sigmaX=1.5):
    """高斯滤波：中心像素权重高，兼顾降噪与细节保留，适合高斯噪声"""
    return cv2.GaussianBlur(image, (ksize, ksize), sigmaX)


def median_filter(image, ksize=3):
    """中值滤波：邻域像素排序取中值，擅长消除椒盐噪声，无边缘模糊"""
    return cv2.medianBlur(image, ksize)


def bilateral_filter(image, d=5, sigmaColor=50, sigmaSpace=50):
    """双边滤波：结合空域+值域权重，降噪同时精准保留边缘细节"""
    return cv2.bilateralFilter(image, d, sigmaColor, sigmaSpace)


def merge_and_show_results(original, mean_img, box_img, gaussian_img, median_img, bilateral_img,
                           save_path="./results/"):
    """
    合并显示所有结果（单图多子图）+ 保存单张结果图
    参数：
        original: 原始图像（BGR格式）
        mean_img~bilateral_img: 5种滤波结果（BGR格式）
        save_path: 结果保存目录
    """
    # 1. 预处理：创建目录 + BGR转RGB（matplotlib默认RGB显示）
    import os
    if not os.path.exists(save_path):
        os.makedirs(save_path)  # 不存在则创建结果目录

    # OpenCV读取的是BGR格式，matplotlib需转为RGB格式才能正常显示颜色
    def bgr2rgb(img):
        return cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

    # 转换所有图像格式
    original_rgb = bgr2rgb(original)
    mean_rgb = bgr2rgb(mean_img)
    box_rgb = bgr2rgb(box_img)
    gaussian_rgb = bgr2rgb(gaussian_img)
    median_rgb = bgr2rgb(median_img)
    bilateral_rgb = bgr2rgb(bilateral_img)

    # 2. 合并显示：2行3列布局（共6个子图）
    plt.figure(figsize=(18, 12))  # 设置整体图大小（宽18英寸，高12英寸），可根据屏幕调整
    plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'SimHei']  # 支持英文/中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示异常

    # 子图1：原始图像
    plt.subplot(2, 3, 1)  # 第2行、第3列、第1个子图
    plt.imshow(original_rgb)
    plt.title("Original Image\n（原始图像）", fontsize=14, fontweight='bold')
    plt.axis('off')  # 隐藏坐标轴，避免干扰视觉

    # 子图2：均值滤波
    plt.subplot(2, 3, 2)
    plt.imshow(mean_rgb)
    plt.title("Mean Filter\n（均值滤波：简单快速，细节模糊）", fontsize=14, fontweight='bold')
    plt.axis('off')

    # 子图3：方框滤波（归一化=均值滤波）
    plt.subplot(2, 3, 3)
    plt.imshow(box_rgb)
    plt.title("Box Filter (Normalized)\n（方框滤波：等价均值，可切换求和模式）", fontsize=14, fontweight='bold')
    plt.axis('off')

    # 子图4：高斯滤波
    plt.subplot(2, 3, 4)
    plt.imshow(gaussian_rgb)
    plt.title("Gaussian Filter\n（高斯滤波：高斯噪声优选，细节保留好）", fontsize=14, fontweight='bold')
    plt.axis('off')

    # 子图5：中值滤波
    plt.subplot(2, 3, 5)
    plt.imshow(median_rgb)
    plt.title("Median Filter\n（中值滤波：椒盐噪声克星，无边缘模糊）", fontsize=14, fontweight='bold')
    plt.axis('off')

    # 子图6：双边滤波
    plt.subplot(2, 3, 6)
    plt.imshow(bilateral_rgb)
    plt.title("Bilateral Filter\n（双边滤波：降噪+边缘保留，效果最佳）", fontsize=14, fontweight='bold')
    plt.axis('off')

    # 调整子图间距，避免标签重叠
    plt.tight_layout(pad=3.0)  # pad=3.0：子图间间距（英寸），可按需调整

    # 3. 保存结果：同时保存“合并图”和“单张结果图”
    # 保存合并图（高清，dpi=300）
    merge_save_path = os.path.join(save_path, "all_filters_comparison.png")
    plt.savefig(merge_save_path, dpi=300, bbox_inches='tight')  # bbox_inches='tight'：去除多余空白
    print(f"合并对比图已保存至：{merge_save_path}")

    # 保存单张结果图（保持原始分辨率）
    single_saves = [
        (original, "original.jpg", "原始图像"),
        (mean_img, "mean_filter.jpg", "均值滤波结果"),
        (box_img, "box_filter.jpg", "方框滤波结果"),
        (gaussian_img, "gaussian_filter.jpg", "高斯滤波结果"),
        (median_img, "median_filter.jpg", "中值滤波结果"),
        (bilateral_img, "bilateral_filter.jpg", "双边滤波结果")
    ]
    for img, filename, desc in single_saves:
        save_path_single = os.path.join(save_path, filename)
        cv2.imwrite(save_path_single, img)
        print(f"{desc}已保存至：{save_path_single}")

    # 显示合并图（弹窗形式，关闭弹窗后程序继续）
    plt.show()


if __name__ == "__main__":
    # -------------------------- 配置参数（可按需修改） --------------------------
    image_path = "./demo.png"  # 测试图像路径（请确保该路径下有demo.png文件）
    ksize = 3  # 卷积核大小（建议奇数：3/5/7，越大降噪越强但模糊越明显）
    sigmaX = 1.5  # 高斯滤波标准差（越大模糊越强，1.0~2.0为常用范围）
    d = 5  # 双边滤波邻域直径（实时场景建议5，离线高噪声场景可设9）
    sigmaColor = 50  # 双边滤波颜色相似度权重（50~100，越大颜色混合范围越广）
    sigmaSpace = 50  # 双边滤波空间距离权重（50~100，越大空间影响范围越广）
    save_root = "./filter_results/"  # 结果保存根目录（自动创建）
    # ---------------------------------------------------------------------------

    # 1. 读取原始图像
    try:
        original_image = load_image(image_path)
        print(f"成功读取原始图像，分辨率：{original_image.shape[1]}x{original_image.shape[0]}（宽x高）")
    except ValueError as e:
        print(f"图像读取失败：{e}")
        exit()  # 读取失败则退出程序

    # 2. 执行5种滤波算法
    mean_result = mean_filter(original_image, ksize=ksize)
    box_result = box_filter(original_image, ksize=ksize, normalize=True)  # 归一化=均值滤波
    gaussian_result = gaussian_filter(original_image, ksize=ksize, sigmaX=sigmaX)
    median_result = median_filter(original_image, ksize=ksize)
    bilateral_result = bilateral_filter(original_image, d=d, sigmaColor=sigmaColor, sigmaSpace=sigmaSpace)
    print("所有滤波算法执行完成，开始合并显示与保存...")

    # 3. 合并显示+保存结果
    merge_and_show_results(
        original=original_image,
        mean_img=mean_result,
        box_img=box_result,
        gaussian_img=gaussian_result,
        median_img=median_result,
        bilateral_img=bilateral_result,
        save_path=save_root
    )
    print("所有操作完成！")

输出结果为

6.3 代码说明与使用指南

6.3.1 核心函数功能

• load_image：读取图像文件，支持主流格式（png、jpg、jpeg等），并进行路径有效性检查；

• show_and_save_results：统一显示所有滤波结果，并将结果保存到指定目录，支持图像大小调整（避免因图像过大无法完整显示）。

七、总结与拓展

本文全面覆盖了图像噪点消除的核心技术，从基础概念到实战应用，关键要点如下：

1. 图像噪声主要分为高斯噪声和椒盐噪声，其产生原因和视觉特征不同，需针对性选择滤波算法；
2. 线性滤波（均值、方框、高斯）运算速度快，适合高斯噪声，但会模糊边缘；非线性滤波（中值、双边）能保留边缘，中值滤波对椒盐噪声最优，双边滤波综合性能最佳；
3. 参数配置是影响滤波效果的关键，如高斯滤波的sigmaX、双边滤波的sigmaColor和sigmaSpace，需根据图像特点灵活调整；