【大模型后训练专题】LoRA原理及实现

摘要本文深入解析LoRA（Low-Rank Adaptation）技术原理及工程实现。LoRA通过冻结预训练模型参数，仅训练低秩增量矩阵ΔW=BA（B∈ℝ^{d×r}, A∈ℝ^{r×d}），显著降低微调参数量。核心观点包括：低秩合理性：预训练模型已具备通用能力，下游任务只需低维调整；超参数设置：rank(r)控制子空间维度，alpha实现方差归一化，建议r=4/8/16，alpha=r~2

不知名rapper

1303人浏览 · 2025-11-27 17:34:21

不知名rapper · 2025-11-27 17:34:21 发布

在这里插入图片描述

🧔 这里是九年义务漏网鲨鱼，研究生在读，主要研究方向是人脸伪造检测,长期致力于研究多模态大模型技术；国家奖学金获得者，国家级大创项目一项，发明专利一篇，多篇论文在投，蓝桥杯国家级奖项、妈妈杯一等奖。
✍ 博客主要内容为大模型技术的学习以及相关面经，本人已得到B站、百度、唯品会等多段多模态大模型的实习offer，为了能够紧跟前沿知识，决定写一个“从零学习 RL”主题的专栏。这个专栏将记录我个人的主观学习过程，因此会存在错误，若有出错，欢迎大家在评论区帮助我指出。除此之外，博客内容也会分享一些我在本科期间的一些知识以及项目经验。
🌎 Github仓库地址：Baby Awesome Reinforcement Learning for LLMs and Agentic AI
📩 有兴趣合作的研究者可以联系我：yirongzzz@163.com

LoRA 原理及实现

文章目录

LoRA 原理及实现

前言

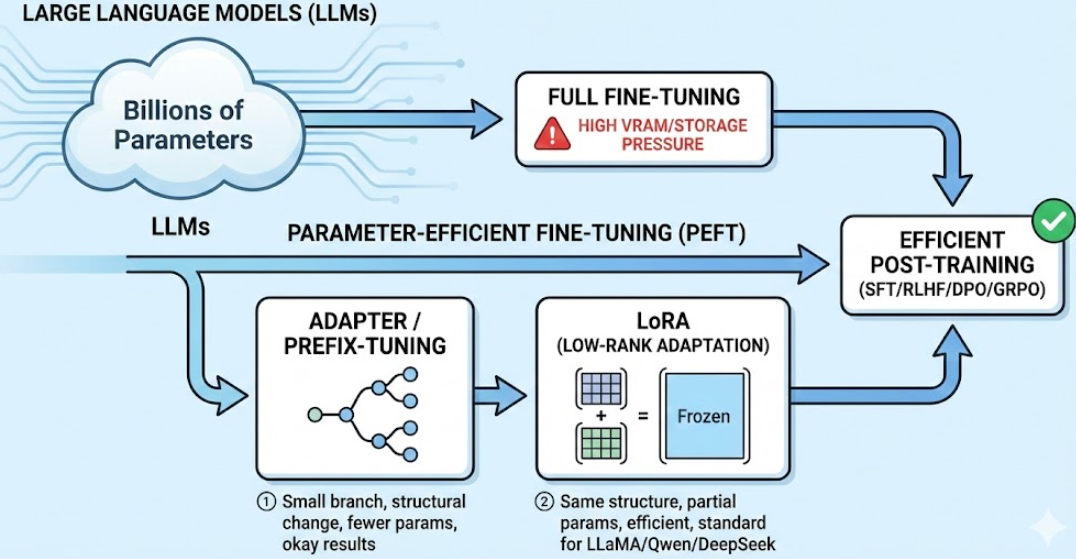
✍ 在大模型后训练这条线里，大模型的参数量往往是几十亿、上百亿。SFT / RLHF / DPO / GRPO 这些“训练流程”本身固然重要，但如果用 全参数微调（Full Fine-tuning） 去做，显存和存储压力会非常大：为了能够减少训练参数，工业界和开源社区自然发展出了各种 Parameter-Efficient Fine-Tuning（PEFT）方法，里面最经典的两条线就是：

LoRA（Low-Rank Adaptation） ——几乎成了 LLaMA / Qwen / DeepSeek 等各种开源 LLM 的微调标配。

Adapter / Prefix-tuning ——参数少，效果一般，改动结构大；

直观上理解就是： ① Adapter训练了一个小分支 ② LoRA保持架构不变，训练了一部分参数

本章节重点讲解LoRA的原理及代码实现。

在这里插入图片描述

一、LoRA 入门

全参数微调相对于把预训练模型所有参数都当成可学习参数，直接在下游任务上继续训练。而在前言我们也提到过，LoRA的核心想法：不需要所有的参数同时训练，冻结原始参数，只训练一个小的 ΔW。

🧠 Q1：为什么可以直接通过一个低秩矩阵训练就可以达到好的效果？

1）预训练模型已经学到大部分通用能力，下游只需要“小幅度方向修正”，本身就低维；

2）实证上，全参微调的权重差分 ΔW 做 SVD 会发现谱衰减很快，“有效秩”不高；

3）LoRA 把更新限制在低秩子空间里，相当于一种强正则，在有限数据下往往更不容易过拟合。

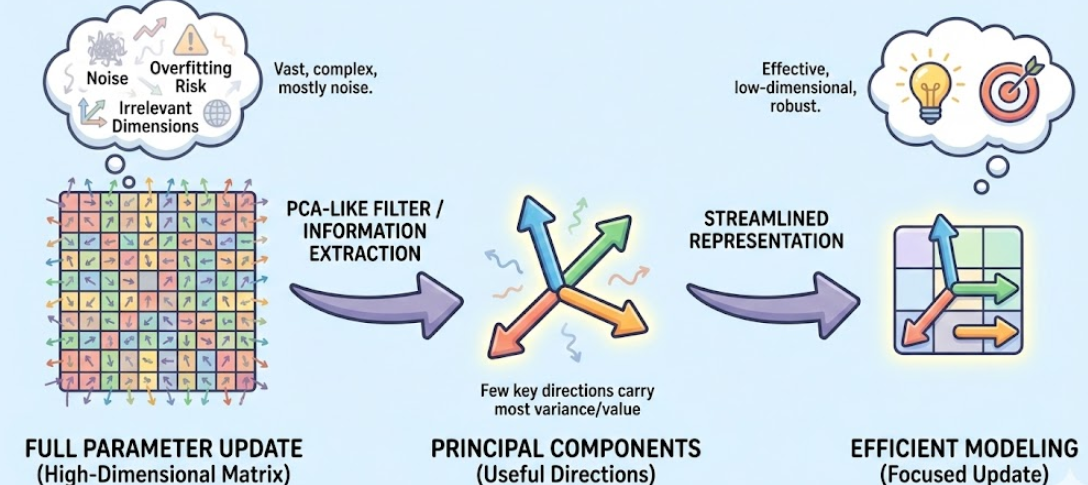
💡 更直观地类比，可以把全参数更新看成一个高维矩阵，而真正“有用”的信息只集中在少数几个方向上，就像 PCA 里只有前几维主成分承载了大部分方差；其余大量维度对应的只是很小的奇异值或噪声成分，对任务几乎没有贡献，甚至会带来过拟合。

在这里插入图片描述

了解了为什么可以这么做后，我们来看一下LoRA在实际工程中是怎么实现的, 以 Transformer 里最常见的线性层为例：

原始权重矩阵： $W_0 \in \mathbb{R}^{d_{\text{out}} \times d_{\text{in}}}$
原来的前向传递： $h_{\text{out}} = W_0 x$

全参数微调会直接更新 $W_0$ 。而 LoRA 的做法是：冻结 $W_0$ ，只学习一个“增量”矩阵 $\Delta W$ ，让： $W_0 + \Delta W$

LoRA 进一步假设： $\Delta W$ 是 低秩矩阵，也就是：

$\Delta W = B A,\quad B\in\mathbb{R}^{d_{\text{out}}\times r},\ A\in\mathbb{R}^{r\times d_{\text{in}}},\ r \ll \min(d_{\text{out}}, d_{\text{in}})$

于是前向变成：

$h_{\text{out}} = W_0 x + BAx$

$W_0$ ：冻结，不训练；
$A, B$ ：是 LoRA 的参数，训练时可学习。

💡 因此，训练LoRA过程中仅仅需要学习极少的增量参数，实现接近全参微调的效果，并保持部署方式几乎不变

🧠 Q2：“为什么叫 Low-Rank？这个 low-rank 假设合理吗？”

把 $\Delta W$ 写成 $B A$ 的形式，其 rank 至多为 $r$ ，因此是一个 低秩矩阵；
直觉上，相比重新学习一个大矩阵，我们只用一个“小瓶颈层”去表达任务特定的偏移；
实证上许多 NLP 任务显示：任务相关的更新矩阵在某种意义上是低秩的，也就是 “只需要少量方向上的调整”。

二、LoRA 的工程实战

上面一节更多是在讲 “LoRA 是什么 / 数学上在干嘛”，事实上，在理论方面LoRA并没有太多深入，可以理解为一个主成分在微调上的应用。在面试过程中，面试官更在意的是你是如何设置你的超参数的、挂在哪些层等等。

先来看看有哪些超参数：

r：低秩 rank，决定 更新子空间的维度，越大表达力越强，参数也越多；(相对于主成分的数量)
alpha：缩放因子，等价于对 $\Delta W$ 做一个整体 scale；
lora_dropout：只作用在 LoRA 分支上的 dropout；
target_modules：在哪些 Linear 层上加 LoRA（Q/K/V/O 还是 FFN）。

2.1 缩放因子

🧠 Q3：为什么需要缩放因子

在论文中通常会引入一个 scaling 因子 $\alpha$ ，定义成： $\Delta W = \frac{\alpha}{r} BA$

如果我们不除以 $r$ ，当你把 rank 从 4 提到 32 时， $B A$ 的方差会随着 $r$ 增大，初始的 LoRA 更新 $\Delta W$ 可能一下子比原始 $W_0$ 大很多；

这样一来，一开始训练几步里，模型行为会被 LoRA 分支“拉得很偏”，破坏预训练好的表示；

用 $\frac{\alpha}{r}$ 做一个归一化，可以让 “不同 r 下 LoRA 的初始扰动处于同一量级”，避免 rank 一变、训练稳定性就完全变样。

因此，目的是为了做一个方差归一化，让不同 $r$ 下 LoRA 的初始影响保持可控，防止 $r$ 比较大， $B A$ 的方差会随 $r$ 增大；

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

💡 常见经验配置：

r = 4 / 8 / 16
alpha = r 或 alpha = 2 * r

🧠 Q4：你是如何选择r和alpha的

① 默认选 r=8, alpha=8~16，基本不会太离谱。如果任务比较简单（小数据、风格单一），可以从 r = 4 起步，防止一上来容量太大过拟合。

② 根据任务和模型规模动态调整，可以适当 增大 r（比如 16）或扩大 LoRA 覆盖层数；

③ 从训练曲线和效果回看参数是否合适，如果训练 loss 很快降到很低，但验证集表现一般，可以尝试减小 r 或提高 lora_dropout；如果 loss 长期降不下去，模型几乎学不动：可能是 r 太小、LoRA 覆盖层太少，表达力不够； → 先考虑增加 r 或多加几层 LoRA，而不是先动学习率。

2.2 LoRA Dropout

在很多工程实现中，LoRA 会在 $A x$ 后加一个 dropout，例如： $h_{\text{out}} = W_0 x + \frac{\alpha}{r} B(\text{Dropout}(Ax))$

典型场景：

只用几万条 SFT 数据；
或者风格非常集中的小领域（比如某个 IP 角色扮演）。

这时 LoRA 很容易把小数据“记死”，泛化变差。也就是我们刚刚说的，如果训练 loss 很快降到很低，但验证集表现一般，这时，可以尝试在 LoRA 分支上单独加一个 lora_dropout，常见设置：

0.05 ~ 0.1：对应 LoRA path 上的轻微随机屏蔽；

🧠 Q5：为什么 Dropout 只加在 LoRA 分支，不加在原始 Linear 上？

原始 $W_0$ 是预训练好的，不希望再破坏它；

LoRA 分支才是“任务特化偏移”，对它做一点随机正则，更安全；

对原始路径加 dropout 反而可能影响已有能力，属于“动手术动到心脏上了”。

2.3 给哪些层加 LoRA

这也是面试官更喜欢问的问题之一，也是我们在实战中更关心的问题，如何加，加在哪里？LLM 里最常见的做法是：只给 Attention 加 LoRA，尤其是：

Self-Attention 里的 Q / K / V / O projection；
或者只在 Q / V 上加 LoRA（常见“轻量实践方案”）。

原因很直观：

注意力层直接决定“信息流怎么路由”，对模型行为影响最大；
FFN（MLP）层更多是“非线性变换”，某些任务上边际收益会略逊于 Attention；
在 GPU 资源有限的情况下，优先把 LoRA 参数预算砸在 Q/V 上，性价比高。

🧠 Q6：在 LLaMA / Qwen 这类 LLM 上做 LoRA，你会加在哪些权重矩阵上？

最常见做法是在 Self-Attention 的 Q、K、V、O 投影矩阵 上加 LoRA；

许多实践发现，只在 Q / V 上加 LoRA 就能取得不错效果，是一种很好的轻量配置；

给 FFN 的 Linear 加 LoRA 也可以，但在算力有限的情况下，我更倾向先把预算给 Attention，再视任务表现决定是否扩展到 FFN。

代码手撕

import torch
import torch.nn as nn
import math

class LoRALinear(nn.Module):
    def __init__(self, in_features, out_features, r=8, alpha=16, dropout=0.0, bias=True):
        super().__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.r = r
        self.scaling = alpha / r

        # 冻结的原始权重（可以从预训练模型里拷）
        self.weight = nn.Parameter(torch.empty(out_features, in_features))
        if bias:
            self.bias = nn.Parameter(torch.zeros(out_features))
        else:
            self.bias = None

        # LoRA 低秩分支
        if r > 0:
            self.lora_A = nn.Linear(in_features, r, bias=False)
            self.lora_B = nn.Linear(r, out_features, bias=False)
            self.lora_dropout = nn.Dropout(dropout)

            # 初始化：A 小随机，B 初始化为 0，让初始等价于原模型
            nn.init.kaiming_uniform_(self.lora_A.weight, a=math.sqrt(5))
            nn.init.zeros_(self.lora_B.weight)
        else:
            self.lora_A = None
            self.lora_B = None
            self.lora_dropout = None

    def forward(self, x):
        # 原始线性层
        result = x @ self.weight.T
        if self.bias is not None:
            result = result + self.bias

        # LoRA 分支
        if self.r > 0:
            lora_out = self.lora_B(self.lora_dropout(self.lora_A(x)))
            result = result + self.scaling * lora_out

        return result

peft 库实现

from transformers import AutoModelForCausalLM, AutoTokenizer
from peft import LoraConfig, get_peft_model

model_name = "Qwen/Qwen2-7B"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
    model_name,
    device_map="auto",
    torch_dtype="auto"
)

# 1. 定义 LoRA 配置
lora_config = LoraConfig(
    r=8,
    lora_alpha=16,
    lora_dropout=0.05,
    bias="none",
    task_type="CAUSAL_LM",
    target_modules=["q_proj", "v_proj"],  # 视模型结构调整
)

# 2. 注入 LoRA
model = get_peft_model(model, lora_config)
model.print_trainable_parameters()  # 看一下可训练参数比例

三、LoRA 家族扩展：QLoRA / DoRA / LoRA+

3.1 QLoRA：LoRA + 低比特量化

QLoRA 在此基础上再加一层：把 base 模型权重量化到 4bit，只在 LoRA 权重上保持高精度；

这样在不明显掉点的前提下，极大降低微调显存开销。

3.2 DoRA / LoRA+：更细致地控制方向与幅度 / 优化更新

DoRA（Weight-Decomposed Low-Rank Adaptation）：

把权重拆分为 “方向 × 幅度”，只在某个部分做低秩更新；直觉是更细粒度地控制“往哪儿改”而不是纯粹加一个矩阵。

LoRA+ / AdaLoRA 等：

在训练中动态调整 rank；或在不同层使用不同的 rank / scaling。

四、从零实现一个 LoRA Linear

import torch
import torch.nn as nn
import torch.nn.functional as F

class LoRALinear(nn.Module):
    def __init__(
        self,
        in_features,
        out_features,
        r=8,
        lora_alpha=8,
        lora_dropout=0.0,
        bias=True,
        fan_in_fan_out=False,  # 某些库里权重是反过来的
    ):
        super().__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.r = r
        self.lora_alpha = lora_alpha
        self.fan_in_fan_out = fan_in_fan_out

        # 原始权重（冻结部分）
        self.weight = nn.Parameter(torch.empty(out_features, in_features))
        if bias:
            self.bias = nn.Parameter(torch.zeros(out_features))
        else:
            self.bias = None

        # LoRA 权重（可训练部分）
        if r > 0:
            # A: [r, in_features]
            self.lora_A = nn.Parameter(torch.zeros(r, in_features))
            # B: [out_features, r]
            self.lora_B = nn.Parameter(torch.zeros(out_features, r))
            # scaling
            self.scaling = self.lora_alpha / self.r
            self.lora_dropout = nn.Dropout(p=lora_dropout)
        else:
            self.register_parameter("lora_A", None)
            self.register_parameter("lora_B", None)
            self.lora_dropout = nn.Identity()
            self.scaling = 1.0

        self.reset_parameters()

        # 训练时只训练 LoRA 权重
        self.weight.requires_grad = False

        self.merged = False  # 是否已经 merge 了 LoRA

    def reset_parameters(self):
        # 原始权重用 Kaiming 初始化
        nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
        if self.bias is not None:
            nn.init.zeros_(self.bias)
        # LoRA 部分建议用较小初始化：B = 0, A 用小随机
        if self.r > 0:
            nn.init.zeros_(self.lora_B)
            nn.init.kaiming_uniform_(self.lora_A, a=math.sqrt(5))

    def forward(self, x):
        """
        x: [B, ..., in_features]
        """
        if self.fan_in_fan_out:
            # 可选：某些实现里 weight 是 [in_features, out_features]
            weight = self.weight.t()
        else:
            weight = self.weight

        # 基础线性部分
        result = F.linear(x, weight, self.bias)

        if self.r > 0 and not self.merged:
            # LoRA 增量：B ( A (Dropout(x))^T )^T
            # 这里用 x @ A^T 再 @ B^T
            lora_x = self.lora_dropout(x)              # [B, ..., in_features]
            # 先乘 A^T: [in_features, r]
            lora_x = lora_x @ self.lora_A.t()          # [B, ..., r]
            # 再乘 B^T: [r, out_features]
            lora_x = lora_x @ self.lora_B.t()          # [B, ..., out_features]
            result = result + self.scaling * lora_x

        return result

    @torch.no_grad()
    def merge_lora(self):
        """
        将 LoRA 权重 merge 回原始 weight
        """
        if self.r > 0 and not self.merged:
            if self.fan_in_fan_out:
                delta_w = (self.scaling * (self.lora_B @ self.lora_A)).t()
            else:
                delta_w = self.scaling * (self.lora_B @ self.lora_A)
            self.weight += delta_w
            self.merged = True

    @torch.no_grad()
    def unmerge_lora(self):
        """
        撤销 merge，用于继续训练 LoRA
        """
        if self.r > 0 and self.merged:
            if self.fan_in_fan_out:
                delta_w = (self.scaling * (self.lora_B @ self.lora_A)).t()
            else:
                delta_w = self.scaling * (self.lora_B @ self.lora_A)
            self.weight -= delta_w
            self.merged = False

五、LoRA 集成到 Transformer Block

class LoRAAttention(nn.Module):
    def __init__(self, d_model, num_heads, r=8, lora_alpha=8, lora_dropout=0.05):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads

        assert d_model % num_heads == 0

        # 对 Q/K/V/O 全部用 LoRALinear
        self.q_proj = LoRALinear(d_model, d_model, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout)
        self.k_proj = LoRALinear(d_model, d_model, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout)
        self.v_proj = LoRALinear(d_model, d_model, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout)
        self.o_proj = LoRALinear(d_model, d_model, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout)

    def forward(self, x, attn_mask=None):
        B, L, _ = x.size()

        Q = self.q_proj(x)  # [B, L, d_model]
        K = self.k_proj(x)
        V = self.v_proj(x)

        def split_heads(t):
            return t.view(B, L, self.num_heads, self.head_dim).transpose(1, 2)
        Q = split_heads(Q)  # [B, H, L, Dh]
        K = split_heads(K)
        V = split_heads(V)

        scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5)
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask == 0, float('-inf'))
        attn = F.softmax(scores, dim=-1)

        out = attn @ V   # [B, H, L, Dh]
        out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
        out = self.o_proj(out)
        return out

六、用 HuggingFace PEFT 做 LLM LoRA 微调

最后给一个 PEFT + Transformers 的最小样例，你可以按自己习惯改成 Qwen / LLaMA / DeepSeek 模型。

from transformers import AutoModelForCausalLM, AutoTokenizer, TrainingArguments, Trainer
from peft import LoraConfig, get_peft_model, TaskType

model_name = "meta-llama/Llama-3-8b"  # 举例，自己换成本地/镜像地址
tokenizer = AutoTokenizer.from_pretrained(model_name)

# 1. 加载基座模型（可以配合 4bit 量化做 QLoRA）
model = AutoModelForCausalLM.from_pretrained(
    model_name,
    device_map="auto",
    torch_dtype="auto",
    # quantization_config=... # 这里可换成 QLoRA 配置
)

# 2. 定义 LoRA 配置
lora_config = LoraConfig(
    task_type=TaskType.CAUSAL_LM,
    r=8,
    lora_alpha=16,
    lora_dropout=0.05,
    bias="none",
    target_modules=[
        "q_proj", "k_proj", "v_proj", "o_proj",  # 根据具体模型模块名调整
    ],
)

# 3. 将模型包一层 PEFT
model = get_peft_model(model, lora_config)
model.print_trainable_parameters()  # 可以看到只训练 LoRA 参数

# 4. 准备数据（示意）
def preprocess(example):
    prompt = example["instruction"]
    response = example["output"]
    text = f"### 指令:\n{prompt}\n\n### 回答:\n{response}"
    tokenized = tokenizer(
        text,
        truncation=True,
        max_length=512,
        padding="max_length",
    )
    # 简单起见，全部 token 都预测，下游按需改 label mask
    tokenized["labels"] = tokenized["input_ids"].copy()
    return tokenized

# dataset = ...  # 自己加载数据，然后 map(preprocess)

# 5. 训练参数
training_args = TrainingArguments(
    output_dir="./lora-llama-sft",
    per_device_train_batch_size=4,
    gradient_accumulation_steps=4,
    learning_rate=1e-4,
    num_train_epochs=3,
    logging_steps=10,
    save_steps=500,
    fp16=True,
)

# 6. Trainer
trainer = Trainer(
    model=model,
    args=training_args,
    train_dataset=train_dataset,  # 预处理后的数据
)

trainer.train()

# 7. 保存 LoRA adapter
model.save_pretrained("./lora-llama-sft")