JavaScript 中的精度丢失与分摊不平问题及解决方案
JavaScript 浮点数精度丢失导致的分摊不平。本文将深入剖析问题根源,并提供经过生产验证的可靠解决方案。方案是否推荐适用场景⚠️ 仅简单场景无严格对账要求整数分摊(分)+Math.floor+ 兜底✅强烈推荐电商、金融、ERP 系统记住:在金钱计算中,永远不要信任浮点数。用“分”做整数运算是行业标准实践。通过上述方法,你可以彻底告别“分摊不平”问题,确保系统在任何金额组合下都保持数据一致性。
文章目录
概述
在前端开发中,尤其是涉及金额计算(如电商、财务系统)时,我们经常会遇到一个“看似简单却极易出错”的问题:JavaScript 浮点数精度丢失导致的分摊不平。它像一个潜伏在代码深处的幽灵,可能在一次看似寻常的促销活动或财务结算中突然爆发,造成数据对不上、用户投诉甚至资损。
本文将不仅展示问题现象,更会深入剖析其底层的计算机科学根源,并提供一套经过生产环境严苛验证的、图文并茂的可靠解决方案,助你彻底告别这个“幽灵”。
一、问题现象:冰山一角下的“精度陷阱”
几乎所有前端开发者都见过这个经典案例:
console.log(0.1 + 0.2); // 输出: 0.30000000000000004
console.log(0.1 + 0.2 === 0.3); // 输出: false
这 0.00000000000000004 的微小误差,在单次计算中似乎可以忽略。但请想象一个更复杂的场景:金额的累加、比例分摊、多级税费计算。每一次运算都可能引入微小的误差,经过层层叠加和放大,最终导致“分摊总和 ≠ 原始总金额”的严重业务逻辑错误。
一个典型的业务场景:补贴分摊
假设有一个订单总金额为 ¥100,平台需要将 ¥30 的补贴按商品金额比例分摊到 3 个商品上。
| 商品 | 金额(元) | 占比 | 理论分摊(元) | Math.round 四舍五入后(元) |
|---|---|---|---|---|
| A | 33.33 | 33.33% | 9.999 | 10.00 |
| B | 33.33 | 33.33% | 9.999 | 10.00 |
| C | 33.34 | 33.34% | 10.002 | 10.00 |
| 在这个理想情况下,总和恰好是 30.00 元。但如果商品金额组合稍作变化,陷阱就出现了: | ||||
| 商品 | 金额(元) | 占比 | 理论分摊(元) | Math.round 四舍五入后(元) |
| ------ | ----------- | ------ | ---------------- | ------------------------------- |
| A | 33.30 | 33.30% | 9.99 | 9.99 |
| B | 33.30 | 33.30% | 9.99 | 9.99 |
| C | 33.40 | 33.40% | 10.02 | 10.02 |
此时总和 9.99 + 9.99 + 10.02 = 30.00,依然正确。但问题在于,由于浮点数精度问题,计算机实际计算出的 33.30 * 0.333 可能是 9.989999...,33.40 * 0.334 可能是 10.019999...。Math.round 的结果变得不可预测。 |
||||
| 更危险的是“最后一项兜底”的常见做法: |
// 假设前两项分摊后,已分配 29.99
const lastItemShare = totalSubsidy - allocatedAmount; // 30 - 29.99 = 0.01
// 但如果浮点误差导致已分配 30.01 呢?
const lastItemShare = totalSubsidy - allocatedAmount; // 30 - 30.01 = -0.01 (负数!)
一个负数的补贴金额,足以让整个业务逻辑崩溃。
二、根源探寻:IEEE 754 标准下的“先天缺陷”
要解决问题,必先理解其根源。JavaScript 中的所有数字(包括整数)都以 64位双精度浮点数(IEEE 754 标准) 的形式存储。这个标准的设计初衷是为了在有限的内存空间内表示极大范围的数值,但它牺牲了精度。
图解:为什么 0.1 无法被精确表示?
计算机内部使用二进制。就像我们无法在十进制中精确表示 1/3(它等于 0.3333... 无限循环)一样,很多十进制小数也无法在二进制中被精确表示。0.1 的二进制转换过程:
0.1 * 2 = 0.2→ 取整数部分00.2 * 2 = 0.4→ 取整数部分00.4 * 2 = 0.8→ 取整数部分00.8 * 2 = 1.6→ 取整数部分10.6 * 2 = 1.2→ 取整数部分10.2 * 2 = 0.4→ …开始循环
所以,0.1的二进制表示是0.0001100110011001100...,这是一个无限循环小数。
当两个这样的近似值相加时,误差会累积,最终导致 0.1 + 0.2 不再精确等于 0.3。
三、错误方案:为什么 toFixed 和 Math.round 治标不治本?
很多开发者会尝试使用 Number.prototype.toFixed() 或 Math.round() 来解决问题。
(0.1 + 0.2).toFixed(2); // "0.30"
(0.1 + 0.2).toFixed(2) === "0.30"; // true
toFixed 确实可以格式化输出,但它返回的是字符串,且其内部计算依然基于浮点数。更重要的是,在分摊场景中,对每一项分别进行四舍五入,会导致舍入误差的累积。
问题流程图:
结论: 这些方法只能用于最终结果的展示,绝不能用于中间过程的计算。
四、黄金法则:整数运算——以“分”为单位治本
金融和电商领域的标准实践是:永远不要用浮点数进行金额计算。
核心思想:将所有金额乘以 100,转换为最小的货币单位(如“分”),然后全程使用整数进行运算,最后再将结果除以 100 转回“元”。
整数在 JavaScript 中是安全的(只要不超过Number.MAX_SAFE_INTEGER),可以保证加减乘除的精确性。
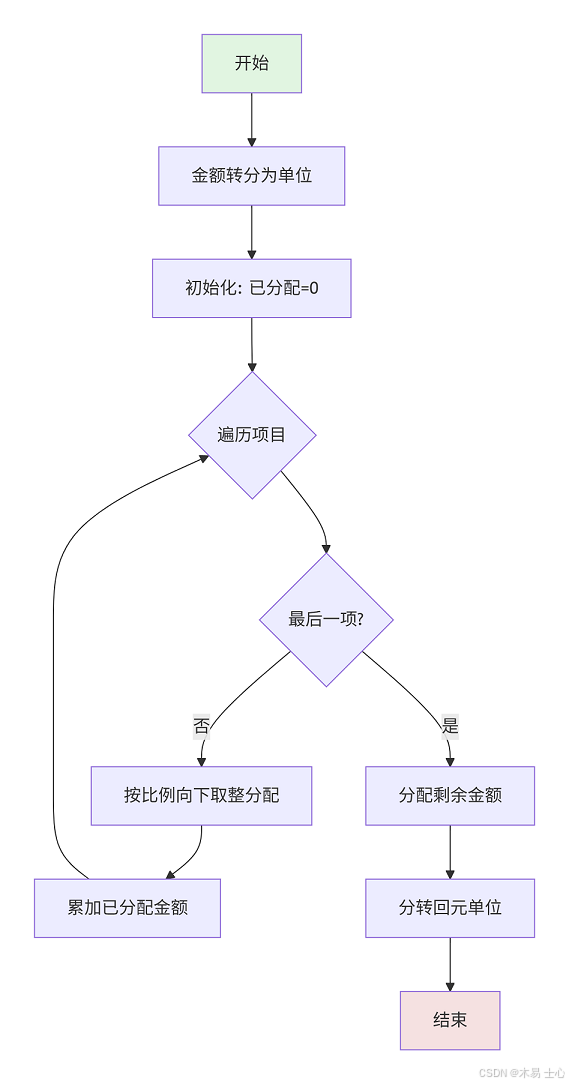
1.算法详解:整数分摊法
为了保证分摊后的总和严格等于原始总额,并避免出现负数,我们采用 “向下取整 + 最后一项兜底” 的策略。
- 转为整数:将所有金额(元)转换为“分”。
- 保守分配:遍历列表,对非最后一项,按比例计算其份额,并使用
Math.floor()向下取整。这确保了每一项分配的金额都不会“超支”。 - 累加已分配:记录已经分配出去的总金额。
- 最后一项兜底:最后一项的份额 = 总金额 - 已分配金额。这个操作可以吸收前面所有
Math.floor()造成的舍去误差,确保总和精确。
算法流程图:
五、代码实现:生产级 TypeScript 方案
下面是一个健壮的、带有完整类型注解和注释的 TypeScript 实现。
/**
* 将金额按比例精确分摊到多个项目上,确保总和严格等于原始金额。
*
* @param totalAmountCents 需要分摊的总金额(单位:分,整数)
* @param itemAmountsInYuan 各个项目的基准金额数组(单位:元,用于计算比例)
* @returns 分摊后的金额数组(单位:元,保留两位小数)
*/
export function distributeAmountPrecisely(
totalAmountCents: number,
itemAmountsInYuan: number[]
): number[] {
// --- 1. 防御性校验 ---
if (totalAmountCents <= 0 || itemAmountsInYuan.length === 0) {
return new Array(itemAmountsInYuan.length).fill(0);
}
// --- 2. 转换为整数(分)---
const itemAmountsInCents = itemAmountsInYuan.map(amount => Math.round(amount * 100));
const totalItemAmountInCents = itemAmountsInCents.reduce((sum, cents) => sum + cents, 0);
if (totalItemAmountInCents === 0) {
return new Array(itemAmountsInYuan.length).fill(0);
}
// --- 3. 核心分摊逻辑 ---
let allocatedCents = 0;
const distributedAmountsInYuan: number[] = [];
itemAmountsInCents.forEach((itemCents, index) => {
let shareCents = 0;
if (index === itemAmountsInCents.length - 1) {
// 最后一项:兜底所有剩余金额,吸收所有舍入误差
shareCents = totalAmountCents - allocatedCents;
} else {
// 非最后一项:按比例计算份额并向下取整,保证不超分
// 注意:这里的乘法是整数乘法,精确无误
shareCents = Math.floor((totalAmountCents * itemCents) / totalItemAmountInCents);
allocatedCents += shareCents;
}
// 将结果从分转回元,并保留两位小数
distributedAmountsInYuan.push(shareCents / 100);
});
return distributedAmountsInYuan;
}
// --- 使用示例 ---
const totalSubsidy = 30; // 30元补贴
const goodsAmounts = [33.33, 33.33, 33.34]; // 商品金额
const shares = distributeAmountPrecisely(totalSubsidy * 100, goodsAmounts);
console.log(shares); // 输出: [10, 10, 10]
console.log(shares.reduce((s, a) => s + a, 0).toFixed(2)); // 输出: "30.00"
const goodsAmounts2 = [33.30, 33.30, 33.40];
const shares2 = distributeAmountPrecisely(totalSubsidy * 100, goodsAmounts2);
console.log(shares2); // 输出: [9.99, 9.99, 10.02]
console.log(shares2.reduce((s, a) => s + a, 0).toFixed(2)); // 输出: "30.00"
六、扩展与思考
- 超大金额处理:JavaScript 的
Number.MAX_SAFE_INTEGER(即2^53 - 1) 约等于 9 quadrillion。如果业务涉及超过此数值的金额(以分为单位),应考虑使用BigInt。 - 第三方库的选择:对于极其复杂的财务计算(如复利、税率),可以考虑使用专门的库,如
decimal.js,big.js。它们实现了任意精度的十进制运算,但会带来额外的性能开销和包体积。对于绝大多数前端分摊场景,整数法是性能和简洁性的最佳平衡。 - 显示与计算分离:始终记住,计算用整数,显示用格式化。在模板中,使用
price.toFixed(2)或过滤器来保证显示两位小数,但底层的数据模型应始终以分为单位存储或计算。
七、总结
| 方案 | 推荐指数 | 核心思想 | 优点 | 缺点 |
|---|---|---|---|---|
toFixed / Math.round |
⭐️ | 格式化或单项四舍五入 | 简单直接 | 无法解决累积误差,易导致分摊不平 |
| 整数分摊法(分) | ⭐️⭐️⭐️⭐️⭐️ | 转为整数,Math.floor + 最后一项兜底 |
精度100%保证,总和严格相等,无负数风险 | 需要转换单位,代码稍复杂 |
| 第三方高精度库 | ⭐️⭐️⭐️ | 使用任意精度对象 | 功能强大,适合复杂金融模型 | 性能开销大,增加依赖 |
最终建议:在处理前端金额分摊时,请将“整数分摊法”作为你的首选和标准实践。 它不仅解决了问题,更体现了一种严谨、可靠的工程思维。通过拥抱整数,我们可以从根本上规避 JavaScript 浮点数带来的陷阱,构建出经得起考验的财务应用。
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容









所有评论(0)