K-means聚类基本概念

K-means是一种基于距离的划分聚类方法，通过迭代将数据划分为K个簇。核心思想是使簇内样本的平方误差最小化。算法流程包括初始化聚类中心、分配样本到最近中心、重新计算中心位置，直到收敛。

聚类簇数 K

K 是 K-means 算法中唯一需要提前指定的超参数，代表着我们希望将数据集划分成的簇的数量。例如，在客户分群场景中，如果我们认为客户可以分为高价值、中价值、低价值三类，那么 K 就可以设为 3。这个参数的选择直接决定了聚类结果的结构，选得过大可能导致簇的过度细分（如将高价值客户再拆分为多个相似簇），选得过小则可能无法捕捉数据的真实分布（如将高、中价值客户合并为一个簇）

通俗的说，就是需要分成几类，聚成几个簇，k的值就是几

距离度量方式

 K-means 一般采用欧氏距离

常见的距离度量方式还有曼哈顿距离

曼哈顿距离：也叫城市街区距离，计算的是样本点在各个维度上的绝对差值之和，公式为

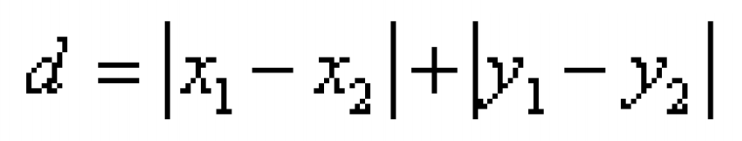
欧式距离：这是最常用的距离度量，适用于连续型数据，计算两个样本点\(x(x_1,y_1)\)和\(x(x_2,y_2)\)之间的直线距离，公式为

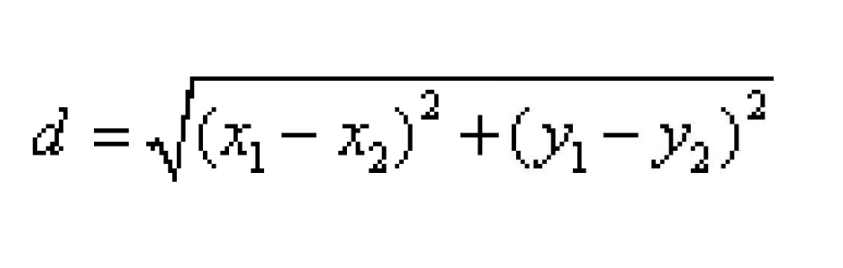
质心

质心是 K-means 算法中簇的核心代表，指的是一个簇内所有样本向量在各个维度上的均值。例如，一个包含三个二维样本 (1,2)、(3,4)、(5,6) 的簇，其质心坐标为

注意：质心并非数据集中的实际样本点，而是算法动态计算出的虚拟点，它的位置会随着迭代过程不断更新，最终稳定在簇的中心位置。

简单来说就是各向量的均值

优化目标

K-means 的优化目标非常明确：最小化所有样本到其所属簇质心的平方距离之和，公式如下：

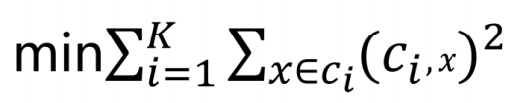
其中ci表示第 i 个簇的质心，x表示簇内的样本点，表示样本到质心的距离（通常为欧氏距离）。这个目标函数也被称为 “惯性”（Inertia），它衡量了簇内样本的紧凑程度，惯性越小，说明簇内样本越集中，聚类效果越好。

K-means 算法步骤拆解

K-means 算法的逻辑非常简洁，核心围绕 “初始化质心→分配样本→更新质心” 三个步骤迭代进行，直到满足停止条件。具体流程如下：

步骤 1：初始化 K 个质心

这是算法的起始步骤，需要从数据集中随机选择 K 个样本点作为初始质心。这里的 “随机” 并非完全无规则，若初始质心选择不当（如过于集中在数据的某个局部区域），可能导致算法收敛到局部最优解，而非全局最优。为了避免这种情况，实际应用中常采用 “K-means++” 初始化方法：首先随机选择一个样本作为第一个质心，之后每个新质心的选择都优先考虑与已选质心距离较远的样本，从而保证初始质心的分散性，提升算法收敛效率和聚类质量。

步骤 2：分配样本到最近簇

对于数据集中的每个样本，计算它与 K 个质心的距离（默认欧氏距离），并将该样本分配到距离最近的质心所在的簇中。这一步完成后，所有样本都被划分到了 K 个簇中的某一个，形成了初始的聚类结果。

步骤 3：更新各簇质心

针对每个簇，重新计算其质心 —— 即簇内所有样本在每个特征维度上的均值。

步骤 4：判断是否收敛

收敛的判断条件通常有两个：一是质心的位置变化小于预设的阈值（如质心在各维度上的移动距离之和小于 1e-5），二是优化目标函数（惯性）的值不再明显下降。如果满足收敛条件，则算法停止，输出最终的聚类结果；否则，返回步骤 2，重新进行样本分配和质心更新，直到收敛。

聚类效果评价方式：轮廓系数

聚类算法不同于监督学习，没有明确的 “标签” 作为判断依据，因此需要通过特定的评价指标来衡量聚类结果的合理性。轮廓系数（Silhouette Coefficient）是最常用的聚类评价指标之一，其核心思想是综合考虑簇内凝聚度和簇间分离度。公式如下：

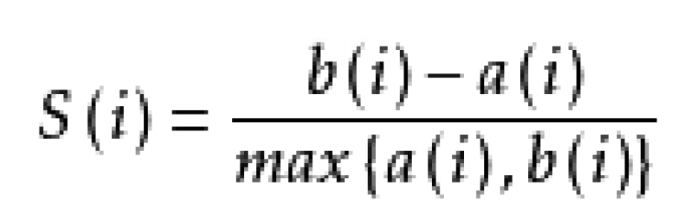
a(i)：对于第 i 个元素 x_i，计算 x_i 与其同一个簇内所有其他元素距离的平均值，表示了簇内的凝聚程度。

a(i)越小，说明该样本与簇内其他样本越相似，簇的凝聚性越好。

b(i)：选取 x_i 外的一个簇，计算 x_i 与该簇内所有点距离的平均距离，遍历其他所有簇，取所有平均值中最小的一个，表示簇间的分离度。

b(i)越大，说明该样本与其他簇的分离程度越高。

计算所有 x 的轮廓系数，求出平均值即为当前聚类的整体轮廓系数。

计算轮廓系数

轮廓系数的公式可分为三种情况：

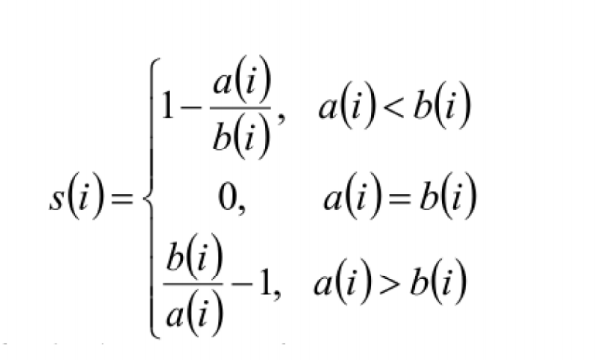
1. 轮廓系数范围在 [-1, 1] 之间。该值越大，越合理。

2.  s(i)  接近 1，则说明样本  i  聚类合理；

3.  s(i)  接近 -1，则说明样本  i  更应该分类到另外的簇；

4. 若  s(i)  近似为 0，则说明样本  i  在两个簇的边界上

典型应用场景

K-means 的应用场景覆盖多个行业，核心是利用无监督学习发现数据的自然分组，常见场景包括：

1. 客户分群：根据用户的消费金额、购买频率、浏览行为等特征，将客户划分为高价值客户、忠诚客户、潜在客户等，为精准营销提供依据；

2. 图像分割：将图像像素按照颜色、亮度等特征聚类，实现前景与背景的分离，或提取图像中的关键物体；

3. 文本聚类：对新闻文章、用户评论等文本数据进行聚类，自动划分主题（如科技、娱乐、财经）；

4. 异常检测：通过聚类识别偏离主要簇的异常样本，例如信用卡欺诈交易、设备故障数据等；

5. 数据预处理：在监督学习任务中，将聚类结果作为特征加入模型，提升模型的泛化能力

案例

import pandas as pd
from sklearn.cluster import KMeans
from sklearn import metrics 


#读取文件
beer = pd.read_table("data.txt",   sep=' ', encoding='utf8', engine='python')
#传入变量（列名）
X = beer[["calories","sodium","alcohol","cost"]]
"""
根据分成不同的簇，自动计算轮廓系数得分
"""
scores = []
for k in range(2,10):#寻找合适的K值
    labels = KMeans(n_clusters=k).fit(X).labels_#从左到右依次进行计算
    score = metrics.silhouette_score(X, labels)#轮廓系数
    scores.append(score) 
print(scores)

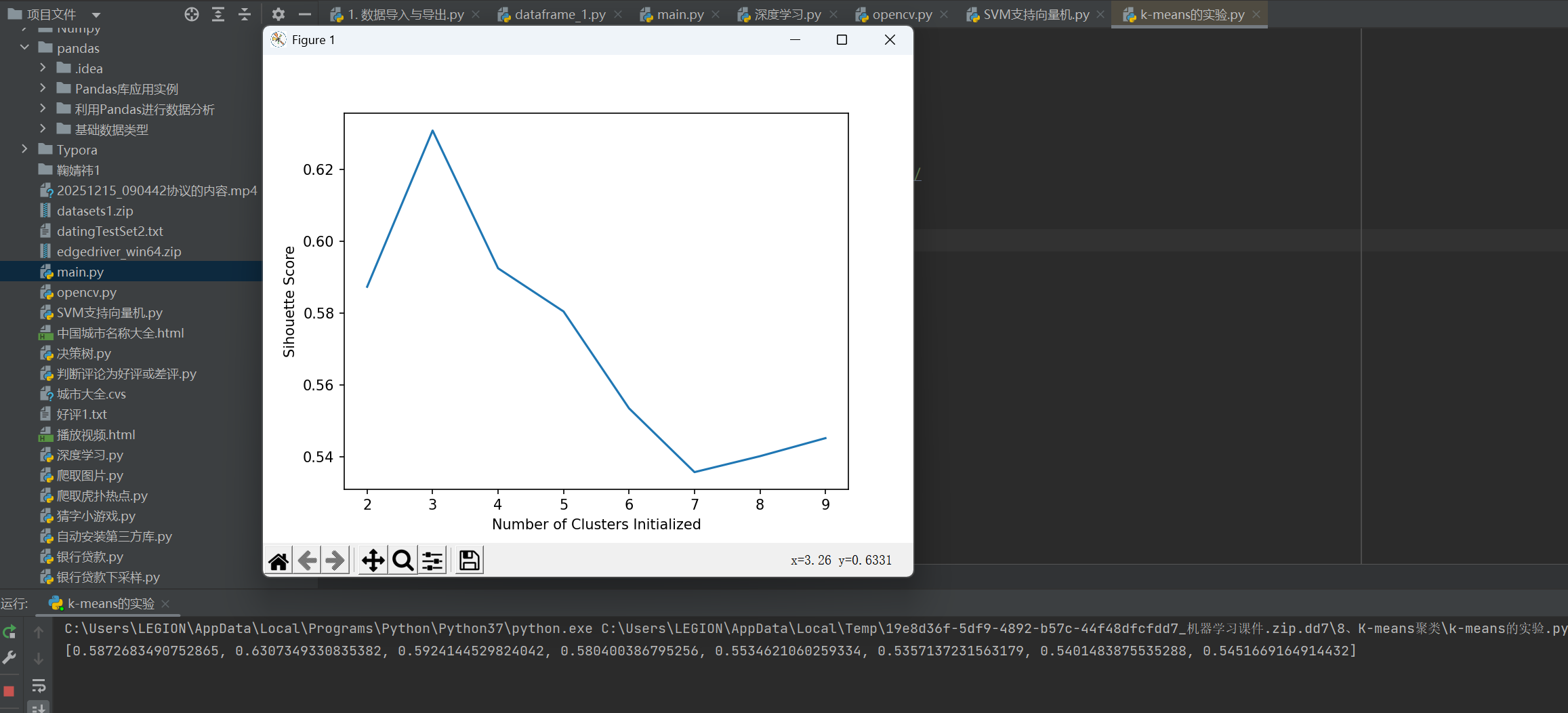
#绘制得分结果
import matplotlib.pyplot as plt


plt.plot(list(range(2,10)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")
plt.show()
#聚类
km = KMeans(n_clusters=2).fit(X)  #K值为2【分为2类】
beer['cluster'] = km.labels_


#对聚类结果进行评分
"""
采用轮廓系数评分
X:数据集   scaled_cluster：聚类结果
score：非标准化聚类结果的轮廓系数
"""
score = metrics.silhouette_score(X,beer.cluster)
print(score)  

运行结果：

K-means的API参数

class sklearn.cluster.KMeans(n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)[source]

【参数：】

n_clusters: 类中心的个数,就是要聚成几类。【默认是8个】

init：参初始化的方法，默认为'k-means++'

(1)'k-means++': 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛.

(2) ‘random’:  随机从训练数据中选取初始质心。

(3) 如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。

n_init: 整形，缺省值=10

用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。

max_iter :

执行一次k-means算法所进行的最大迭代数。

Tol: 与inertia结合来确定收敛条件。

precompute_distances：三个可选值，‘auto’，True 或者 False。

预计算距离，计算速度更快但占用更多内存。

(1)‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。

(2)True：总是预先计算距离。

(3)False：永远不预先计算距离。

verbose：整形，默认值=0

random_state :随机状态

copy_x：布尔型，默认值=True

当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

algorithm:'auto','full' or 'elkan'.默认为'auto'
full:采用经典的EM算法
elkan:通过使用三角不等式从而更有效，但不支持稀疏数据
auto:数据稀疏选择full模式，数据稠密选择elkan模式

【属性】

cluster_centers_: 一个n-clusters*n_features的矩阵，表示聚类中心的坐标

Labels_:

每个点的分类标签。

inertia_：float形

每个点到其簇的质心的距离之和。

n_iter_ : int

迭代次数。