「从“黑箱”预测到“白盒”决策」

目录

01  反事实推断的概念起源

1.1 哲学根源：因果关系的反事实思辨

1.2 统计学演进：从描述性统计到因果推断

1.3 机器学习领域的引入：从预测到决策的必然需求

02  反事实推断为何有助于训练高阶智能模型

2.1 关联≠因果，实现精准因果推理

2.2 提升模型可解释性，解决“黑箱”问题

2.3 增强模型鲁棒性，应对复杂动态环境

2.4 优化决策策略，实现“主动学习”与“长期收益最大化”

03  反事实推断的数学模型

3.1 基础模型：鲁宾潜在结果框架

3.1.1 核心定义与假设

3.1.2 计算方法

3.2 进阶模型：珀尔因果图模型

3.2.1 核心定义与因果层次

3.2.2 反事实推断的计算步骤

3.3 现代模型：基于表示学习的反事实推断模型

04  反事实推理嵌入模型训练的流程

4.1 第一步：数据预处理与因果变量定义

4.2 第二步：模型架构设计与因果约束嵌入

4.3 第三步：训练目标优化与反事实损失设计

4.4 第四步：模型推理与反事实结果生成

4.5 第五步：模型评估与验证

05  总结

5.1 从“关联”走向“因果”的必由之路

5.2 反事实推断是解决模型“黑箱”问题的关键

5.3 数学模型提供了因果量化工具

---

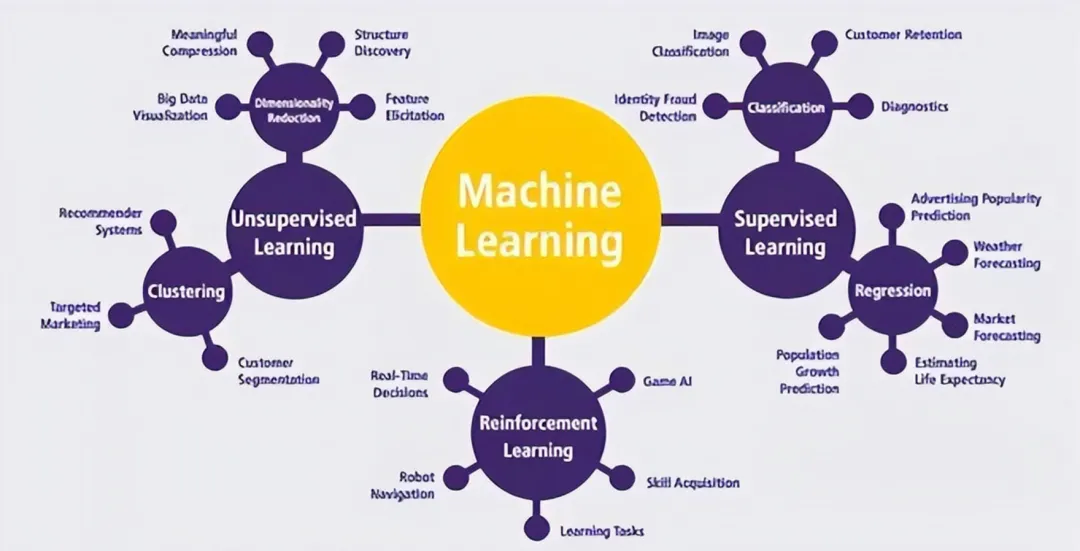
在机器学习（ML）的发展进程中，从早期的统计学习到如今的深度学习、强化学习，模型性能的评价标准逐渐从“预测准确率”向“决策可靠性”“因果可解释性”演进。

在此背景下，“反事实推断”这个源自哲学与统计学的概念，被越来越频繁地引入机器学习。

无论是推荐系统的“若未推荐此商品，用户是否会购买”，还是医疗AI的“若采用另一种治疗方案，患者病情是否会好转”，或是自动驾驶的“若提前0.5秒刹车，是否能避免碰撞”，这些机器学习需要解决的核心决策问题，本质上都是反事实推断问题。

01  反事实推断的概念起源

反事实推断的核心思想是“假设与现实不同的条件，推断可能产生的结果”，其概念起源可追溯至哲学领域的因果关系探讨，后经统计学、经济学等学科的发展，逐渐形成系统化的理论体系，最终被引入机器学习领域。

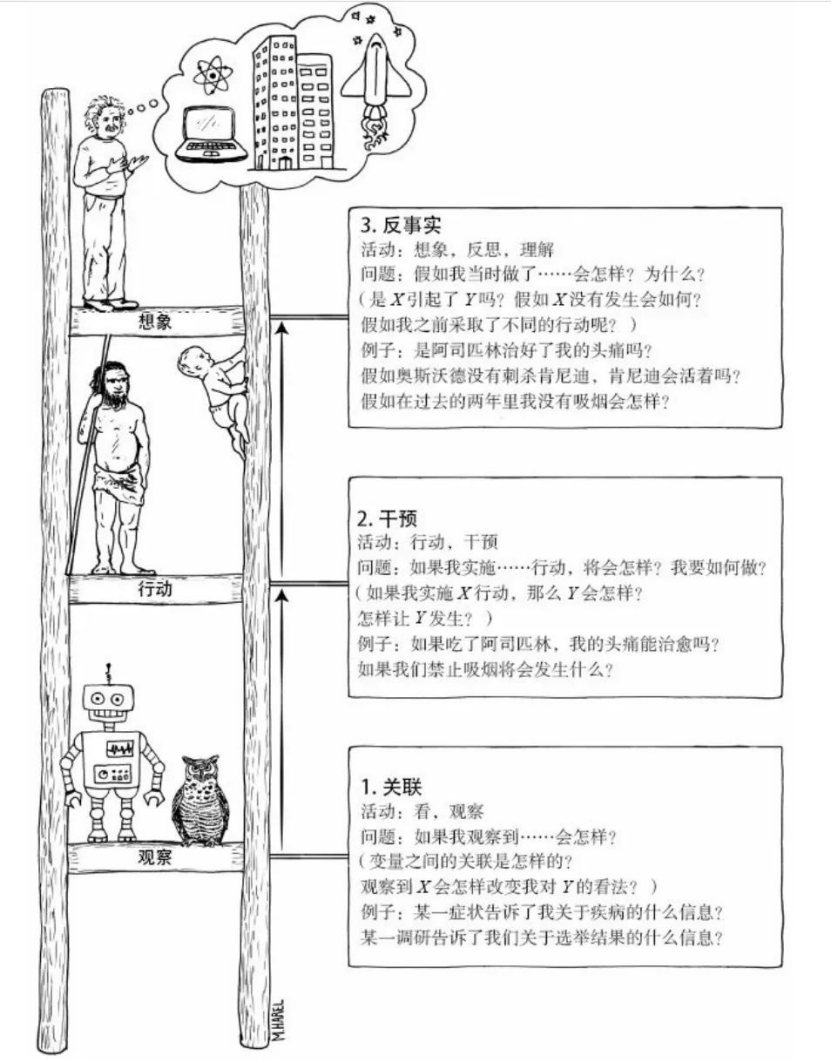
图 | 反事实推理示意图，来自网络

1.1 哲学根源：因果关系的反事实思辨

反事实推断的思想最早可追溯至古希腊哲学家亚里士多德的“四因说”，但其系统化的哲学探讨始于18世纪的苏格兰哲学家大卫·休谟。休谟在《人类理解研究》中提出，因果关系的本质并非事物本身具有的内在属性，而是人类通过观察到“事件A恒常伴随事件B发生”而形成的心理联想。这一观点引发了后续关于“如何界定因果关系”的长期争论，而反事实推断正是这场争论的核心产物。

20世纪初，哲学家大卫·刘易斯在《反事实》一书中首次将反事实推理正式纳入因果关系的分析框架。刘易斯提出，“事件X是事件Y的原因”当且仅当“若X不发生，则Y也不会发生”——这一“反事实依赖性”准则，成为界定因果关系的关键标准。例如，“石头砸破窗户”这一因果关系，可通过反事实推断验证：若石头未砸向窗户（反事实条件），则窗户不会破（反事实结果）。

这一哲学思辨为反事实推断奠定了核心内涵：通过构建与现实世界平行的“反事实世界”，对比现实结果与反事实结果，从而界定因果关系。

哲学领域的反事实推断最初仅停留在逻辑思辨层面，缺乏可量化的分析方法。但核心思想——“通过反事实对比界定因果”，为后续统计学、机器学习领域提供理论。

1.2 统计学演进：从描述性统计到因果推断

20世纪中期，统计学领域的发展推动反事实推断从哲学思辨走向量化分析。早期统计学以描述性统计和预测性统计为主，核心目标是通过数据拟合规律，实现对未来结果的预测。但随着统计学在社会科学、医学等领域的应用深入，研究者发现“预测关联”不等于“因果关系”——例如，“冰淇淋销量与溺水人数正相关”，但二者并非因果关系，而是均受“气温”这一混淆变量影响。这种“关联≠因果”的困境，推动统计学从“关联分析”向“因果分析”转型，反事实推断成为实现这一转型的核心工具。

20世纪80年代，统计学家唐纳德·鲁宾提出“潜在结果框架”（Potential Outcomes Framework），将反事实推断正式量化。鲁宾认为，对于每个个体i，在接受处理（Treatment）T=1和未接受处理T=0时，分别存在两个潜在结果：Y(1)（处理组潜在结果）和Y(0)（控制组潜在结果）。现实中，我们只能观察到其中一个结果（接受处理则观察到Y(1)，否则观察到Y(0)），而另一个未观察到的结果即为“反事实结果”。因果效应（Causal Effect）则定义为潜在结果的差值：τ=i=Y(1)i−Y(0)i。这一框架将反事实推断从哲学概念转化为可计算的统计问题，为后续在机器学习中的应用奠定了理论基础。

1.3 机器学习领域的引入：从预测到决策的必然需求

机器学习领域对反事实推断的引入，始于21世纪初的“可解释性危机”与“决策可靠性需求”。早期机器学习模型（如SVM、随机森林）以预测准确率为核心目标，通过拟合数据中的关联模式实现预测，但这些模型本质上是“黑箱”，无法解释“为何做出该预测”，更无法回答“若采取不同决策，结果会如何”。随着机器学习在医疗、金融、司法等关键领域的应用深入，模型的决策可靠性与因果可解释性成为刚需——例如，医疗AI若仅基于关联模式推荐治疗方案，可能将“病情严重程度”这一混淆变量导致的关联误判为因果，从而推荐无效甚至有害的方案；金融风控模型若仅依赖关联分析，可能因忽视“经济环境”这一混淆变量而做出错误的信贷决策。

为解决这一问题，机器学习研究者开始引入反事实推断的思想，将模型的目标从“预测现实结果”转向“推断反事实结果，优化决策”。例如，在强化学习中，智能体需要通过反事实推断“若采取不同动作，未来奖励会如何变化”，从而优化动作策略；在推荐系统中，通过反事实推断“若推荐其他商品，用户的点击/购买行为会如何”，从而避免“热门商品过度推荐”的偏差。反事实推断的引入，使机器学习模型从“被动预测”走向“主动决策”，成为高阶智能模型的核心支撑。

02  反事实推断为何有助于训练高阶智能模型

高阶智能模型的核心特征是“具备决策能力、可解释性与鲁棒性”，能够在复杂、动态的真实环境中自适应调整策略。反事实推断之所以能助力高阶智能模型的训练，本质上是因为它解决了传统机器学习模型在因果识别、可解释性、鲁棒性等方面的核心缺陷，为模型从“关联拟合”走向“因果推理”提供了关键工具。

2.1 关联≠因果，实现精准因果推理

传统机器学习模型的核心缺陷是“仅能拟合数据中的关联模式，无法识别因果关系”。在真实世界中，数据中的关联往往受到混淆变量、选择偏差等因素的影响，若模型仅基于关联进行决策，极易产生错误。反事实推断通过构建潜在结果框架，能够有效分离“因果关联”与“虚假关联”，帮助模型实现精准的因果推理。

混淆变量（Confounding Variable）是指同时影响自变量（原因）和因变量（结果）的第三个变量，它会导致我们错误地认为自变量和因变量之间存在因果关系，而实际上这种关系可能是由混淆变量引起的。

关键特征是与自变量相关，或与因变量相关，但不是因果链中的中介变量

经典例子：

•冰淇淋销量与溺水事件：表面上看，冰淇淋销量越高，溺水事件越多。但实际上，天气炎热是混淆变量——热天既增加了冰淇淋消费，也增加了游泳人数，从而增加了溺水风险。

•教育水平与健康状况：受教育程度高的人通常更健康，但收入水平可能是混淆变量——高收入既能支持更好的教育，也能提供更好的医疗保健。

选择偏差（Selection Bias）

是指由于样本选择过程中的系统性错误，导致研究样本不能代表目标总体，从而使研究结果产生偏差。

主要类型：

1. 自选择偏差：研究对象自主决定是否参与研究

2. 幸存者偏差：只观察到"存活"下来的样本，忽略了已"消失"的样本

3. 入院率偏差：基于医院患者的研究可能无法推广到一般人群

4. 时间区间偏差：选择特定时间段的数据导致结论偏差

经典例子：

•二战飞机装甲：统计学家亚伯拉罕·沃尔德发现，返航飞机的弹孔主要集中在机翼和机身，但建议加强驾驶舱和引擎装甲。因为那些被击中要害部位的飞机根本没能返航（幸存者偏差）。

•药物疗效研究：如果只招募愿意参与临床试验的患者，这些患者可能本身就更关注健康，导致药物效果被高估（自选择偏差）。

在高阶智能模型中，因果推理能力是实现精准决策的前提。例如，自动驾驶模型需要判断“前方车辆减速”与“碰撞风险”之间的因果关系，而非仅依赖“前方车辆减速后碰撞概率升高”的关联模式——因为在某些场景下（如前方车辆正常停车让行），减速与碰撞风险并无因果关联。反事实推断通过识别真实的因果关系，使模型的决策建立在可靠的逻辑基础上，提升了决策的精准性。

2.2 提升模型可解释性，解决“黑箱”问题

可解释性是高阶智能模型的核心需求之一，尤其是在关键领域的应用中。传统深度学习模型（如深度神经网络）由于参数规模庞大、结构复杂，被称为“黑箱”——即使模型做出了正确的预测，我们也无法解释“为何得出该结论”。反事实推断通过构建“若改变输入特征，输出结果会如何变化”的反事实场景，为模型的可解释性提供了直观的解释路径。

例如，在图像识别模型中，若模型将一张图片识别为“猫”，传统方法难以解释是哪些特征（如耳朵形状、胡须、毛色）导致了这一识别结果。而通过反事实推断，我们可以构建反事实场景：“若将图片中的猫耳朵改为狗耳朵，模型会将其识别为哪种动物？”若模型此时将其识别为“狗”，则可直观得出“耳朵形状是模型识别‘猫’的关键特征”的结论。这种“反事实干预”的方式，将模型的决策逻辑转化为可直观观察的“特征-结果”关联变化，极大地提升了模型的可解释性。

在自然语言处理（NLP）领域，反事实推断同样能提升模型的可解释性。例如，在情感分析模型中，通过反事实干预“将‘优秀’改为‘糟糕’”，观察模型输出情感分数的变化，即可判断“优秀”这一词汇对模型决策的影响程度。这种可解释性不仅有助于提升用户对模型的信任度，更便于研究者发现模型的缺陷（如对某些偏见性词汇的过度依赖），从而优化模型。

2.3 增强模型鲁棒性，应对复杂动态环境

鲁棒性是高阶智能模型在真实环境中稳定运行的关键——真实环境往往存在数据分布偏移、噪声干扰、未见过的场景等问题，传统模型在这些情况下极易失效。反事实推断通过训练模型“思考反事实场景”，使其能够更好地应对环境变化，提升鲁棒性。

具体而言，反事实推断通过构建多样化的反事实场景，扩大了模型的“经验边界”。例如，在自动驾驶模型的训练中，传统方法仅基于真实的交通场景数据进行训练，若遇到“突发的行人横穿马路”这一未见过的场景，模型可能无法做出正确决策。而通过反事实推断，我们可以基于现有数据生成大量反事实场景：“若在当前场景中突然出现行人，模型应如何调整车速与方向？”“若当前场景下路面湿滑，刹车距离会如何变化？”通过对这些反事实场景的训练，模型能够学习到更通用的决策规则，而非仅拟合真实场景中的关联模式，从而在遇到未见过的场景时，仍能做出稳定、可靠的决策。

此外，反事实推断还能帮助模型应对数据分布偏移问题。在推荐系统中，用户的偏好会随时间变化（如季节变化、消费能力提升），导致训练数据的分布与真实环境中的数据分布不一致，传统推荐模型的性能会显著下降。通过反事实推断，模型可以推断“若用户偏好发生某种变化，其点击/购买行为会如何变化”，从而自适应调整推荐策略，提升在分布偏移场景下的鲁棒性。

2.4 优化决策策略，实现“主动学习”与“长期收益最大化”

高阶智能模型的核心目标之一是“通过决策实现收益最大化”，尤其是在强化学习、动态推荐等领域，模型需要通过持续的决策与环境交互，实现长期收益的最大化。反事实推断通过帮助模型“反思”不同决策的潜在结果，实现决策策略的优化，推动模型从“被动拟合”走向“主动学习”。

在强化学习中，智能体的决策过程是“观察环境状态→采取动作→获得奖励→更新策略”。传统强化学习模型通过“试错”的方式更新策略，即只有当采取某种动作后，才能观察到对应的奖励，这种方式不仅效率低下，还可能在试错过程中产生严重的负面后果（如自动驾驶模型试错时发生碰撞）。反事实推断则可以帮助智能体在采取动作前，通过推断“若采取不同动作，会获得何种奖励”，提前筛选出最优动作，减少试错成本。例如，在游戏AI的训练中，通过反事实推断，AI可以提前预测“若选择向左移动，会被敌人攻击；若选择向右移动，会获得道具”，从而直接选择向右移动的最优动作，提升训练效率与决策效果。

在动态推荐系统中，反事实推断同样能优化决策策略。传统推荐模型往往基于用户的历史行为推荐相似商品，容易导致“信息茧房”问题，同时无法考虑推荐策略对用户长期兴趣的影响。通过反事实推断，模型可以推断“若推荐多样化的商品，用户的长期活跃度会如何变化”，从而调整推荐策略，在短期点击收益与长期用户留存之间实现平衡，实现长期收益的最大化。

03  反事实推断的数学模型

反事实推断的数学模型体系以鲁宾的“潜在结果框架”为基础，结合图灵奖得主朱迪亚·珀尔的“因果图模型”，形成了“潜在结果+因果图”的二元体系。此外，随着机器学习的发展，研究者还提出了基于表示学习的反事实推断模型，以应对高维数据场景。本节将系统梳理这三类核心数学模型的原理、假设与计算方法。

3.1 基础模型：鲁宾潜在结果框架

鲁宾潜在结果框架是反事实推断的基础数学模型，其核心思想是通过定义“潜在结果”，将反事实推断转化为“缺失数据填补”问题。该框架的核心假设与数学定义如下：

3.1.1 核心定义与假设

定义1：潜在结果。对于每个个体i（i=1,2,...,n），存在两个潜在结果：Y(1)i（个体i接受处理T=1时的结果）和Y(0)i（个体i未接受处理T=0时的结果）。现实中，我们只能观察到其中一个结果，记为观察结果Yi=Yi(1)·Ti+Yi(0)·(1−Ti)，其中Ti为处理变量（Ti=1表示接受处理，Ti=0表示未接受处理）。未观察到的潜在结果即为反事实结果。

定义2：因果效应。因果效应分为个体因果效应（ITE）和平均因果效应（ATE）。个体因果效应为τi=Y(1)i−Y(0)i；由于个体因果效应无法直接计算（无法同时观察到Y(1)i和Y(0)i），实际应用中通常关注平均因果效应：ATE=E[Y(1)−Y(0)]，即所有个体因果效应的期望。此外，还可能关注处理组平均因果效应（ATT=E[Y(1)−Y(0)|T=1]）和控制组平均因果效应（ATC=E[Y(1)−Y(0)|T=0]）。

核心假设：为了计算平均因果效应，潜在结果框架需要满足三个关键假设：

1. 稳定单位处理值假设（SUTVA）：每个个体的潜在结果不受其他个体处理状态的影响，且处理水平是唯一的。例如，在药物疗效研究中，患者A的疗效不受患者B是否服药的影响，且“服药”这一处理只有“服用”和“不服用”两种水平。

2. 可忽略性假设（Ignorability）：处理变量T与潜在结果（Y(1),Y(0)）在给定协变量X的条件下相互独立，即(T⊥Y(1),Y(0)|X)。这一假设意味着，在控制了协变量X后，接受处理和未接受处理的个体在潜在结果上是可比的，从而可以通过“匹配”或“加权”的方式填补反事实结果。

3. 正值假设（Positivity）：对于所有X的取值，都有0<P(T=1|X)<1。这一假设确保了对于每个协变量水平的个体，都存在接受处理和未接受处理的样本，从而可以通过这些样本来估计反事实结果。

其中协变量（Covariate）是指在统计分析或实验研究中，除了主要关注的自变量（解释变量）和因变量（响应变量）之外，其他可能影响因变量的变量。也被称为控制变量、混杂变量（当它与自变量相关时）或预测变量。

自变量 vs 协变量：自变量是研究者主要关注的变量，协变量是为了控制混杂而引入的

协变量 vs 混淆变量：所有混淆变量都是协变量，但并非所有协变量都是混淆变量（只有当协变量同时影响自变量和因变量时才是混淆变量）

3.1.2 计算方法

在满足上述假设的前提下，平均因果效应可以通过以下方法计算：

1. 匹配法（Matching）：核心思想是为每个接受处理的个体，找到一个或多个协变量X相似的未接受处理的个体，用未接受处理个体的观察结果作为接受处理个体的反事实结果（反之亦然），然后计算两组结果的差值作为平均因果效应。常见的匹配方法包括最近邻匹配、倾向得分匹配（将高维协变量X压缩为一维倾向得分P(T=1|X)，基于倾向得分进行匹配）等。

2. 加权法（Weighting）：通过给样本赋予权重，使处理组和控制组在协变量X上的分布一致，从而直接估计平均因果效应。例如，逆概率加权（IPW）方法通过权重w=Ti/P(T=1|X)+(1−Ti)/(1−P(T=1|X))，将样本加权为“理想随机对照试验”样本，此时平均因果效应可表示为ATE=E[w·Yi]。

3. 回归方法（Regression）：通过构建回归模型，将观察结果Yi与处理变量T和协变量X拟合，即Yi=α+β·Ti+γ·X+ε，其中β即为平均因果效应的估计值。回归方法的核心假设是潜在结果与协变量之间存在线性关系，适用于协变量较少的场景。

3.2 进阶模型：珀尔因果图模型

鲁宾潜在结果框架的局限性在于，它无法明确处理变量、协变量与结果变量之间的因果关系结构，难以识别混淆变量和工具变量。为解决这一问题，朱迪亚·珀尔提出了因果图模型（Causal Graph Model），通过有向无环图（DAG）直观地表示变量之间的因果关系，为反事实推断提供了“因果结构先验”，从而更精准地识别因果效应。

3.2.1 核心定义与因果层次

定义3：因果图。因果图是一个有向无环图G=(V,E)，其中V是变量集合（包括处理变量T、结果变量Y、协变量X等），E是有向边，表示变量之间的直接因果关系。例如，若存在有向边X→T和X→Y，则表示X是T和Y的混淆变量（同时影响处理变量和结果变量）。

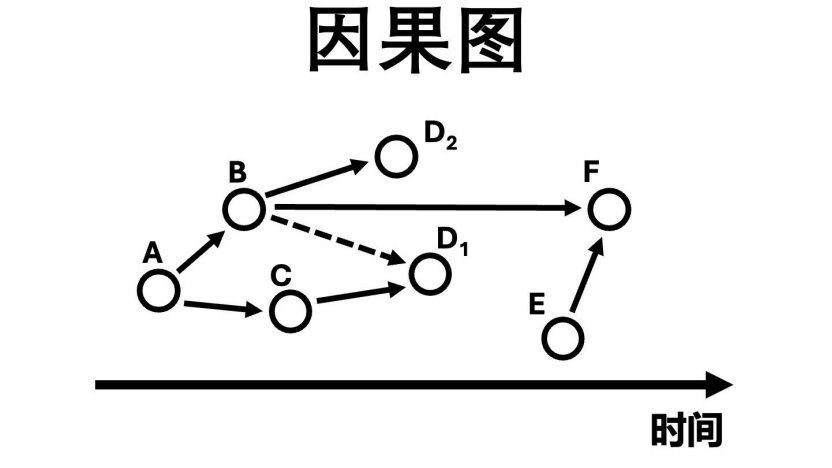
珀尔提出的“因果层次阶梯”（Causal Hierarchy）将因果推断分为三个层次，反事实推断处于最高层次：

1. 关联层（Association）：关注变量之间的关联关系，如P(Y|X)（给定X时Y的条件概率），对应传统机器学习的预测任务。

2. 干预层（Intervention）：关注“若干预变量X，结果Y会如何变化”，如P(Y|do(X=x))（干预X为x时Y的条件概率），对应强化学习中的动作干预。

3. 反事实层（Counterfactual）：关注“若过去的变量X发生变化，结果Y会如何变化”，如P(Yx|X=x',Y=y)（在现实中X=x'、Y=y的情况下，若X=x时Y的条件概率），对应反事实推断的核心问题。

3.2.2 反事实推断的计算步骤

基于因果图模型的反事实推断分为三个核心步骤，称为“三层阶梯”步骤：

1. 归因（Abduction）：利用观察数据，估计因果图中各变量的概率分布，尤其是混淆变量的分布。例如，在因果图X→T→Y、X→Y中，通过观察数据估计P(X)、P(T|X)、P(Y|T,X)。

2. 干预（Action）：通过“do算子”干预处理变量T，将因果图中指向T的边删除（确保干预后的T与混淆变量X独立），构建反事实场景下的概率分布。例如，若要推断“若T=0时的反事实结果Y(0)”，则干预T=0，得到P(Y|do(T=0),X)。

3. 预测（Prediction）：基于归因步骤得到的混淆变量分布，对干预后的概率分布进行积分，得到反事实结果的期望，即E[Y(0)]=∫P(Y|do(T=0),X)P(X|观察数据)dX。通过对比E[Y(1)]和E[Y(0)]，即可得到平均因果效应。

因果图模型的优势在于，它能够明确识别混淆变量和工具变量，从而放松潜在结果框架中的可忽略性假设。例如，若存在工具变量Z（仅影响T，不影响Y），则可通过因果图Z→T→Y、X→T→Y识别因果效应，无需控制所有混淆变量X。

3.3 现代模型：基于表示学习的反事实推断模型

随着机器学习的发展，数据维度越来越高（如图像、文本数据），传统的潜在结果框架和因果图模型难以处理高维协变量。为此，研究者提出了基于表示学习的反事实推断模型，核心思想是“将高维协变量映射到低维表示空间，在表示空间中满足潜在结果框架的假设，从而估计因果效应”。

基于表示学习的反事实推断模型的核心假设是：存在一个低维表示空间Z，使得在Z的条件下，处理变量T与潜在结果（Y(1),Y(0)）相互独立（即可忽略性假设在表示空间中成立）。模型通过神经网络学习从高维协变量X到低维表示Z的映射，然后在Z的空间中估计因果效应。

常见的模型结构包括以下两类：

1. 生成式模型：通过生成对抗网络（GAN）等生成模型，学习反事实结果的分布。例如，模型分为生成器和判别器，生成器基于处理变量T和协变量X，生成潜在结果Y(1)和Y(0)；判别器则区分生成的潜在结果与真实观察结果。通过对抗训练，生成器能够学习到精准的潜在结果分布，从而估计因果效应。

2. 判别式模型：通过神经网络直接学习从协变量X和处理变量T到结果Y的映射，同时引入正则化项，确保在表示空间中满足可忽略性假设。例如，在表示学习模块中加入“平衡正则项”，使处理组和控制组在表示空间Z中的分布一致（即P(Z|T=1)=P(Z|T=0)），从而在表示空间中直接估计平均因果效应。

04  反事实推理嵌入模型训练的流程

将反事实推理嵌入机器学习模型训练，需贯穿“数据预处理—模型构建—训练优化—评估验证”全流程。通过“因果约束嵌入”与“反事实场景驱动”，让模型在学习数据模式的同时，掌握因果推理能力。结合前文提及的潜在结果框架、因果图模型及表示学习模型，具体嵌入流程可分为以下五个关键步骤，每个步骤均需适配反事实推理的核心需求。

4.1 第一步：数据预处理与因果变量定义

数据层面的准备是反事实推理嵌入的基础，核心目标是明确因果关系要素，为后续模型训练提供“因果导向”的数据支撑，区别于传统机器学习仅关注特征与标签的预处理逻辑。具体操作包括：

一是明确核心因果变量。根据任务场景界定“处理变量T”“结果变量Y”及“协变量X”：处理变量为模型可干预的决策变量（如推荐系统中“是否推荐某商品”、医疗AI中“是否采用某治疗方案”）；结果变量为需优化的目标变量（如用户购买行为、患者病情指标）；协变量为可能影响处理与结果关系的混淆变量（如用户画像、患者基础病情），需全面筛选以避免遗漏关键混淆因素。

二是数据清洗与平衡处理。针对观测数据中常见的“选择偏差”（如处理组与控制组样本分布不均），需通过数据重采样、倾向得分匹配等方法平衡两组样本的协变量分布（参考3.1.2节匹配法），确保在控制协变量后，处理变量与潜在结果满足可忽略性假设。对于高维数据（如图像、文本），需进行预处理（如特征提取、归一化），为后续表示学习模块提供适配输入。

三是反事实数据增强（可选）。对于数据量不足或场景覆盖不全面的情况，可通过生成模型生成虚拟反事实样本，补充“未观测到的潜在结果”。例如，在自动驾驶数据集中，生成“当前场景突发行人横穿”的反事实样本，丰富模型对极端场景的学习素材。

4.2 第二步：模型架构设计与因果约束嵌入

模型架构是反事实推理嵌入的核心载体，需根据任务类型（传统统计学习、深度学习）与数据维度，选择适配的因果模型框架，并在架构中嵌入因果约束，确保模型学习因果关联而非仅拟合关联模式。具体设计思路分为三类：

一是传统统计学习模型的适配。对于低维数据场景，可基于鲁宾潜在结果框架，在传统模型（如回归、随机森林）中引入因果约束。例如，在线性回归模型中加入“处理变量×协变量”交互项，明确控制协变量后的处理效应；在随机森林中，通过加权样本（参考3.1.2节加权法）让模型聚焦因果关联，抑制虚假关联的干扰。

二是因果图引导的深度学习架构。对于复杂因果结构场景，可将珀尔因果图模型（参考3.2节）与深度学习结合，通过架构设计编码因果关系。例如，在神经网络中加入“因果注意力机制”，让模型重点关注因果图中处理变量到结果变量的直接路径，忽略混淆变量的间接干扰；通过“do算子”模块（模拟干预操作）删除处理变量的输入边，强制模型学习干预后的结果分布，实现反事实推断。

三是高维数据的表示学习架构。对于图像、文本等大维度数据，采用基于表示学习的反事实模型架构。核心是设计“表示学习模块+预测模块”的双阶段结构：表示学习模块通过神经网络将高维协变量映射到低维表示空间Z，并引入平衡正则项（如MMD）确保处理组与控制组在Z中分布一致；预测模块基于Z分别训练处理组（Y(1)）与控制组（Y(0)）的预测器，实现潜在结果的精准估计。

4.3 第三步：训练目标优化与反事实损失设计

传统机器学习以“预测误差最小化”为核心目标，而嵌入反事实推理的模型需新增“因果一致性”损失项，确保模型的预测结果符合反事实逻辑。训练目标通常为“预测损失+因果正则化损失”的组合形式，具体损失设计需适配模型架构：

一是基于潜在结果框架的损失设计。对于匹配法、加权法适配的模型，损失函数需包含“反事实结果预测误差”。例如，在倾向得分匹配模型中，损失项为“观察结果预测误差+匹配样本的反事实结果预测误差”，强制模型精准拟合观察结果与未观察的反事实结果。

二是基于因果图的损失设计。引入“干预一致性损失”，确保模型在“真实观测”与“干预场景”下的预测逻辑一致。例如，在自动驾驶模型中，损失项包含“真实场景下的碰撞风险预测误差”与“do(T=提前刹车)干预场景下的碰撞风险预测误差”，让模型学习干预后的反事实结果规律。

三是基于表示学习的损失设计。核心是“平衡损失+预测损失”的组合。例如，在BRN模型中，平衡损失为处理组与控制组在表示空间Z中的分布差异（如MMD），预测损失为潜在结果Y(1)与Y(0)的预测误差，通过联合优化让模型在平衡表示的基础上精准估计因果效应。

训练过程中，需采用梯度下降法联合优化组合损失，同时监控因果效应估计的稳定性（如ATE的波动范围），避免模型过度拟合观察数据而丧失反事实推理能力。

4.4 第四步：模型推理与反事实结果生成

模型训练完成后，需通过特定的推理逻辑生成反事实结果，为决策优化提供支撑。根据模型架构的不同，推理过程分为两类：

一是直接推理法。适用于潜在结果框架与因果图模型，通过模型直接输出处理组与控制组的潜在结果，计算因果效应（τ=Y(1)-Y(0)），进而生成反事实结论。例如，医疗AI模型直接输出“患者采用方案A（T=1）的治愈率Y(1)=80%”与“未采用方案A（T=0）的治愈率Y(0)=40%”，反事实结论为“若采用方案A，患者治愈率提升40%”。

二是干预推理法。适用于表示学习与深度学习模型，通过对输入特征进行“反事实干预”生成新输入，再通过模型预测得到反事实结果。例如，在图像识别模型中，干预输入特征“将猫耳朵改为狗耳朵”，模型预测结果从“猫”变为“狗”，从而生成反事实结论“耳朵形状是模型识别‘猫’的关键特征”；在推荐系统中，干预输入“将推荐商品A改为商品B”，预测用户点击行为变化，得到“若推荐B，用户点击概率提升25%”的反事实结果。

4.5 第五步：模型评估与验证

嵌入反事实推理的模型评估，需突破传统“预测准确率”的单一标准，新增“因果有效性”与“反事实合理性”评估指标，形成多维度评估体系：

一是预测性能评估。采用传统指标（如准确率、MSE、AUC）评估模型对观察结果的预测精度，确保模型具备基础的拟合能力。

二是因果有效性评估。核心是验证模型估计的因果效应是否可靠，常用指标包括：平均因果效应（ATE）的偏差（与随机对照试验RCT结果对比，RCT为因果效应评估的金标准）、处理组与控制组的协变量平衡度（平衡度越高，因果效应估计越可靠）。对于无RCT数据的场景，可采用“安慰剂测试”（将处理变量替换为随机变量，若模型估计的ATE接近0，则说明模型能有效识别因果关系）。

三是反事实合理性评估。通过人工审核或领域知识验证反事实结果的逻辑合理性。例如，自动驾驶模型生成的“提前0.5秒刹车可避免碰撞”的反事实结论，需符合交通力学规律；医疗AI生成的“更换治疗方案可改善病情”的结论，需符合临床诊疗指南。对于不合理的反事实结果，需回溯至数据预处理或模型设计环节，优化模型参数或因果约束。

此外，还需评估模型在分布偏移、噪声干扰等场景下的鲁棒性（参考2.3节），确保反事实推理能力在真实复杂环境中稳定有效。

05  总结

反事实推断从哲学领域的因果思辨出发，经统计学的量化发展，最终被引入机器学习领域，成为高阶智能模型训练的核心工具。其核心价值在于，解决了传统机器学习模型“关联≠因果”的核心缺陷，为模型提供了因果推理能力、可解释性、鲁棒性与主动决策能力，推动机器学习从“被动预测”走向“主动智能”。本文通过对反事实推断的概念起源、助力高阶智能模型的内在逻辑、数学模型体系的系统梳理，完整解答了“为何ML经常提到反事实推断”这一问题，具体可总结为以下四点：

5.1 从“关联”走向“因果”的必由之路

传统机器学习模型的核心是拟合数据中的关联模式，但在真实世界中，关联往往受到混淆变量、选择偏差等因素的影响，无法支撑可靠的决策。反事实推断通过构建潜在结果框架，分离“因果关联”与“虚假关联”，使模型的决策建立在真实的因果关系基础上。这一转变是机器学习从“实验室中的高准确率”走向“真实环境中的可靠决策”的关键，也是高阶智能模型的核心要求——无论是医疗、金融还是自动驾驶，只有基于因果关系的决策，才能保证安全性与可靠性。

5.2 反事实推断是解决模型“黑箱”问题的关键

随着深度学习模型的发展，“黑箱”问题日益突出，严重制约了机器学习在关键领域的应用。反事实推断通过“反事实干预”的方式，直观地展示“输入特征变化对输出结果的影响”，为模型的可解释性提供了量化的解释路径。例如，在医疗AI中，通过反事实推断可以明确“为何推荐该治疗方案”（若不推荐该方案，患者病情会恶化）；在司法AI中，可以解释“为何给出该量刑建议”（若调整某个量刑因素，量刑结果会如何变化）。这种可解释性不仅提升了用户对模型的信任度，更便于研究者发现模型的缺陷，推动模型的迭代优化。

5.3 数学模型提供了因果量化工具

鲁宾的潜在结果框架将反事实推断转化为“缺失数据填补”问题，珀尔的因果图模型为反事实推断提供了“因果结构先验”，而基于表示学习的反事实推断模型则解决了高维数据场景下的因果效应估计问题。这三类数学模型形成了完整的体系，为机器学习提供了从“因果识别”到“效应估计”的全流程量化工具。无论是传统的统计学习模型，还是现代的深度学习、强化学习模型，都可以基于这一体系引入反事实推断，提升模型性能。