《机器学习导论》第 13 章-核机器
本文系统介绍了核机器(Kernel Machines)的原理与应用,重点讲解了支持向量机(SVM)及其核心技巧。主要内容包括:1)线性可分SVM的最优超平面;2)软边缘SVM处理不可分数据;3)ν-SVM的容错机制;4)核技巧的本质与常见核函数对比;5)自定义核函数的实现方法;6)核机器在分类、回归、排序、异常检测等场景的应用;7)核降维技术KernelPCA。通过可视化对比和可运行代码,直观展示
目录
代码:Kernel PCA 降维对比(PCA vs Kernel PCA)
正文
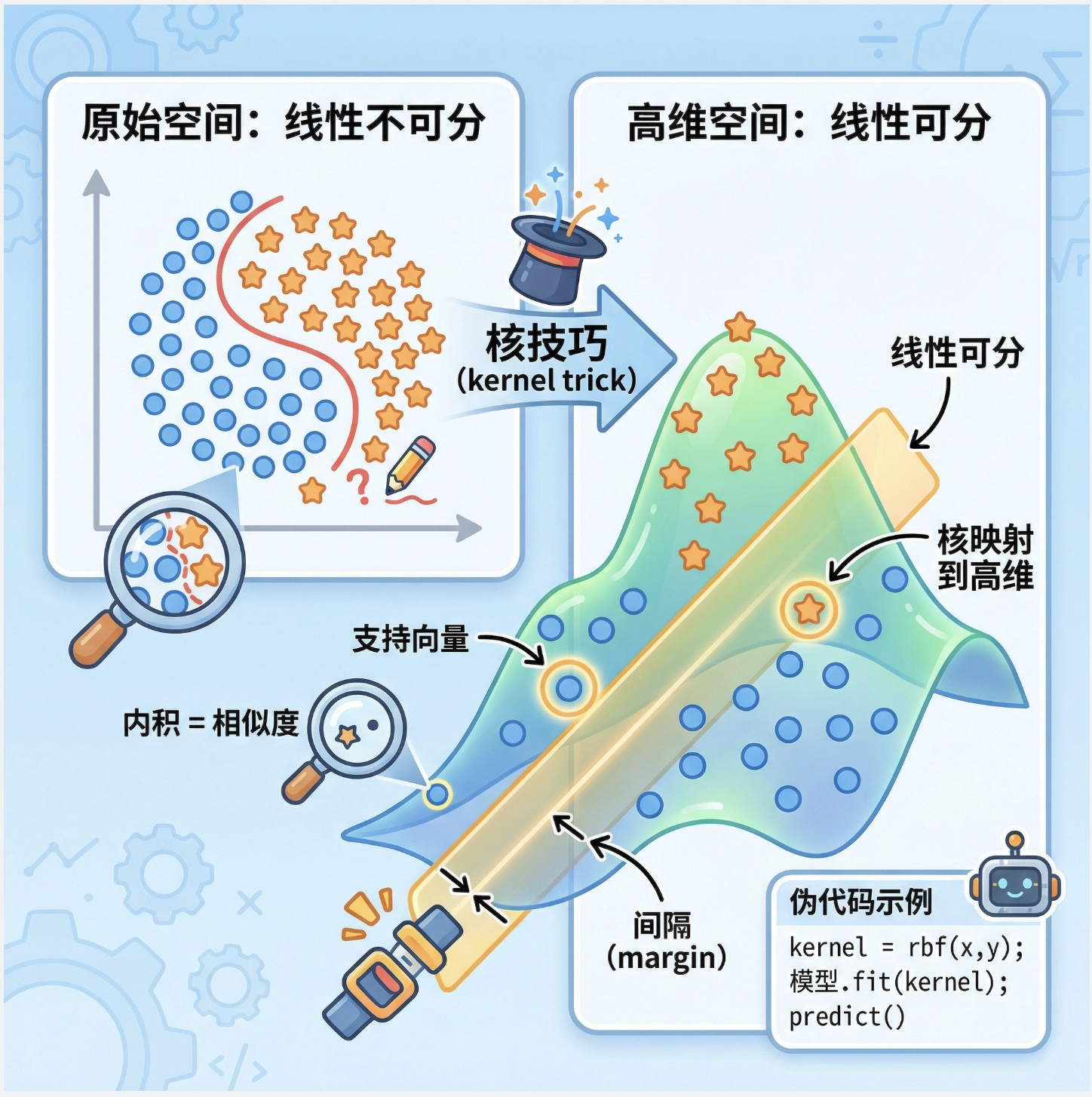
大家好!今天我们来啃《机器学习导论》第 13 章的核心内容 ——核机器(Kernel Machines),核心代表就是我们熟知的 SVM(支持向量机)。很多同学觉得核机器公式多、概念抽象,这篇文章我会用「大白话 + 可视化 + 可直接运行的代码」,把核机器从原理到应用讲透,重点解决 “为什么用核”“核怎么用” 的问题,全程避开复杂公式,只讲核心逻辑!
13.1 引言
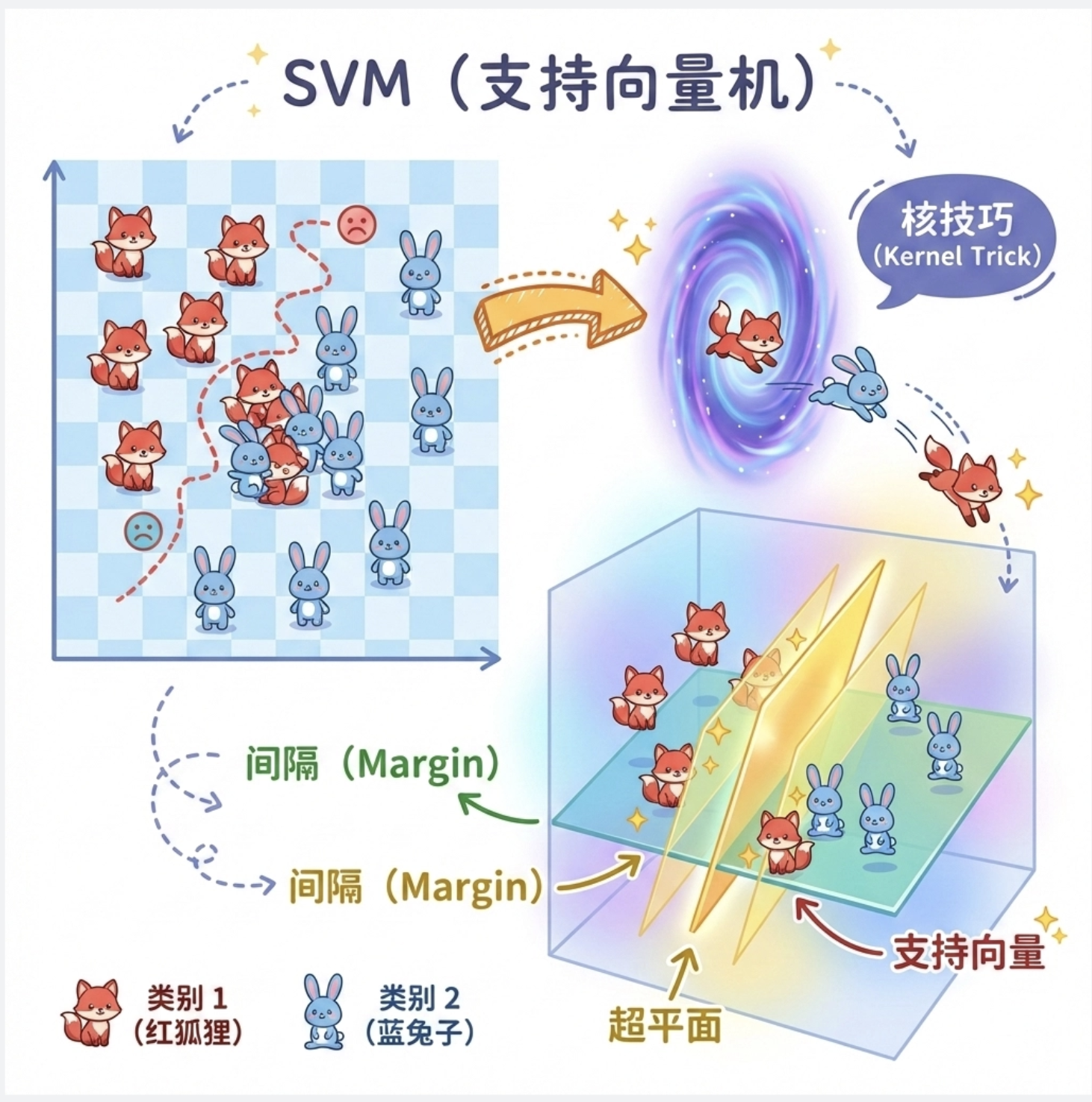
核心概念
核机器(Kernel Machines)是一类基于 “核技巧” 的机器学习算法,核心代表是 SVM(支持向量机)。
你可以把它理解成:找一个最优的 “分界线”(超平面),把不同类别的数据分开,而且这个分界线要尽可能 “公平”—— 离两边的数据都足够远。
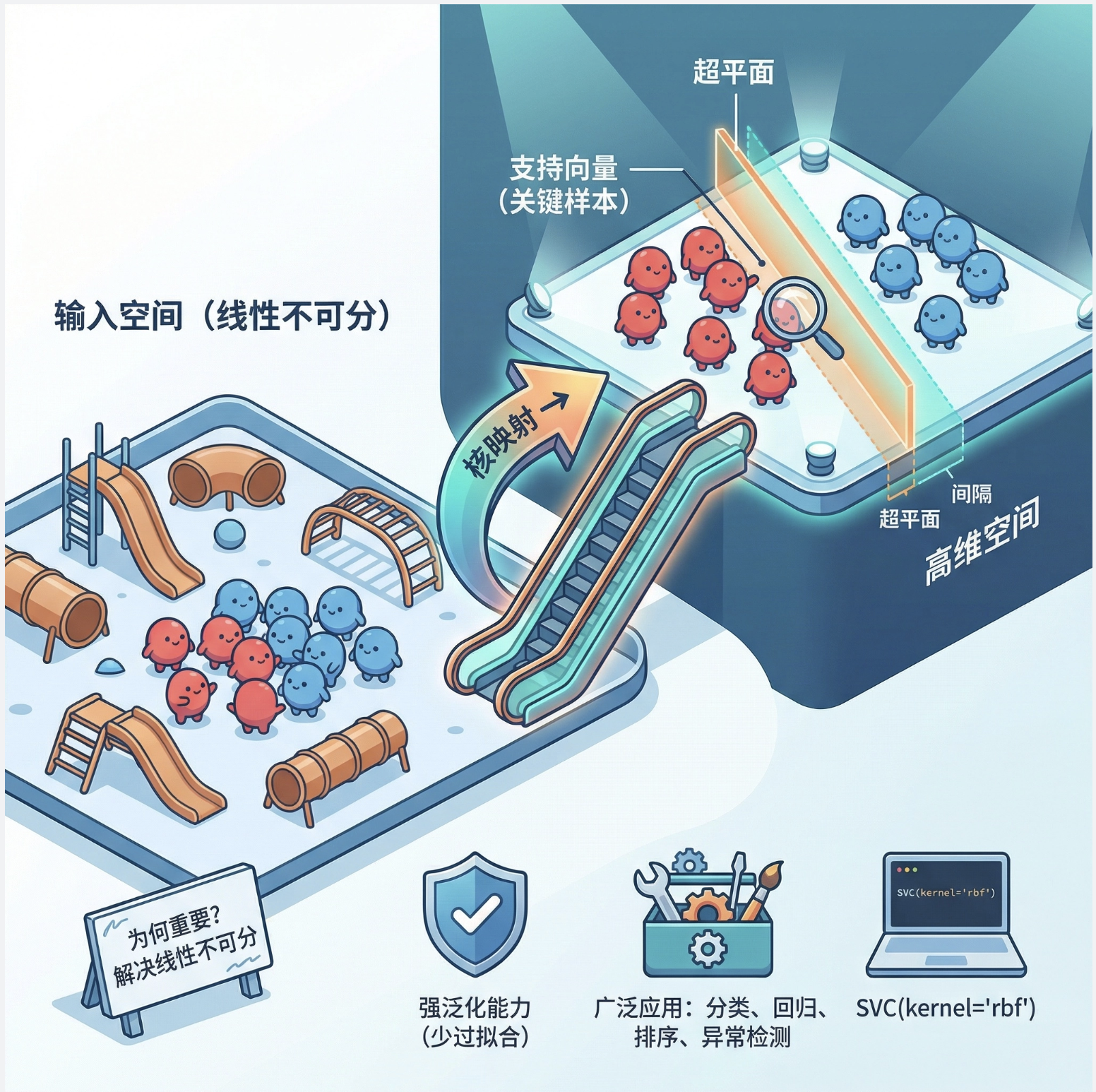
为什么核机器重要?
- 解决线性不可分问题:通过核技巧把低维线性不可分的数据,映射到高维空间变成线性可分
- 泛化能力强:重点关注 “支持向量”(离分界线最近的点),避免过拟合
- 应用广泛:分类、回归、排名、异常检测都能做
先搭环境(必看)
先安装需要的库,后续所有代码都基于这个环境:
pip install numpy scipy scikit-learn matplotlib pandas
13.2 很好分离超平面(线性可分 SVM)
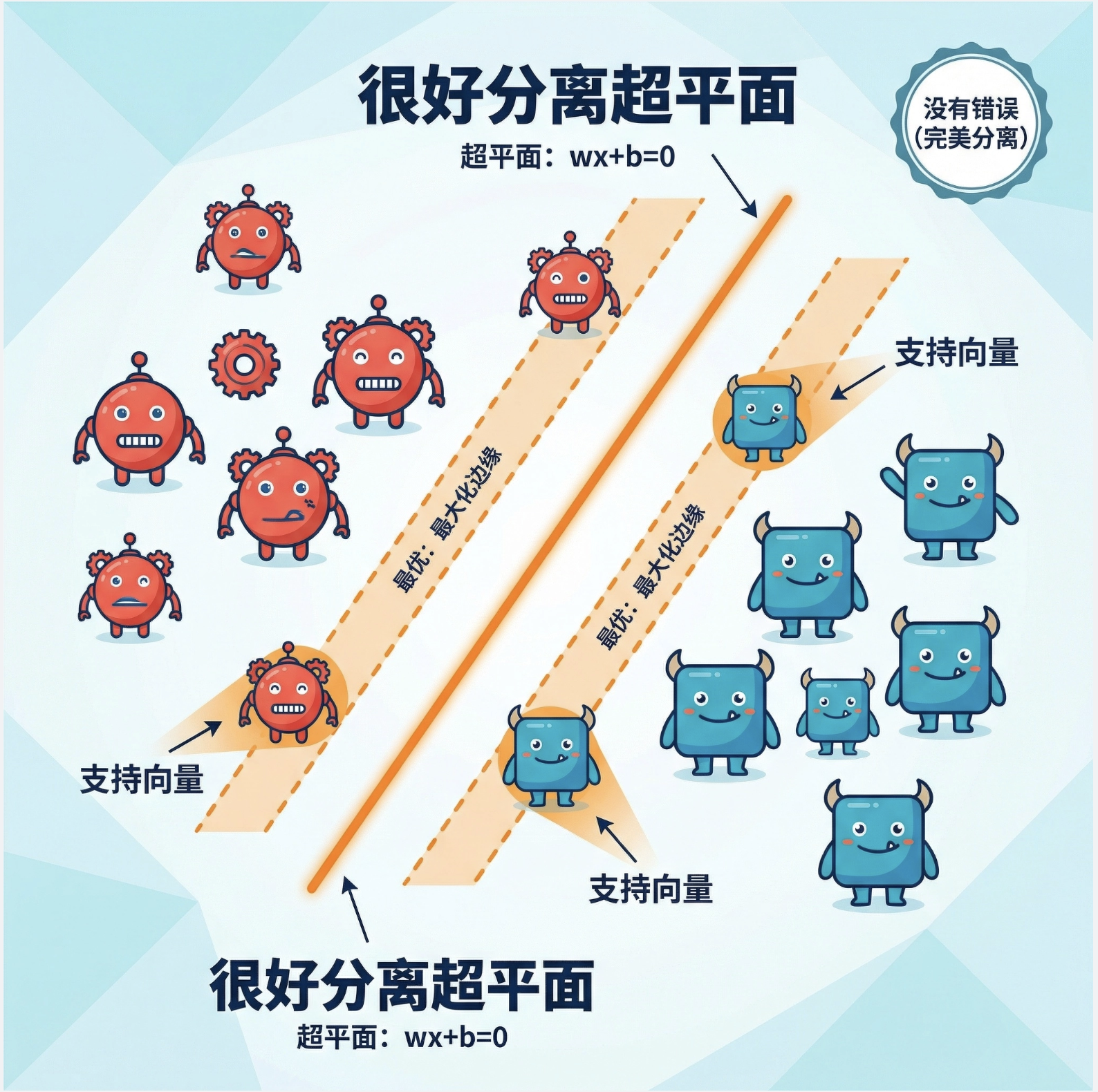
核心概念
“很好分离超平面” 就是线性可分数据的最优分界线:
- 超平面:二维是直线,三维是平面,高维是超平面(公式简化理解:wx+b=0)
- 最优:这个超平面到两类数据的 “最小距离”(边缘)最大(最大化边缘)
- 很好分离:数据完全能被这个超平面分开,没有错误
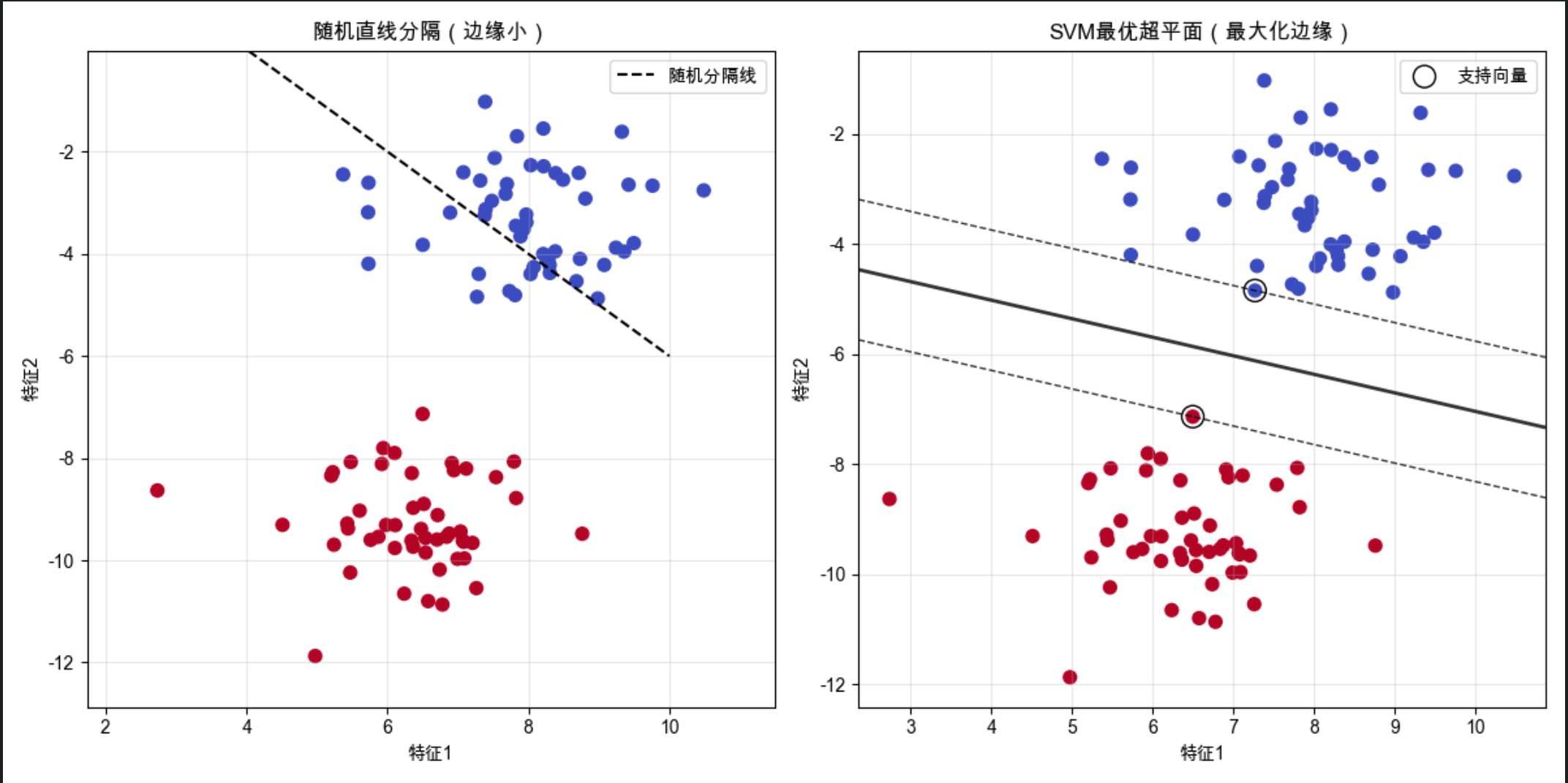
可视化对比:随机直线 vs SVM 最优超平面
下面用代码生成线性可分数据,对比 “随便画的直线” 和 “SVM 最优超平面” 的效果,直观理解 “最优” 的含义:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs
# ========== Mac系统Matplotlib中文显示配置 ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成线性可分的模拟数据
X, y = make_blobs(n_samples=100, centers=2, random_state=6, cluster_std=1.0)
# 2. 训练线性SVM(很好分离超平面)
svm_model = SVC(kernel='linear', C=1000) # C很大表示硬边缘,不允许错误
svm_model.fit(X, y)
# 3. 绘制图形(同一个窗口显示对比)
plt.figure(figsize=(12, 6))
# 子图1:随机直线(非最优)
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm')
# 随便画一条分隔直线(y = -x + 4)
x_random = np.linspace(-10, 10, 100)
y_random = -x_random + 4
plt.plot(x_random, y_random, 'k--', label='随机分隔线')
plt.xlim(X[:, 0].min()-1, X[:, 0].max()+1)
plt.ylim(X[:, 1].min()-1, X[:, 1].max()+1)
plt.title('随机直线分隔(边缘小)', fontsize=12)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)
# 子图2:SVM最优超平面(很好分离)
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm')
# 绘制SVM超平面和边缘
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# 生成网格点用于绘制决策边界
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svm_model.decision_function(xy).reshape(XX.shape)
# 绘制决策边界和边缘
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.8,
linestyles=['--', '-', '--'], linewidths=[1, 2, 1])
# 标记支持向量
ax.scatter(svm_model.support_vectors_[:, 0], svm_model.support_vectors_[:, 1],
s=150, linewidth=1, facecolors='none', edgecolors='k', label='支持向量')
plt.title('SVM最优超平面(最大化边缘)', fontsize=12)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
代码解释
make_blobs:生成 2 类线性可分的模拟数据,方便可视化SVC(kernel='linear', C=1000):线性核 SVM,C 很大表示 “硬边缘”(不允许分类错误)- 决策边界绘制:通过
decision_function计算每个点到超平面的距离,绘制出超平面(中间实线)和边缘(两侧虚线) - 支持向量:用空心圆标记,这些是决定超平面位置的关键数据点
运行效果
- 左图:随机直线虽然能分开数据,但边缘很小,对新数据的泛化能力差
- 右图:SVM 超平面最大化了边缘,支持向量是离超平面最近的点,超平面的位置完全由这些点决定
13.3 不可分情况:软边缘超平面
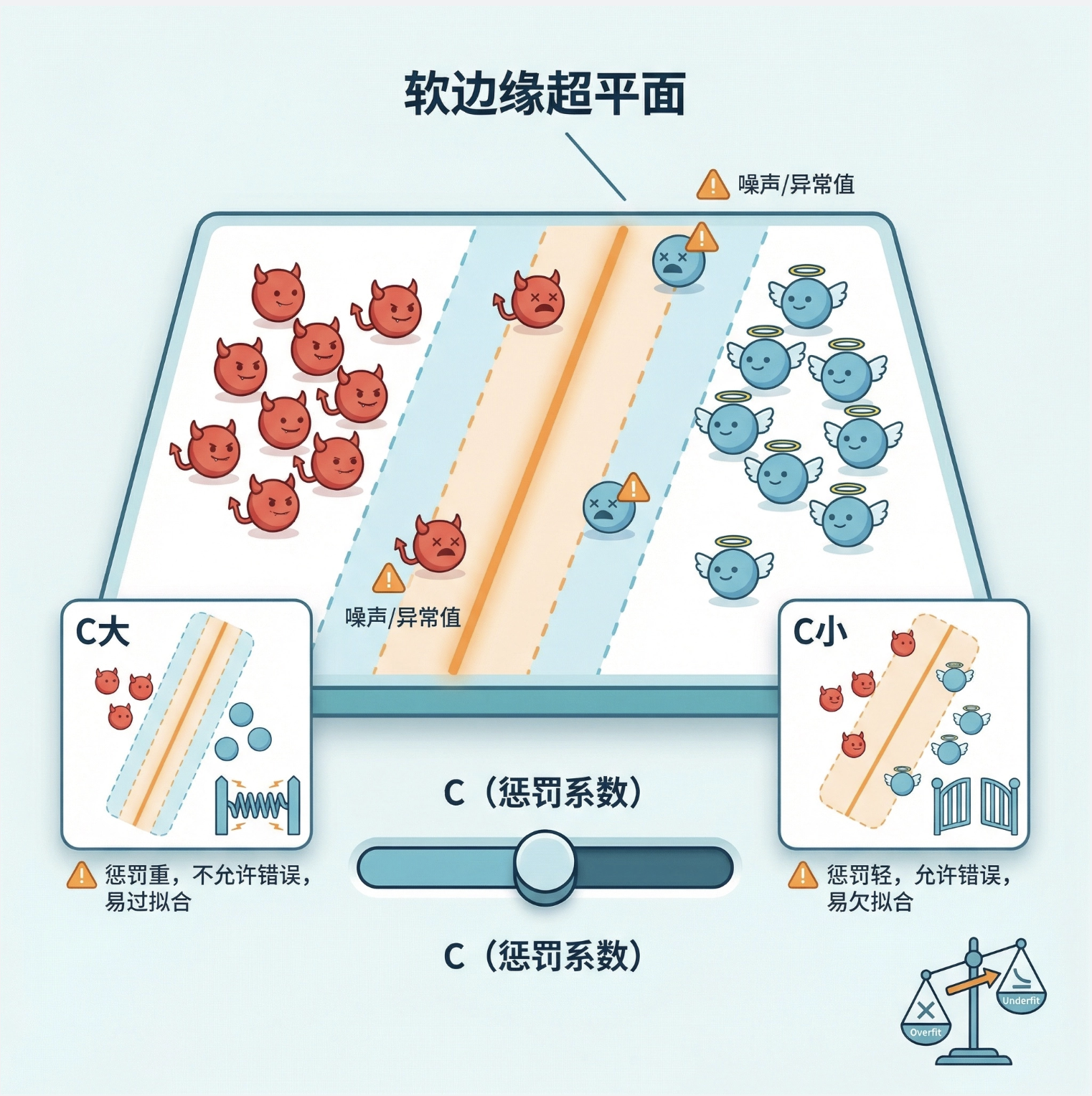
核心概念
现实中数据很少完全线性可分(比如有噪声、异常值),“软边缘超平面” 就是允许少量数据点越过边缘甚至分类错误,来换取对整体数据更好的泛化能力。
关键参数:C(惩罚系数)
C越大:惩罚越重,不允许太多错误(接近硬边缘),容易过拟合C越小:惩罚越轻,允许更多错误(边缘更 “软”),容易欠拟合
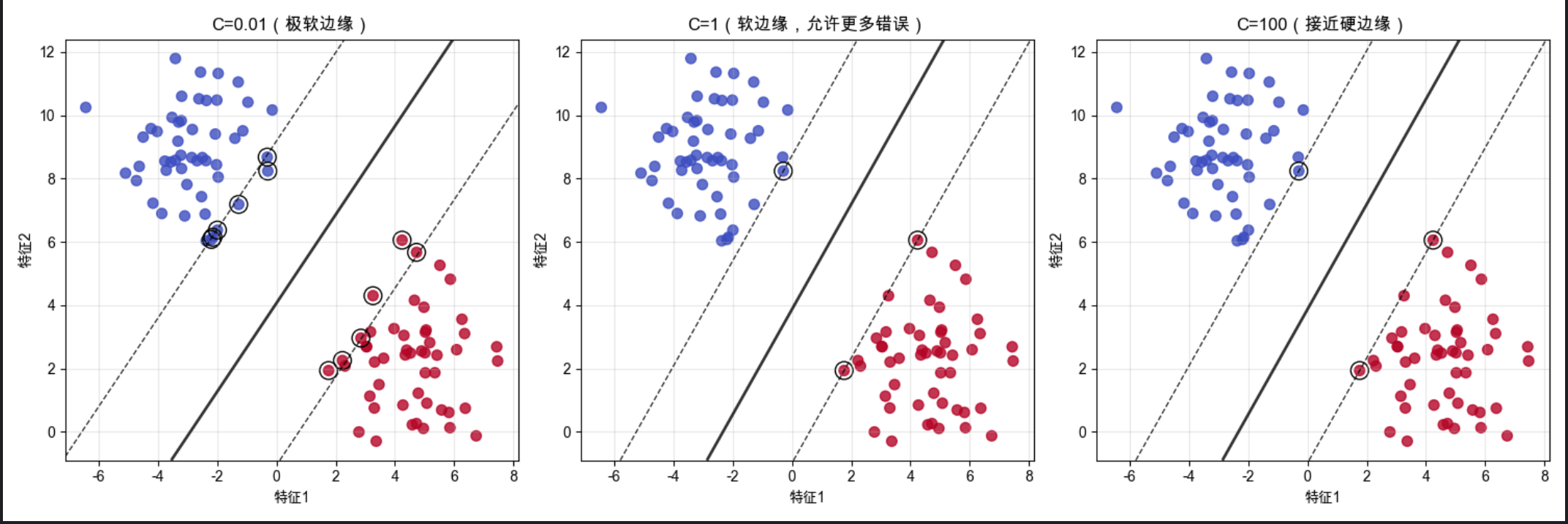
可视化对比:不同 C 值的软边缘效果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs
# Mac字体配置(同上)
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成带噪声的线性不可分数据
X, y = make_blobs(n_samples=100, centers=2, random_state=42, cluster_std=1.5)
# 2. 定义不同C值的SVM模型
C_values = [0.01, 1, 100]
models = [SVC(kernel='linear', C=c).fit(X, y) for c in C_values]
# 3. 绘制对比图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
titles = [f'C={c}(软边缘,允许更多错误)' for c in C_values]
titles[0] = 'C=0.01(极软边缘)'
titles[2] = 'C=100(接近硬边缘)'
for ax, model, title in zip(axes, models, titles):
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
# 绘制决策边界和边缘
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.8,
linestyles=['--', '-', '--'], linewidths=[1, 2, 1])
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],
s=150, linewidth=1, facecolors='none', edgecolors='k')
ax.set_title(title, fontsize=12)
ax.set_xlabel('特征1')
ax.set_ylabel('特征2')
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()
代码解释
1.生成带噪声的数据集(cluster_std=1.5 增大数据分散度,制造不可分场景)
2.对比 3 个不同 C 值的 SVM:C=0.01:极软边缘,允许很多数据点在边缘内,甚至分类错误;C=1:平衡的软边缘,兼顾拟合和泛化;C=100:接近硬边缘,几乎不允许错误,对噪声敏感
运行效果
- C 越小,边缘越 “宽”,允许更多异常值,泛化能力更强
- C 越大,边缘越 “窄”,对训练数据拟合越好,但容易过拟合
13.4 ν-SVM
核心概念
ν-SVM 是对软边缘 SVM 的改进,用参数ν替代C,ν有更直观的物理意义:
ν取值范围:(0, 1]- 含义:
ν同时控制 “支持向量的比例” 和 “允许错误分类的样本比例”,比如ν=0.1表示:- 至少 10% 的样本是支持向量
- 最多 10% 的样本被错误分类
简单说:ν 是 “容错率” 的直接体现,比C更容易调参。
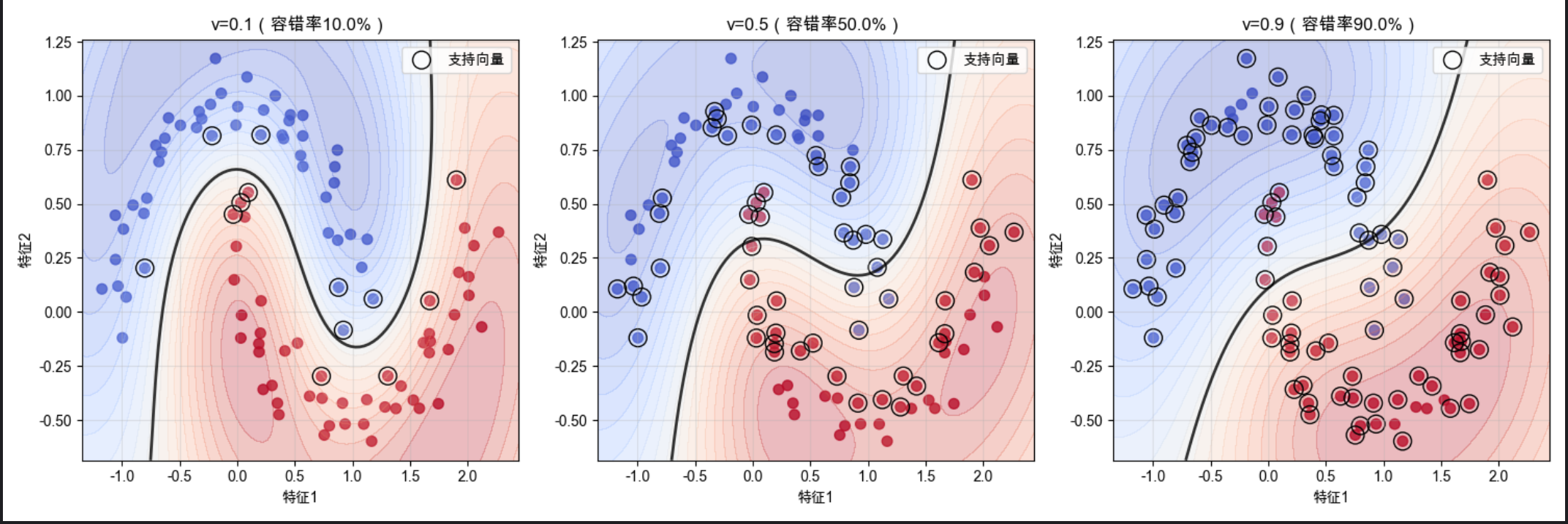
可视化对比:不同 ν 值的效果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVC # 替换为NuSVC(ν-SVM专用类)
from sklearn.datasets import make_moons
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成非线性数据(月亮形数据)
X, y = make_moons(n_samples=100, noise=0.1, random_state=42)
# 2. 定义不同ν值的ν-SVM模型(用RBF核)
nu_values = [0.1, 0.5, 0.9]
# 关键修改:用NuSVC替代SVC,参数nu有效
models = [NuSVC(kernel='rbf', nu=nu, gamma='scale').fit(X, y) for nu in nu_values]
# 3. 绘制对比图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
titles = [f'ν={nu}(容错率{nu * 100}%)' for nu in nu_values]
for ax, model, title in zip(axes, models, titles):
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
# 绘制决策边界
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 100)
yy = np.linspace(ylim[0], ylim[1], 100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
ax.contourf(XX, YY, Z, levels=np.linspace(Z.min(), Z.max(), 20), alpha=0.3, cmap='coolwarm')
ax.contour(XX, YY, Z, colors='k', levels=[0], alpha=0.8, linewidths=2)
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],
s=150, linewidth=1, facecolors='none', edgecolors='k', label='支持向量')
ax.set_title(title, fontsize=12)
ax.set_xlabel('特征1')
ax.set_ylabel('特征2')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
make_moons:生成非线性的月亮形数据,模拟真实场景的不可分数据SVC(kernel='rbf', nu=nu):ν-SVM,用 RBF 核(径向基核,后续讲解)contourf:绘制决策边界的颜色填充,更直观看到分类区域
运行效果
- ν=0.1:容错率 10%,支持向量少,决策边界简洁,泛化能力强
- ν=0.5:容错率 50%,支持向量多,决策边界更贴合数据
- ν=0.9:容错率 90%,几乎所有样本都是支持向量,决策边界过拟合
13.5 核技巧(核心中的核心)

核心概念
核技巧是核机器的 “灵魂”,可以用一句大白话解释:
不直接把数据映射到高维空间,而是通过 “核函数” 直接计算高维空间的内积,既达到高维线性可分的效果,又避免了高维计算的复杂度。
打个比方:
- 低维空间:你在地面上看一堆缠绕的绳子(线性不可分)
- 高维空间:你飞到空中看,绳子其实是分层的(线性可分)
- 核技巧:不用真的 “飞起来”(映射高维),而是通过 “望远镜”(核函数)直接看到分层的效果
常见核函数:
| 核函数 | 适用场景 |
|---|---|
| 线性核(linear) | 数据本身线性可分 |
| 多项式核(poly) | 数据有多项式分布规律 |
| 径向基核(rbf) | 大多数非线性场景(万能核) |
| 西格玛核(sigmoid) | 模拟神经网络 |
可视化对比:不同核函数的效果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_circles
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成环形非线性数据(低维完全不可分)
X, y = make_circles(n_samples=200, noise=0.1, factor=0.2, random_state=42)
# 2. 定义不同核函数的SVM模型
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
models = [SVC(kernel=k, gamma='scale').fit(X, y) for k in kernels]
# 3. 绘制对比图
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.flatten()
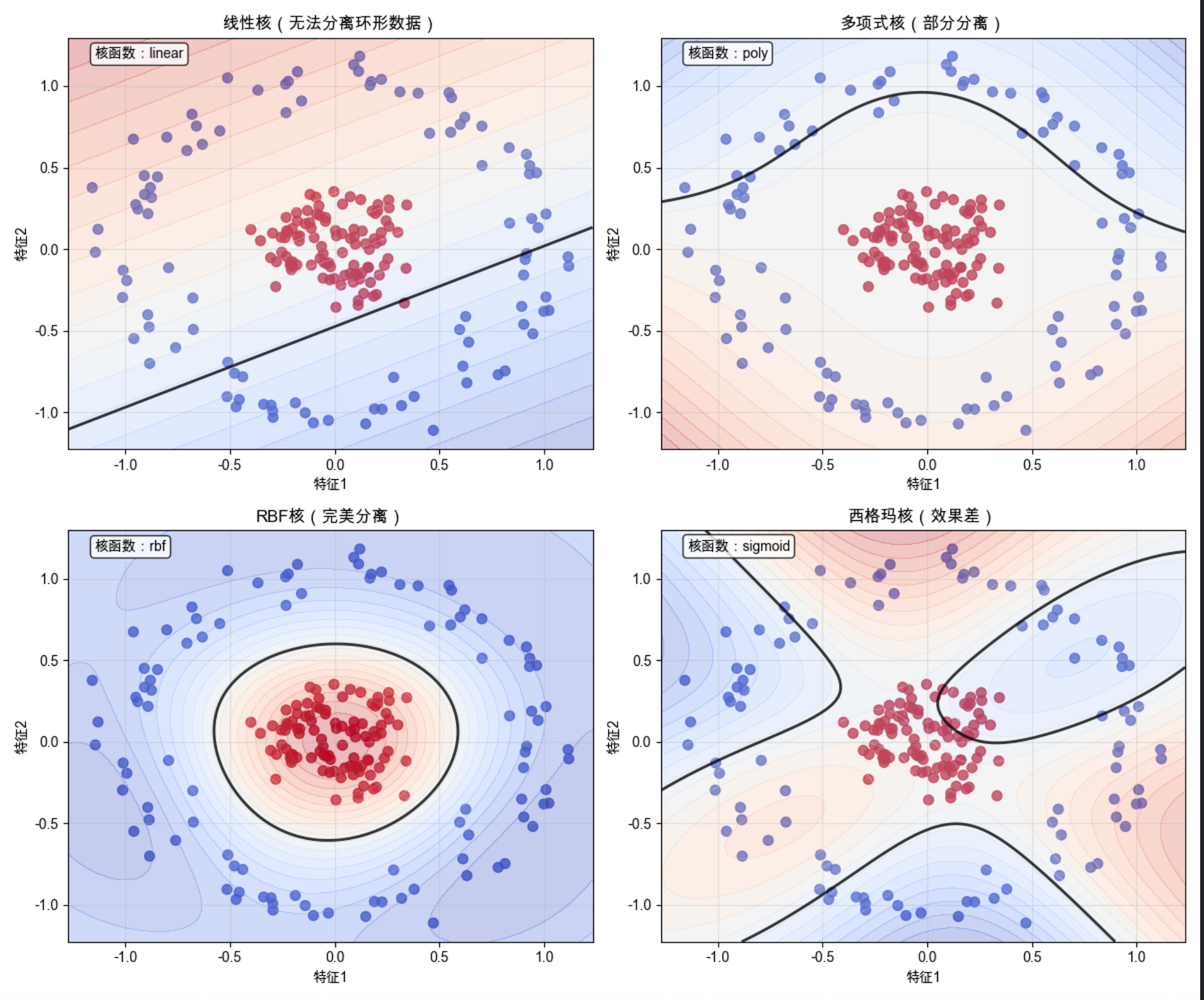
titles = ['线性核(无法分离环形数据)', '多项式核(部分分离)', 'RBF核(完美分离)', '西格玛核(效果差)']
for ax, model, title, kernel in zip(axes, models, titles, kernels):
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
# 绘制决策边界
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 100)
yy = np.linspace(ylim[0], ylim[1], 100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
ax.contourf(XX, YY, Z, levels=np.linspace(Z.min(), Z.max(), 20), alpha=0.3, cmap='coolwarm')
ax.contour(XX, YY, Z, colors='k', levels=[0], alpha=0.8, linewidths=2)
ax.set_title(title, fontsize=12)
ax.set_xlabel('特征1')
ax.set_ylabel('特征2')
ax.grid(alpha=0.3)
# 标注核函数名称
ax.text(0.05, 0.95, f'核函数:{kernel}', transform=ax.transAxes,
bbox=dict(boxstyle='round', facecolor='white', alpha=0.8), fontsize=10)
plt.tight_layout()
plt.show()
代码解释
1.make_circles:生成环形数据(低维线性完全不可分,必须用核技巧)
2.对比 4 种核函数:线性核:无法分离环形数据(决策边界还是直线);多项式核:能分离部分,但效果差;RBF 核:完美分离环形数据(决策边界是环形);西格玛核:效果差,不适合环形数据
运行效果
核技巧的核心价值:RBF 核把低维不可分的环形数据,通过 “隐式高维映射” 变成可分,而线性核做不到
选择合适的核函数是核机器的关键(RBF 核是通用选择)
13.6 向量核
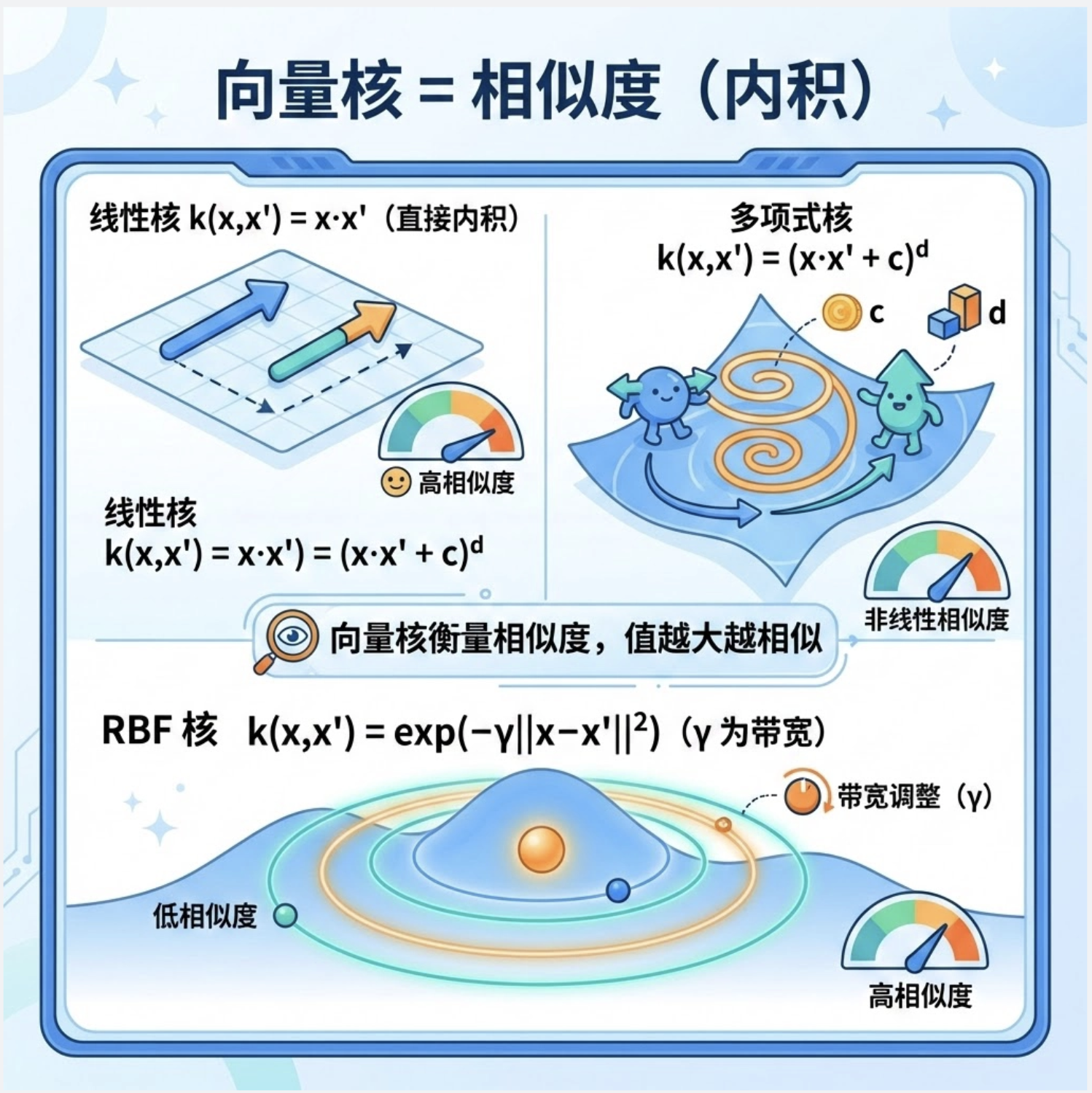
核心概念
向量核是核函数的 “基础形态”,本质是两个向量在高维空间的内积。比如:
- 线性核:k(x,x′)=x⋅x′(直接计算低维内积)
- 多项式核:k(x,x′)=(x⋅x′+c)d(c 是常数,d 是多项式次数)
- RBF 核:k(x,x′)=exp(−γ∣∣x−x′∣∣2)(γ 是带宽参数)
你可以把向量核理解成:衡量两个向量的 “相似度”,值越大,相似度越高。
代码:向量核的相似度计算
import numpy as np
# 定义向量核函数
def linear_kernel(x1, x2):
"""线性核:直接内积"""
return np.dot(x1, x2)
def polynomial_kernel(x1, x2, degree=2, coef0=1):
"""多项式核"""
return (np.dot(x1, x2) + coef0) ** degree
def rbf_kernel(x1, x2, gamma=0.1):
"""RBF核:径向基核"""
return np.exp(-gamma * np.linalg.norm(x1 - x2) ** 2)
# 测试向量
x1 = np.array([1, 2])
x2 = np.array([3, 4])
x3 = np.array([1.1, 2.1]) # 和x1高度相似
# 计算相似度
print("=== 向量核相似度计算 ===")
print(f"x1 = {x1}, x2 = {x2}, x3 = {x3}")
print(f"线性核 - x1&x2: {linear_kernel(x1, x2):.2f}, x1&x3: {linear_kernel(x1, x3):.2f}")
print(f"多项式核 - x1&x2: {polynomial_kernel(x1, x2):.2f}, x1&x3: {polynomial_kernel(x1, x3):.2f}")
print(f"RBF核 - x1&x2: {rbf_kernel(x1, x2):.2f}, x1&x3: {rbf_kernel(x1, x3):.2f}")
# 可视化RBF核的相似度(2D热力图)
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成网格点
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
# 计算每个点到x1的RBF核相似度
center = x1
for i in range(len(x)):
for j in range(len(y)):
point = np.array([X[i,j], Y[i,j]])
Z[i,j] = rbf_kernel(center, point, gamma=0.5)
# 绘制热力图
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=20, cmap='viridis')
plt.colorbar(label='RBF核相似度')
plt.scatter(center[0], center[1], c='red', s=200, marker='*', label='中心向量x1')
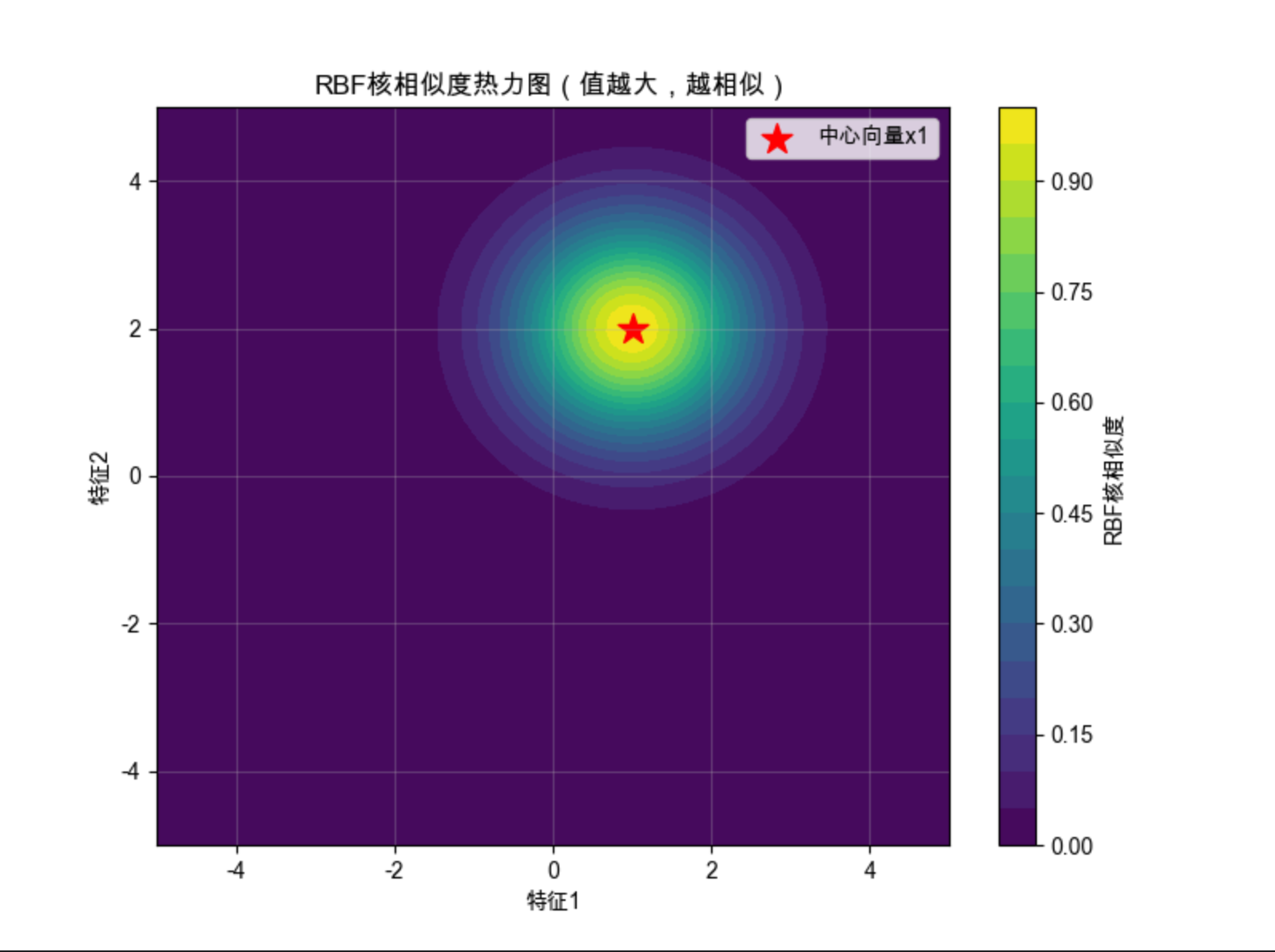
plt.title('RBF核相似度热力图(值越大,越相似)', fontsize=12)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)
plt.show()
代码解释
- 手动实现 3 种向量核函数,直观理解核函数的计算逻辑
- 相似度测试:x3 和 x1 相似,所以核函数值更大
- 热力图:RBF 核的相似度是 “以中心向量为圆心的同心圆”,离中心越近,相似度越高
运行效果
- 向量核的本质是 “相似度度量”,RBF 核的相似度随距离增加呈指数衰减
- 这也是 RBF 核能处理非线性数据的原因:通过相似度把数据分成不同的 “簇”
13.7 定义核
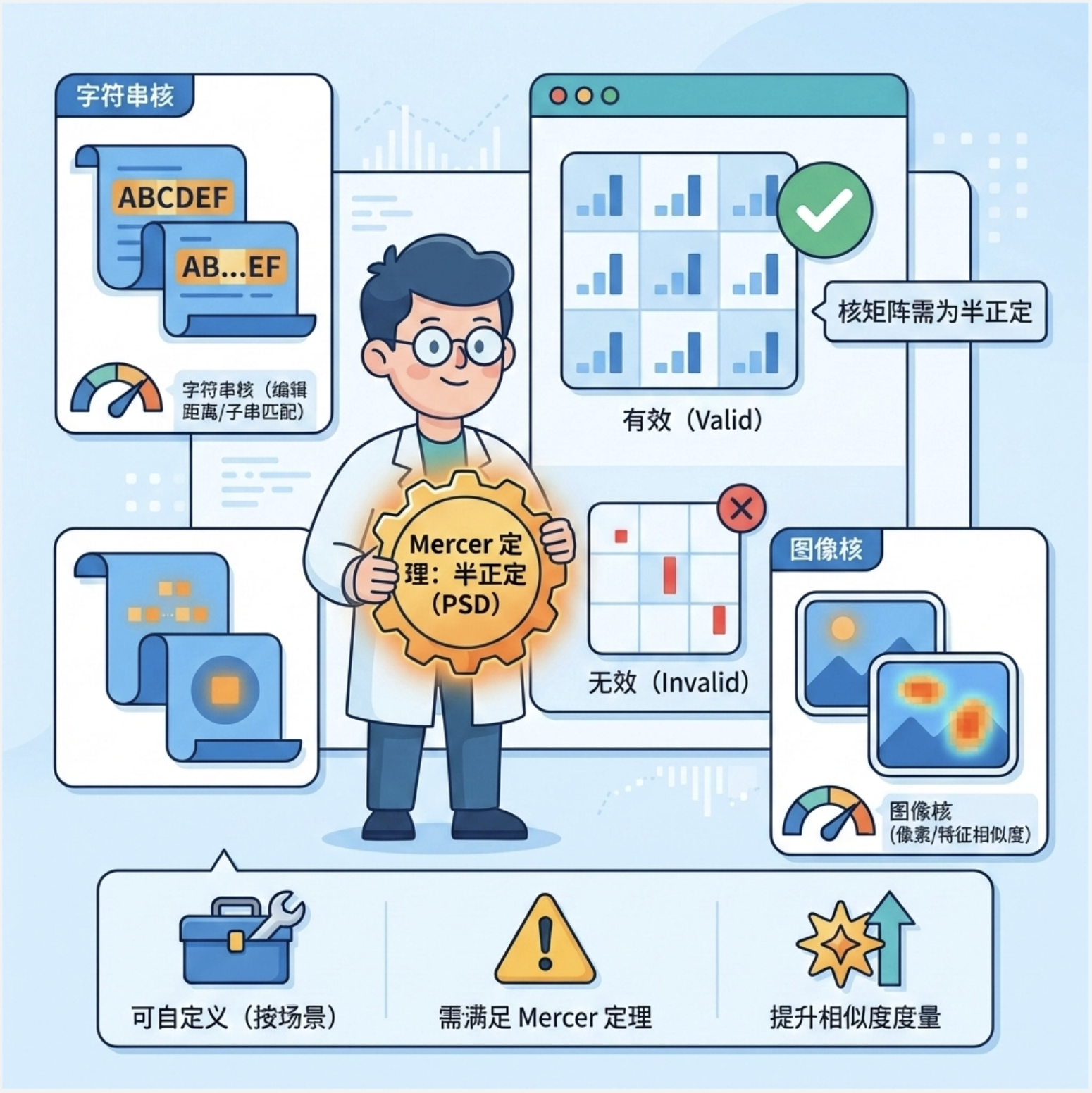
核心概念
自定义核函数的核心原则:必须满足 Mercer 定理(简单说:核矩阵必须是半正定的)。你可以根据业务场景自定义核,比如:
- 字符串核:处理文本数据(比如计算两个字符串的编辑距离)
- 图像核:处理图像数据(比如计算两个图像的像素相似度)
代码:自定义核函数(字符串核 + 图像核)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.metrics.pairwise import pairwise_kernels, euclidean_distances
from sklearn.datasets import make_classification
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 自定义字符串核(简化版:字符匹配数 / 总长度)
def string_kernel(s1, s2):
"""自定义字符串核:计算两个字符串的相似度"""
min_len = min(len(s1), len(s2))
match = sum(1 for i in range(min_len) if s1[i] == s2[i])
return match / max(len(s1), len(s2))
# 测试字符串核
s1 = "hello world"
s2 = "hello python"
s3 = "hi world"
print("=== 自定义字符串核 ===")
print(f"相似度(s1,s2) = {string_kernel(s1, s2):.2f}")
print(f"相似度(s1,s3) = {string_kernel(s1, s3):.2f}")
# 2. 自定义图像核(简化版:像素差值的负平方)
def image_kernel(img1, img2, gamma=0.1): # 增大gamma,体现相似度差异
"""自定义图像核:输入是扁平化的图像像素数组"""
return np.exp(-gamma * np.sum((img1 - img2) ** 2))
# 生成模拟图像数据(28x28简化成5x5)
np.random.seed(42) # 固定随机种子,结果可复现
img1 = np.random.rand(25) # 图像1
img2 = np.random.rand(25) # 图像2
img3 = img1 + 0.01 * np.random.rand(25) # 图像1的轻微噪声版
print("\n=== 自定义图像核 ===")
print(f"相似度(img1,img2) = {image_kernel(img1, img2):.2f}")
print(f"相似度(img1,img3) = {image_kernel(img1, img3):.2f}")
# 3. 在SVM中使用自定义核
# 生成分类数据
X, y = make_classification(n_samples=100, n_features=10, n_informative=5, random_state=42)
# 自定义核函数(基于欧氏距离的核)
def custom_kernel(X1, X2):
"""自定义核:exp(-gamma * 欧氏距离的平方)
修正点:
1. 用euclidean_distances计算欧氏距离(专门的距离函数)
2. 对距离平方做核变换,符合RBF核的形式
"""
gamma = 0.1
# 第一步:计算欧氏距离矩阵
dist = euclidean_distances(X1, X2)
# 第二步:转换为核矩阵(RBF核形式)
kernel = np.exp(-gamma * (dist ** 2))
return kernel
# 训练SVM
svm_custom = SVC(kernel=custom_kernel)
svm_custom.fit(X, y)
# 测试准确率
accuracy = svm_custom.score(X, y)
print("\n=== 自定义核SVM ===")
print(f"训练集准确率:{accuracy:.2f}")
# 可视化自定义核的核矩阵
kernel_matrix = custom_kernel(X, X)
plt.figure(figsize=(8, 6))
plt.imshow(kernel_matrix, cmap='viridis')
plt.colorbar(label='核矩阵值(相似度)')
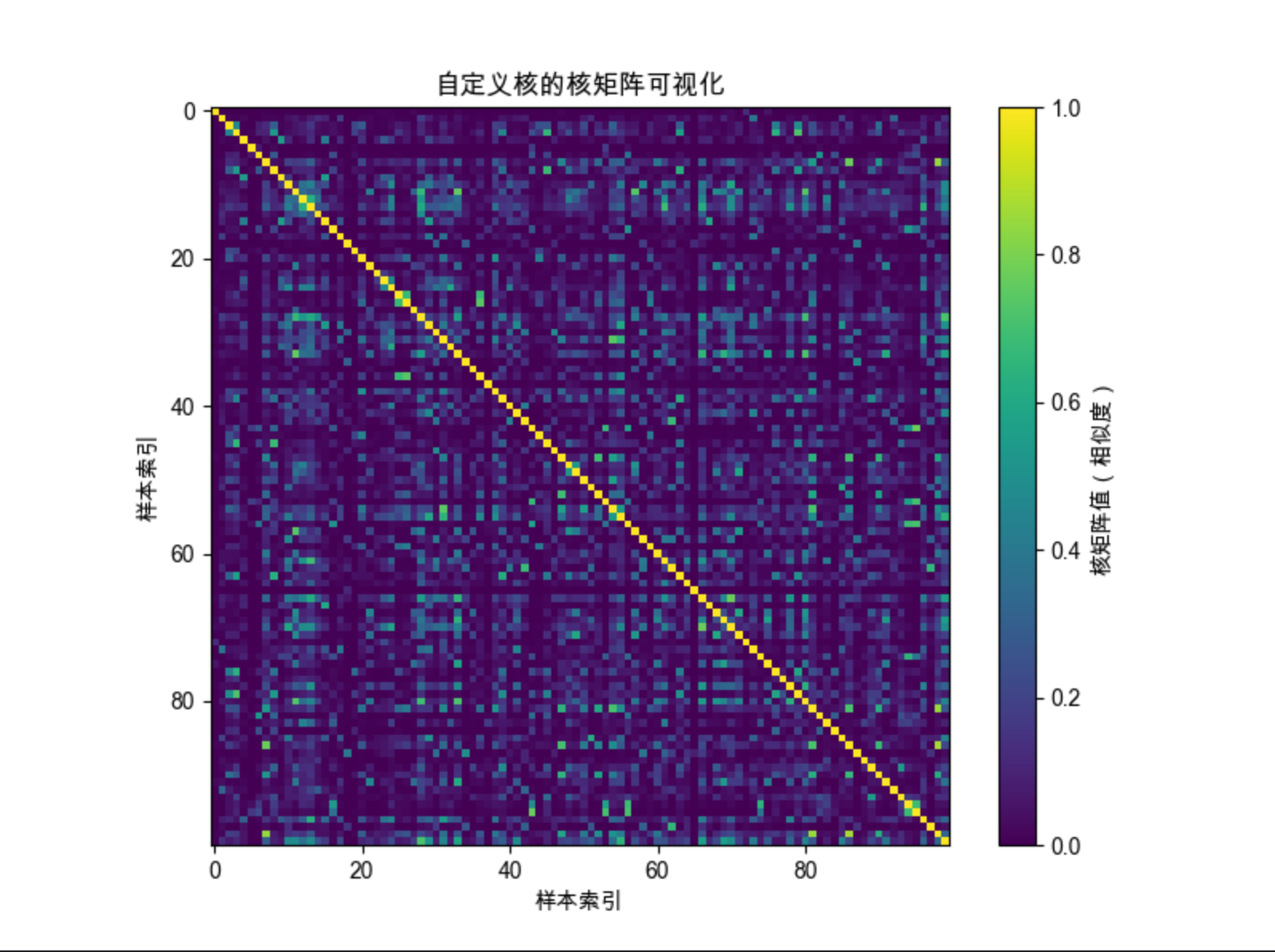
plt.title('自定义核的核矩阵可视化', fontsize=12)
plt.xlabel('样本索引')
plt.ylabel('样本索引')
plt.show()代码解释
- 字符串核:通过字符匹配数计算相似度,适合文本分类
- 图像核:通过像素差值计算相似度,适合图像分类
- 在 SVM 中使用自定义核:需要把核函数传入
SVC(kernel=自定义函数) - 核矩阵可视化:对角线是样本自身的相似度(值最大),越靠近对角线,相似度越高
运行效果
- 自定义核可以适配特定业务场景(文本、图像等)
- 核矩阵是对称矩阵,半正定(满足 Mercer 定理)
13.8 多核学习

核心概念
多核学习是 “不要把鸡蛋放在一个篮子里”——组合多个不同的核函数,取各自的优点,提升模型性能。比如:
- 组合线性核 + RBF 核:兼顾线性拟合和非线性拟合
- 组合多项式核 + RBF 核:兼顾局部和全局特征
代码:多核学习实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_moons
from sklearn.ensemble import VotingClassifier
from sklearn.metrics import accuracy_score
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成数据
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
X_train, X_test = X[:150], X[150:]
y_train, y_test = y[:150], y[150:]
# 2. 定义多个核的SVM模型
svm_linear = SVC(kernel='linear', probability=True, random_state=42)
svm_poly = SVC(kernel='poly', degree=3, probability=True, random_state=42)
svm_rbf = SVC(kernel='rbf', gamma='scale', probability=True, random_state=42)
# 3. 多核融合(投票法)
multi_kernel_svm = VotingClassifier(
estimators=[
('linear', svm_linear),
('poly', svm_poly),
('rbf', svm_rbf)
],
voting='soft', # 软投票:基于概率加权
weights=[1, 1, 2] # RBF核权重更高
)
# 4. 训练和评估
# 单个核模型评估
svm_linear.fit(X_train, y_train)
svm_poly.fit(X_train, y_train)
svm_rbf.fit(X_train, y_train)
multi_kernel_svm.fit(X_train, y_train)
acc_linear = accuracy_score(y_test, svm_linear.predict(X_test))
acc_poly = accuracy_score(y_test, svm_poly.predict(X_test))
acc_rbf = accuracy_score(y_test, svm_rbf.predict(X_test))
acc_multi = accuracy_score(y_test, multi_kernel_svm.predict(X_test))
# 打印结果
print("=== 多核学习效果对比 ===")
print(f"线性核准确率:{acc_linear:.2f}")
print(f"多项式核准确率:{acc_poly:.2f}")
print(f"RBF核准确率:{acc_rbf:.2f}")
print(f"多核融合准确率:{acc_multi:.2f}")
# 5. 可视化决策边界
plt.figure(figsize=(10, 8))
# 绘制每个模型的决策边界
models = [
(svm_linear, '线性核'),
(svm_poly, '多项式核'),
(svm_rbf, 'RBF核'),
(multi_kernel_svm, '多核融合')
]
for i, (model, title) in enumerate(models):
plt.subplot(2, 2, i+1)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()
xx = np.linspace(xlim[0], xlim[1], 100)
yy = np.linspace(ylim[0], ylim[1], 100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.predict_proba(xy)[:, 1].reshape(XX.shape)
plt.contourf(XX, YY, Z, levels=np.linspace(0, 1, 20), alpha=0.3, cmap='coolwarm')
plt.contour(XX, YY, Z, colors='k', levels=[0.5], alpha=0.8, linewidths=2)
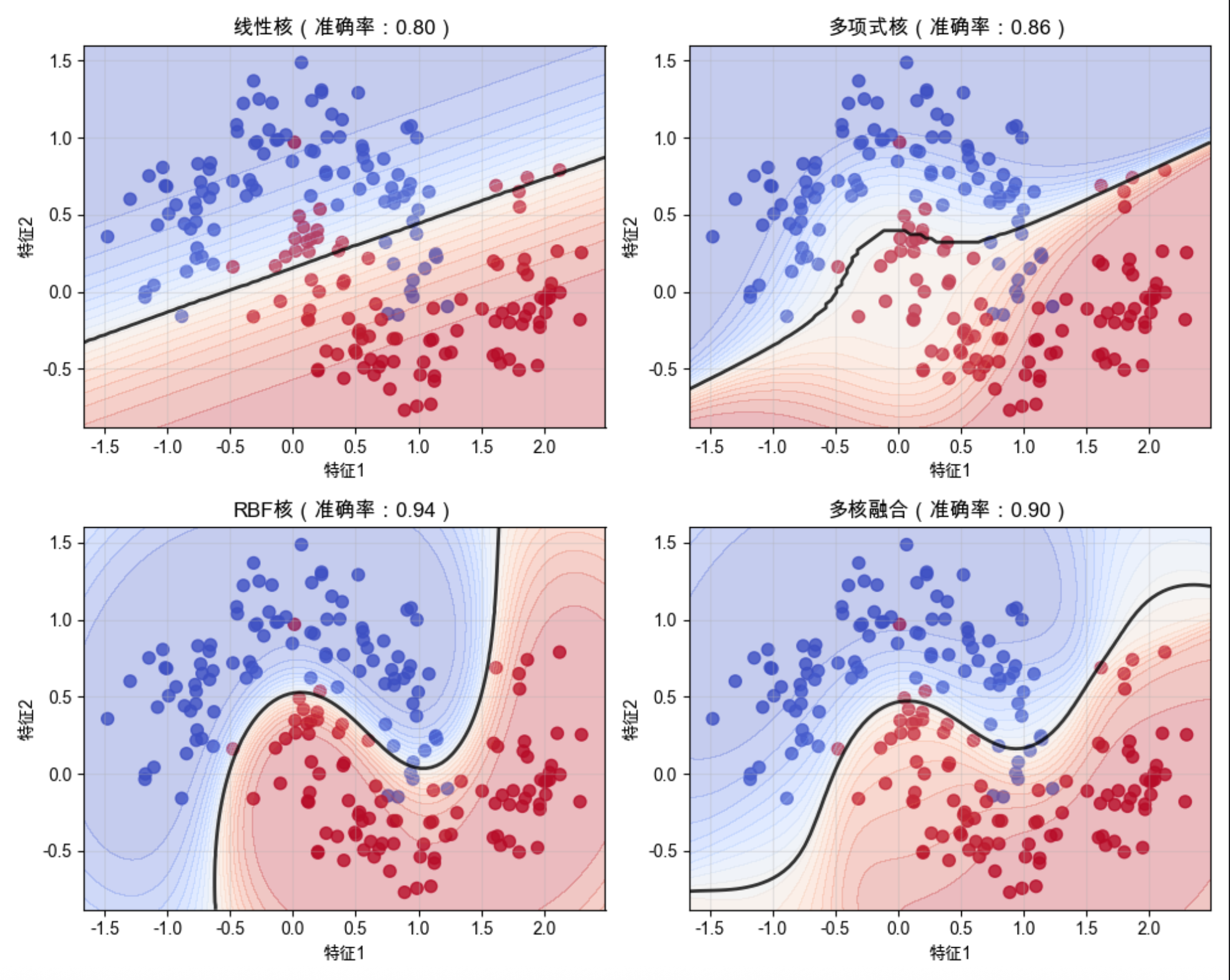
plt.title(f'{title}(准确率:{accuracy_score(y_test, model.predict(X_test)):.2f})', fontsize=12)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
代码解释
- 用
VotingClassifier实现多核融合:组合线性、多项式、RBF 核的 SVM - 软投票:基于每个模型的预测概率加权,权重可以调整(这里给 RBF 核更高权重)
- 对比单个核和多核融合的准确率:多核融合通常能提升性能
运行效果
- 多核学习的准确率通常高于单个核(取长补短)
- 决策边界:多核融合的边界更平滑,泛化能力更强
13.9 多类核机器
核心概念
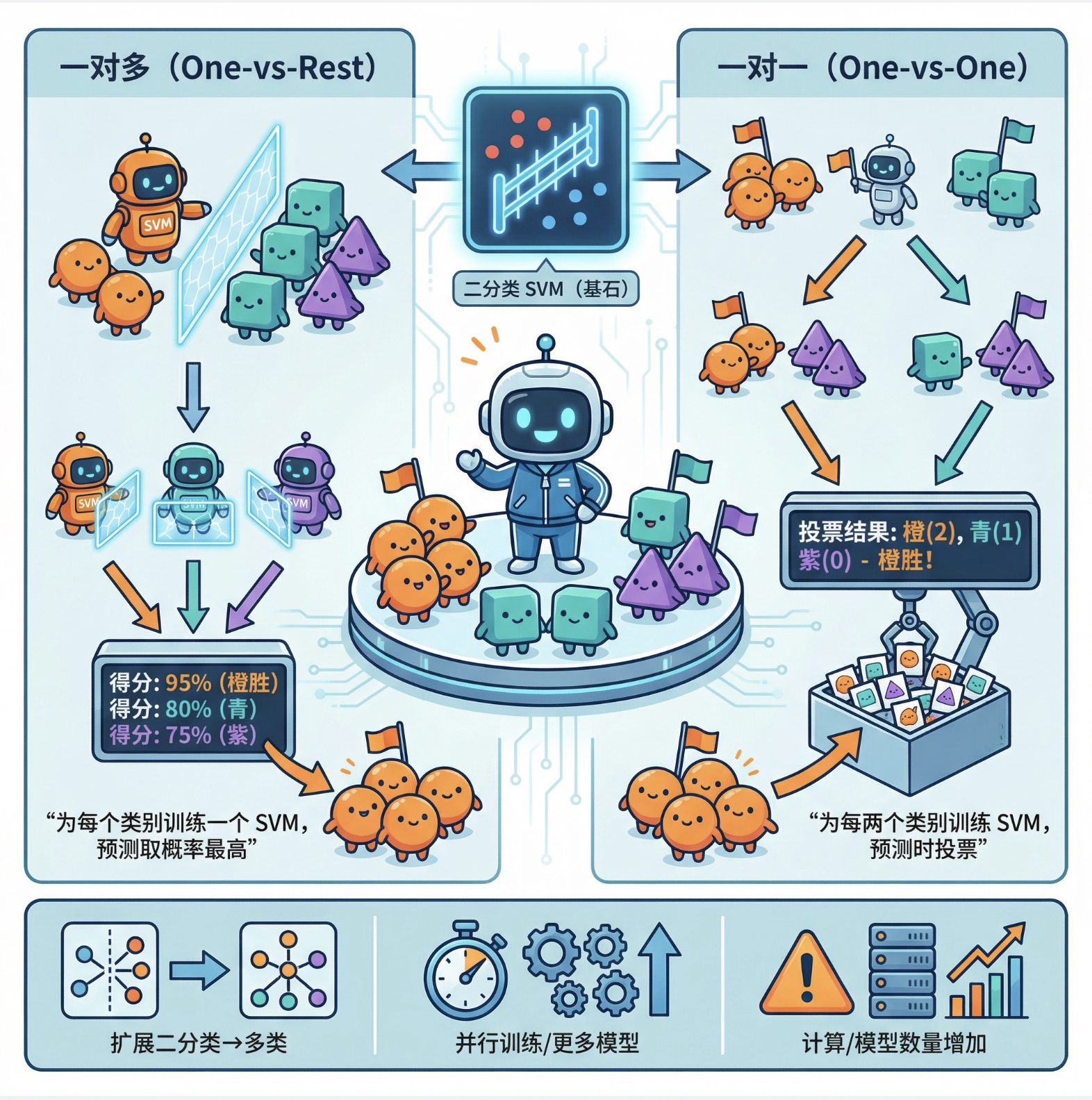
SVM 原本是二分类模型,多类核机器就是把二分类 SVM 扩展到多分类场景,常用方法:
- 一对多(One-vs-Rest):为每个类别训练一个 SVM,预测时选概率最高的类别
- 一对一(One-vs-One):为每两个类别训练一个 SVM,预测时投票
代码:多类核机器实战
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs
from sklearn.metrics import classification_report
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成3类数据
X, y = make_blobs(n_samples=300, centers=3, random_state=42, cluster_std=1.5)
# 2. 训练多类SVM(默认是一对一)
svm_multi = SVC(kernel='rbf', gamma='scale', decision_function_shape='ovo') # ovo=一对一,ovr=一对多
svm_multi.fit(X, y)
# 3. 预测和评估
y_pred = svm_multi.predict(X)
print("=== 多类核机器评估报告 ===")
print(classification_report(y, y_pred))
# 4. 可视化多类决策边界
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='viridis', alpha=0.8)
# 绘制决策边界
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()
xx = np.linspace(xlim[0], xlim[1], 100)
yy = np.linspace(ylim[0], ylim[1], 100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svm_multi.predict(xy).reshape(XX.shape)
plt.contourf(XX, YY, Z, levels=[-0.5, 0.5, 1.5, 2.5], alpha=0.3, cmap='viridis')
plt.contour(XX, YY, Z, colors='k', levels=[0, 1, 2], alpha=0.8, linewidths=2)
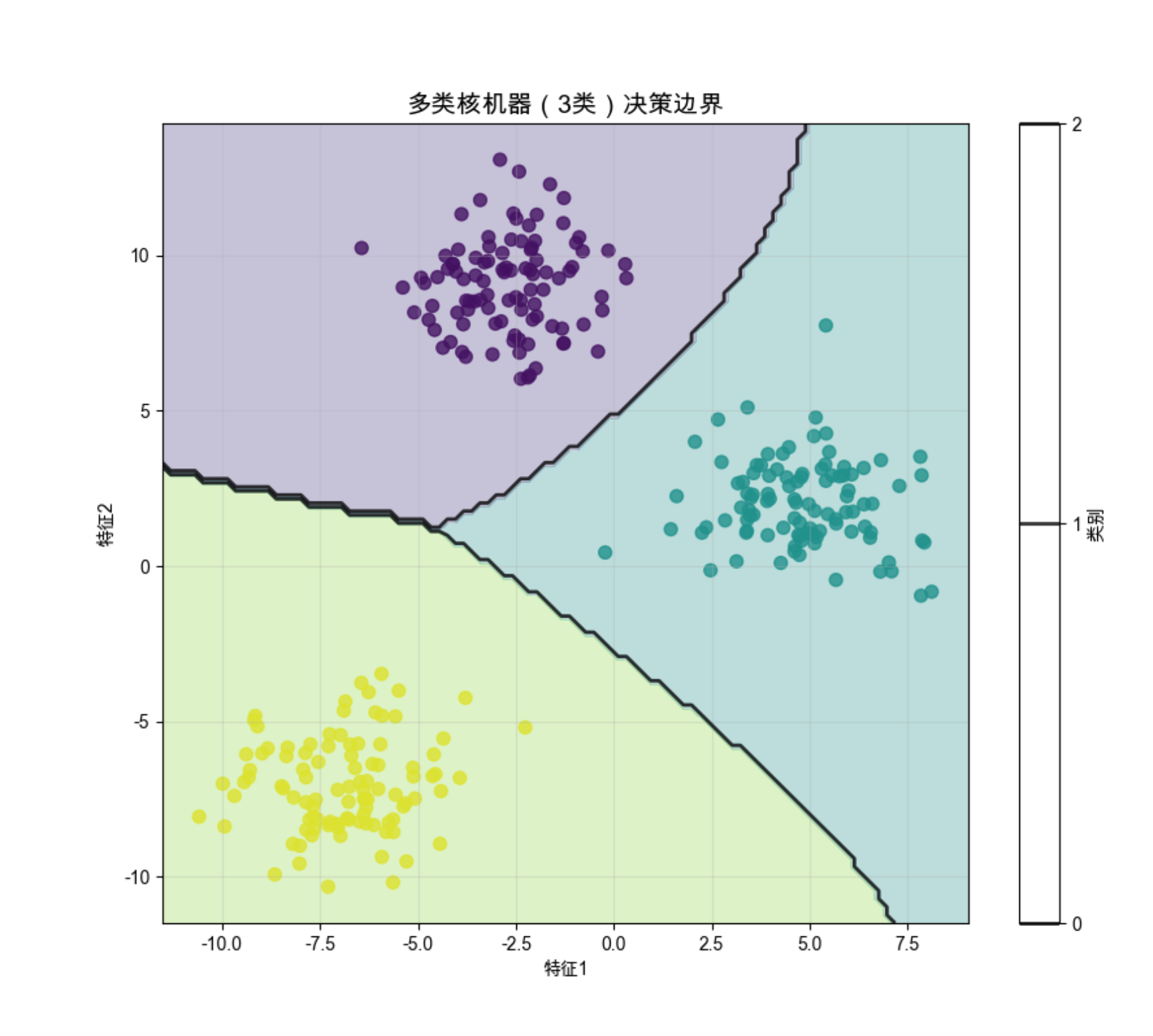
plt.title('多类核机器(3类)决策边界', fontsize=14)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.colorbar(label='类别')
plt.grid(alpha=0.3)
plt.show()
# 5. 对比一对一和一对多
svm_ovr = SVC(kernel='rbf', gamma='scale', decision_function_shape='ovr')
svm_ovr.fit(X, y)
y_pred_ovr = svm_ovr.predict(X)
print("\n=== 一对一 vs 一对多 ===")
print(f"一对一准确率:{np.mean(y_pred == y):.2f}")
print(f"一对多准确率:{np.mean(y_pred_ovr == y):.2f}")
代码解释
decision_function_shape:指定多分类策略(ovo = 一对一,ovr = 一对多)- 一对一:适合类别少的场景(3 类需要训练 3 个 SVM)
- 一对多:适合类别多的场景(3 类需要训练 3 个 SVM,和一对一数量相同;N 类需要训练 N 个)
运行效果
- 多类核机器能很好地处理多分类问题,RBF 核的效果最优
- 一对一和一对多的准确率在简单数据上差别不大,复杂数据上一对一通常更好
13.10 用于回归的核机器(SVR)
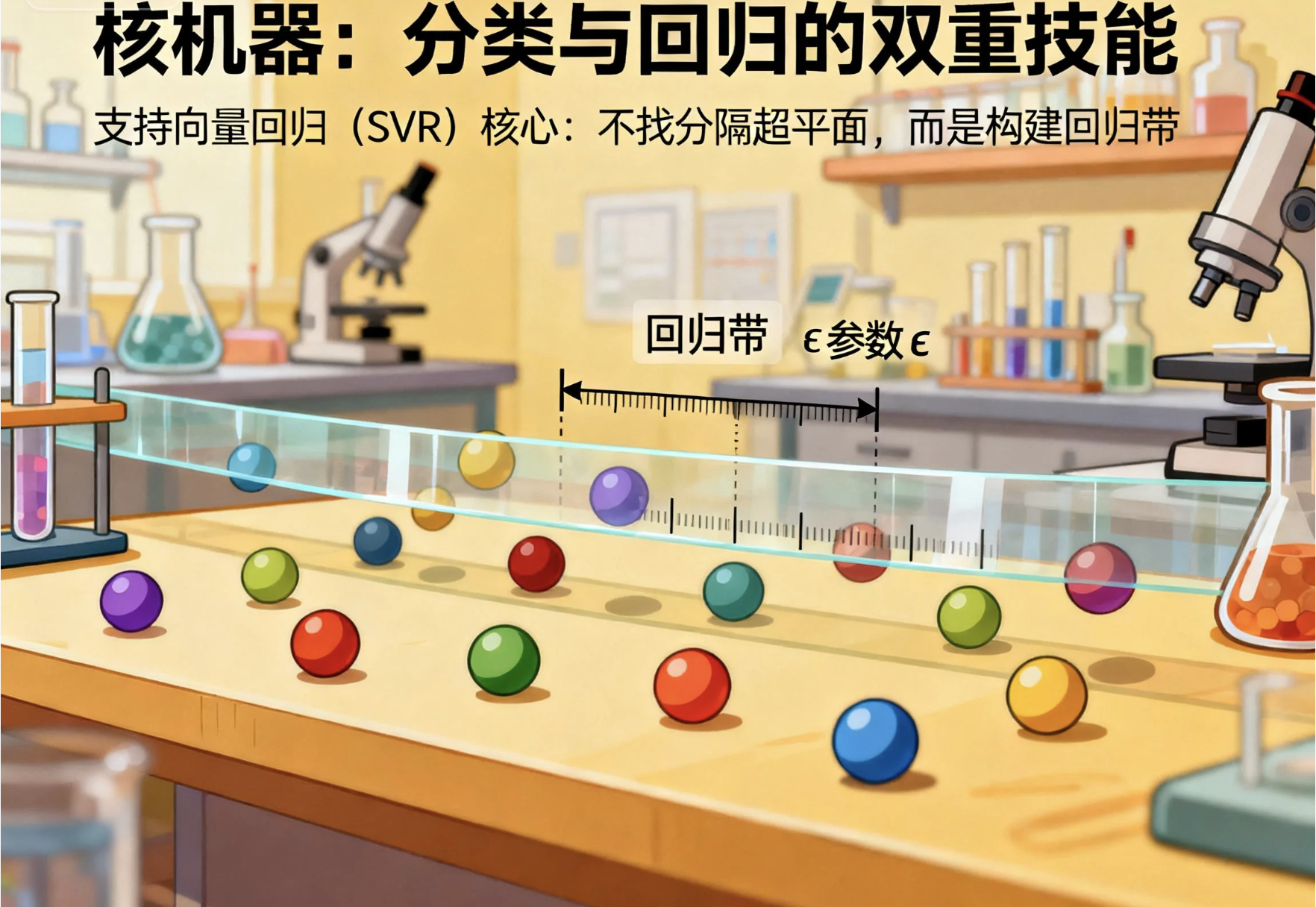
核心概念
核机器不仅能分类,还能做回归(SVR:支持向量回归)。核心思想:
不是找分隔超平面,而是找一个 “回归带”,让尽可能多的数据点落在带内,带的宽度由参数 ε 控制。
代码:SVR 回归对比(线性 vs RBF 核)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成非线性回归数据
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = np.sin(X).ravel() + 0.1 * np.random.randn(100) # 正弦曲线+噪声
# 2. 训练SVR(线性核 vs RBF核)
svr_linear = SVR(kernel='linear', C=100, epsilon=0.1)
svr_rbf = SVR(kernel='rbf', C=100, epsilon=0.1, gamma='scale')
svr_linear.fit(X, y)
svr_rbf.fit(X, y)
# 3. 预测
y_pred_linear = svr_linear.predict(X)
y_pred_rbf = svr_rbf.predict(X)
# 4. 评估
mse_linear = mean_squared_error(y, y_pred_linear)
mse_rbf = mean_squared_error(y, y_pred_rbf)
print("=== 核回归(SVR)评估 ===")
print(f"线性核MSE:{mse_linear:.4f}")
print(f"RBF核MSE:{mse_rbf:.4f}")
# 5. 可视化对比
plt.figure(figsize=(12, 6))
# 子图1:线性核SVR
plt.subplot(1, 2, 1)
plt.scatter(X, y, s=50, alpha=0.8, label='真实数据', color='blue')
plt.plot(X, y_pred_linear, 'r-', linewidth=2, label='线性核SVR')
plt.fill_between(X.ravel(), y_pred_linear - 0.1, y_pred_linear + 0.1, alpha=0.2, color='red')
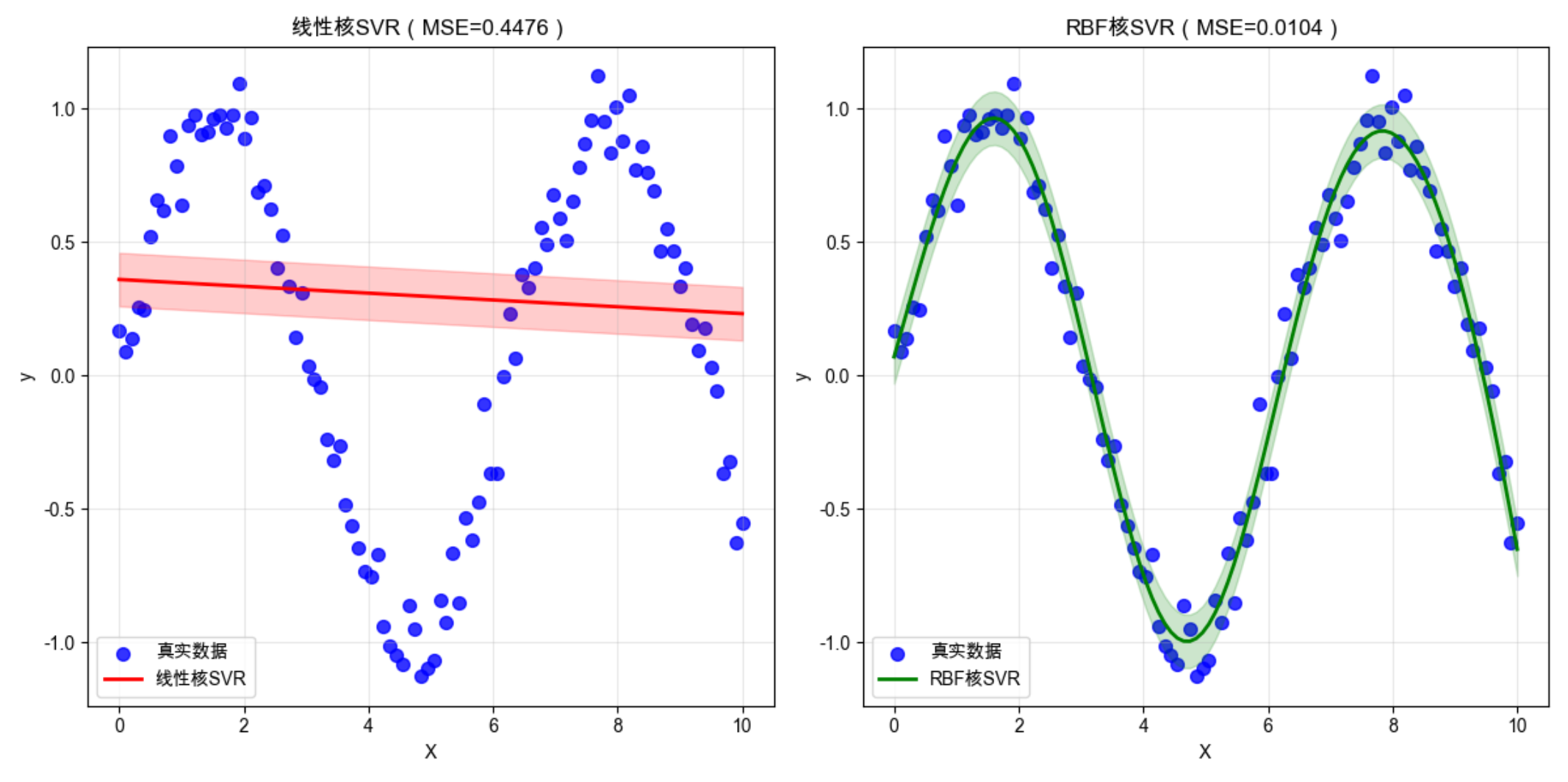
plt.title(f'线性核SVR(MSE={mse_linear:.4f})', fontsize=12)
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(alpha=0.3)
# 子图2:RBF核SVR
plt.subplot(1, 2, 2)
plt.scatter(X, y, s=50, alpha=0.8, label='真实数据', color='blue')
plt.plot(X, y_pred_rbf, 'g-', linewidth=2, label='RBF核SVR')
plt.fill_between(X.ravel(), y_pred_rbf - 0.1, y_pred_rbf + 0.1, alpha=0.2, color='green')
plt.title(f'RBF核SVR(MSE={mse_rbf:.4f})', fontsize=12)
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
代码解释
- 生成正弦曲线 + 噪声的非线性回归数据
epsilon:回归带的宽度,控制允许的误差范围- 对比线性核和 RBF 核的 MSE:RBF 核更适合非线性回归
运行效果
- 线性核 SVR 只能拟合直线,无法捕捉正弦曲线的非线性趋势
- RBF 核 SVR 能完美拟合非线性数据,MSE 远低于线性核
13.11 用于排名的核机器

核心概念
排名核机器(Kernel Ranking)用于排序任务(比如推荐系统、搜索结果排序),核心是:
学习一个排序函数,让相关的样本排在前面,不相关的排在后面。
代码:核排序实战(简单版)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.metrics import ndcg_score # NDCG:排名评估指标
from sklearn.metrics.pairwise import rbf_kernel # 导入RBF核函数
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成排名数据(特征:[相关性特征1, 相关性特征2],标签:相关性分数0-5)
np.random.seed(42)
X = np.random.rand(100, 2) * 10 # 100个样本,2个相关性特征
y = (X[:, 0] + X[:, 1]).astype(int) % 6 # 相关性分数0-5
# 2. 转换为排名任务(分类式排名)
# 把相关性分数作为类别,训练核机器
svm_rank = SVC(kernel='rbf', gamma='scale', probability=True)
svm_rank.fit(X, y)
# 3. 预测排名(按概率排序)
# 选一个查询样本,对所有样本排序
query_idx = 0
query_X = X[query_idx:query_idx+1]
# 关键修正:手动计算gamma值(和sklearn 'scale'模式一致)
# sklearn中gamma='scale'的计算规则:gamma = 1 / (n_features * X.var())
n_features = X.shape[1]
X_var = X.var()
gamma = 1 / (n_features * X_var) if X_var != 0 else 1.0 # 避免除零
# 计算所有样本与查询样本的RBF核相似度
similarity = rbf_kernel(X, query_X, gamma=gamma).ravel()
# 按相似度降序排列
ranked_idx = np.argsort(-similarity) # 降序排列
ranked_y = y[ranked_idx]
# 4. 评估排名效果(NDCG:归一化折损累积增益,越接近1越好)
true_relevance = y.reshape(1, -1)
pred_relevance = similarity.reshape(1, -1)
ndcg = ndcg_score(true_relevance, pred_relevance)
print("=== 核排名评估 ===")
print(f"计算的gamma值:{gamma:.6f}")
print(f"NDCG分数:{ndcg:.4f}")
# 5. 可视化排名结果
plt.figure(figsize=(10, 8))
# 绘制所有样本,颜色表示相关性分数
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap='RdYlGn', alpha=0.8)
# 标记查询样本
plt.scatter(X[query_idx, 0], X[query_idx, 1], s=200, marker='*', color='black', label='查询样本')
# 绘制排名顺序(前10个)
for i, idx in enumerate(ranked_idx[:10]):
plt.annotate(f'{i+1}', (X[idx, 0], X[idx, 1]), fontsize=12, ha='center', va='center', color='white')
plt.colorbar(scatter, label='相关性分数(越高越相关)')
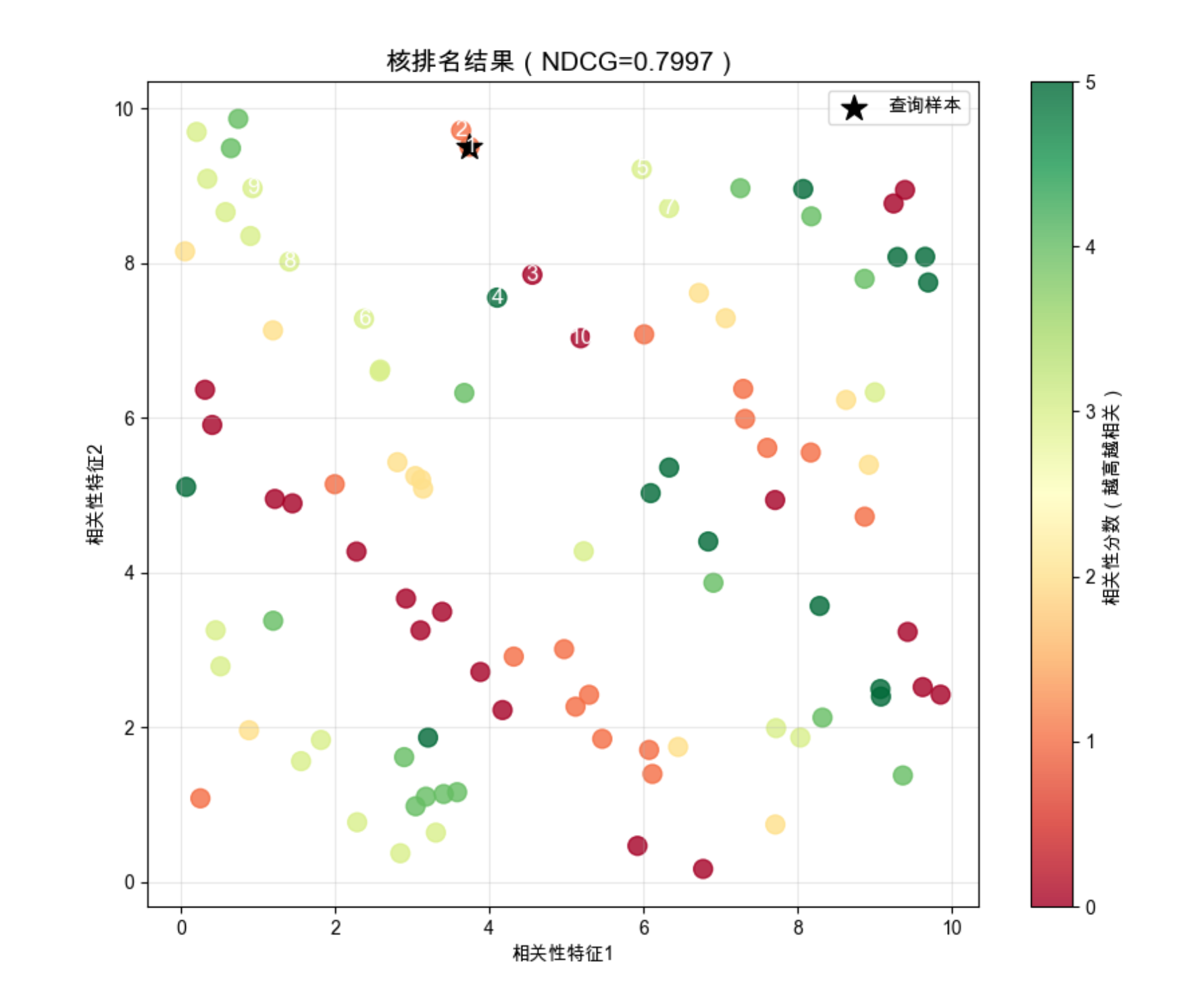
plt.title(f'核排名结果(NDCG={ndcg:.4f})', fontsize=14)
plt.xlabel('相关性特征1')
plt.ylabel('相关性特征2')
plt.legend()
plt.grid(alpha=0.3)
plt.show()代码解释
ndcg_score:排名任务的核心评估指标,值越接近 1,排名效果越好- 核排名的核心:通过核函数计算样本间的相似度,按相似度排序
- 可视化:数字标注前 10 个样本的排名,颜色越深表示相关性越高
运行效果
- 核排名能根据样本间的相似度,把高相关性的样本排在前面
- NDCG 分数接近 1,说明排名效果好
13.12 一类核机器
核心概念
一类核机器(One-Class SVM)用于异常检测 / 新奇性检测,核心思想:
只学习正常样本的分布,把偏离分布的样本标记为异常。
代码:一类 SVM 异常检测
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import OneClassSVM
from sklearn.datasets import make_blobs
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成数据(正常样本 + 异常样本)
X_normal, _ = make_blobs(n_samples=200, centers=1, random_state=42, cluster_std=0.5)
X_outlier = np.random.uniform(low=-5, high=5, size=(20, 2)) # 异常样本
X = np.vstack([X_normal, X_outlier])
y_true = np.hstack([np.ones(200), -np.ones(20)]) # 1=正常,-1=异常
# 2. 训练一类SVM
one_class_svm = OneClassSVM(kernel='rbf', gamma='scale', nu=0.1) # nu=异常样本比例
one_class_svm.fit(X_normal)
# 3. 预测
y_pred = one_class_svm.predict(X)
# 计算准确率
accuracy = np.mean(y_pred == y_true)
print("=== 一类核机器(异常检测) ===")
print(f"异常检测准确率:{accuracy:.2f}")
# 4. 可视化异常检测结果
plt.figure(figsize=(10, 8))
# 绘制正常样本和异常样本
plt.scatter(X_normal[:, 0], X_normal[:, 1], c='blue', s=50, alpha=0.8, label='正常样本')
plt.scatter(X_outlier[:, 0], X_outlier[:, 1], c='red', s=100, marker='x', label='真实异常')
# 绘制决策边界
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()
xx = np.linspace(xlim[0], xlim[1], 100)
yy = np.linspace(ylim[0], ylim[1], 100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = one_class_svm.decision_function(xy).reshape(XX.shape)
# 绘制决策边界(0是正常/异常的分界)
plt.contour(XX, YY, Z, levels=[0], colors='k', alpha=0.8, linewidths=2)
plt.contourf(XX, YY, Z, levels=np.linspace(Z.min(), 0, 10), alpha=0.2, colors='red')
plt.contourf(XX, YY, Z, levels=np.linspace(0, Z.max(), 10), alpha=0.2, colors='blue')
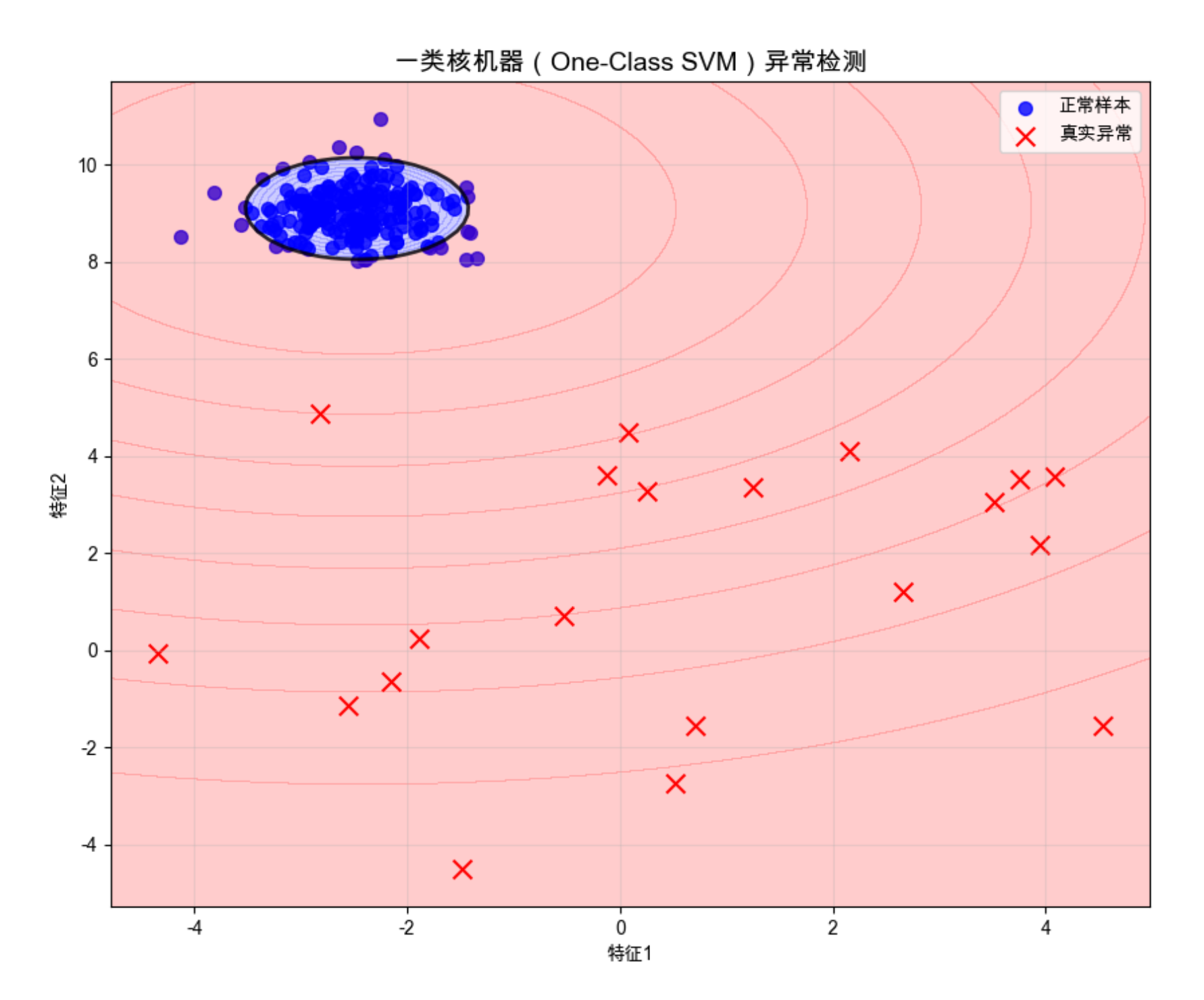
plt.title('一类核机器(One-Class SVM)异常检测', fontsize=14)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)
plt.show()
代码解释
nu参数:指定异常样本的比例(这里设为 0.1,表示 10% 的异常样本)decision_function:输出样本到决策边界的距离,小于 0 是异常,大于 0 是正常- 可视化:红色区域是异常,蓝色区域是正常
运行效果
- 一类 SVM 能准确识别出偏离正常分布的异常样本
- 决策边界能很好地包围正常样本,把异常样本排除在外
13.13 大边缘最近邻分类

核心概念
大边缘最近邻(Large Margin Nearest Neighbor,LMNN)是核机器 + KNN 的结合,核心思想:
学习一个距离度量,让同类样本的距离更近,异类样本的距离更远(大边缘)。
代码:LMNN 分类实战
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_moons
from sklearn.metrics import accuracy_score
from metric_learn import LMNN # 需要安装:pip install metric-learn
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成数据
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
X_train, X_test = X[:150], X[150:]
y_train, y_test = y[:150], y[150:]
# 2. 传统KNN vs LMNN-KNN
# 传统KNN
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_pred_knn = knn.predict(X_test)
acc_knn = accuracy_score(y_test, y_pred_knn)
# LMNN(学习距离度量)
lmnn = LMNN(k=5, learn_rate=1e-3)
lmnn.fit(X_train, y_train)
# 转换数据到新的距离空间
X_train_lmnn = lmnn.transform(X_train)
X_test_lmnn = lmnn.transform(X_test)
# LMNN-KNN
knn_lmnn = KNeighborsClassifier(n_neighbors=5)
knn_lmnn.fit(X_train_lmnn, y_train)
y_pred_lmnn = knn_lmnn.predict(X_test_lmnn)
acc_lmnn = accuracy_score(y_test, y_pred_lmnn)
# 3. 打印结果
print("=== 大边缘最近邻分类 ===")
print(f"传统KNN准确率:{acc_knn:.2f}")
print(f"LMNN-KNN准确率:{acc_lmnn:.2f}")
# 4. 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 子图1:原始空间KNN
axes[0].scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
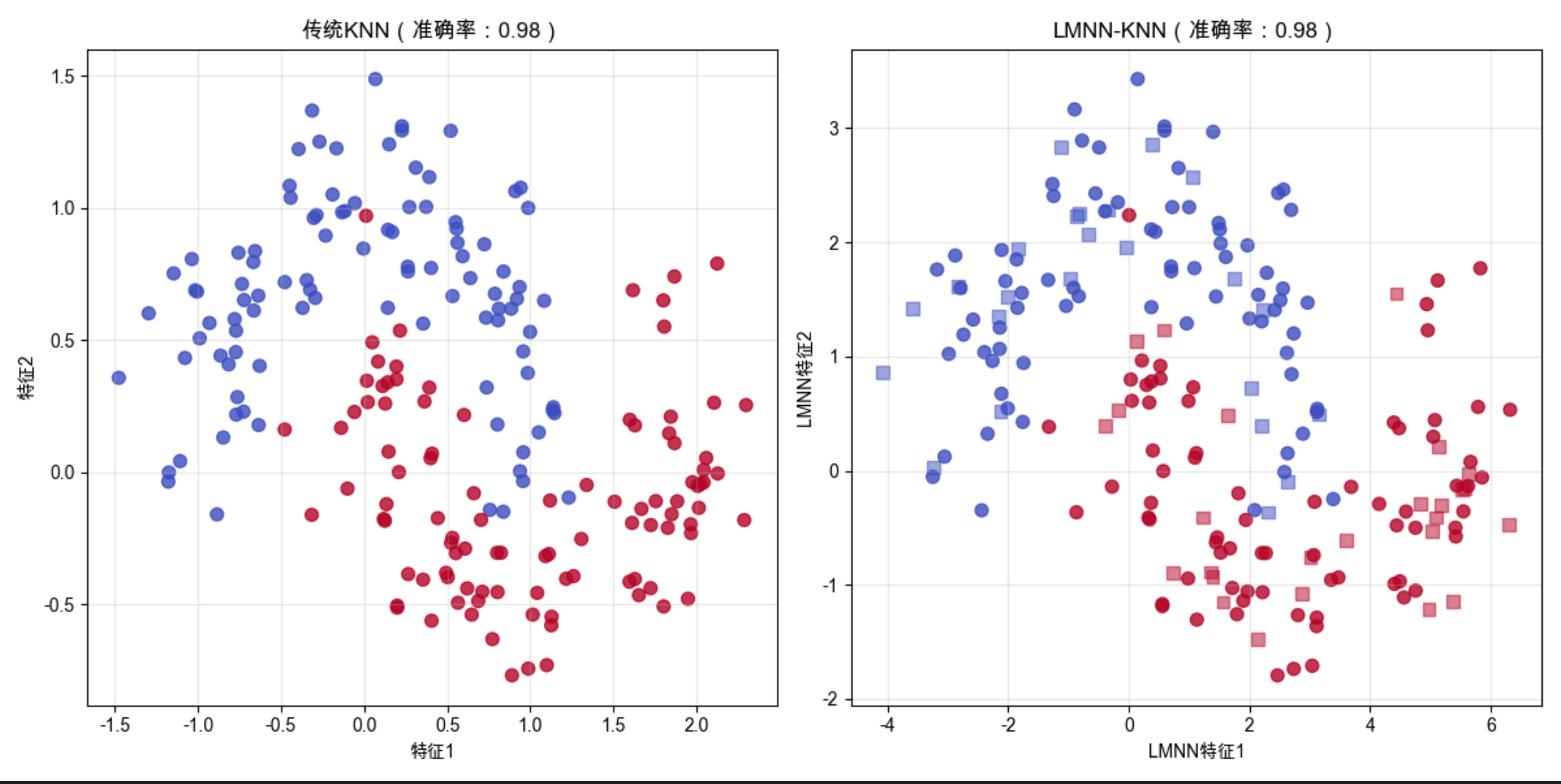
axes[0].set_title(f'传统KNN(准确率:{acc_knn:.2f})', fontsize=12)
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')
axes[0].grid(alpha=0.3)
# 子图2:LMNN空间KNN
axes[1].scatter(X_train_lmnn[:, 0], X_train_lmnn[:, 1], c=y_train, s=50, cmap='coolwarm', alpha=0.8)
axes[1].scatter(X_test_lmnn[:, 0], X_test_lmnn[:, 1], c=y_test, s=50, cmap='coolwarm', alpha=0.5, marker='s')
axes[1].set_title(f'LMNN-KNN(准确率:{acc_lmnn:.2f})', fontsize=12)
axes[1].set_xlabel('LMNN特征1')
axes[1].set_ylabel('LMNN特征2')
axes[1].grid(alpha=0.3)
plt.tight_layout()
plt.show()
代码解释
metric-learn库:提供 LMNN 等距离度量学习算法(需要先安装)- LMNN 的核心:学习一个线性变换,让同类样本更紧凑,异类样本更分散
- 对比传统 KNN 和 LMNN-KNN:LMNN 通常能提升准确率
运行效果
- LMNN 转换后的特征空间,同类样本更集中,异类样本更分散
- LMNN-KNN 的准确率高于传统 KNN,尤其是在噪声数据上
13.14 核维度归约

核心概念
核维度归约(Kernel PCA)是PCA + 核技巧,核心思想:
把高维数据通过核技巧映射到高维空间,再在高维空间做 PCA 降维,得到低维的非线性特征。
代码:Kernel PCA 降维对比(PCA vs Kernel PCA)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 生成环形数据(PCA无法降维分离)
X, y = make_circles(n_samples=400, noise=0.1, factor=0.2, random_state=42)
# 2. PCA vs Kernel PCA
# 传统PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Kernel PCA(RBF核)
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=1.0)
X_kpca = kpca.fit_transform(X)
# 3. 可视化对比
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 子图1:原始数据
axes[0].scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
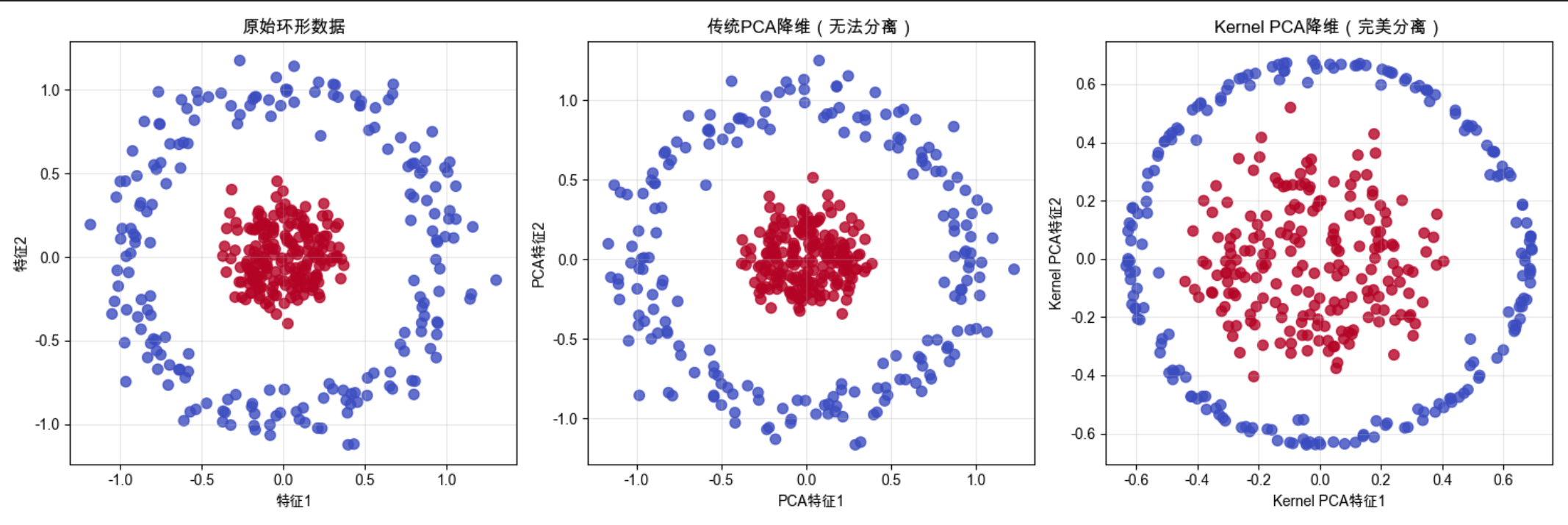
axes[0].set_title('原始环形数据', fontsize=12)
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')
axes[0].grid(alpha=0.3)
# 子图2:PCA降维
axes[1].scatter(X_pca[:, 0], X_pca[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
axes[1].set_title('传统PCA降维(无法分离)', fontsize=12)
axes[1].set_xlabel('PCA特征1')
axes[1].set_ylabel('PCA特征2')
axes[1].grid(alpha=0.3)
# 子图3:Kernel PCA降维
axes[2].scatter(X_kpca[:, 0], X_kpca[:, 1], c=y, s=50, cmap='coolwarm', alpha=0.8)
axes[2].set_title('Kernel PCA降维(完美分离)', fontsize=12)
axes[2].set_xlabel('Kernel PCA特征1')
axes[2].set_ylabel('Kernel PCA特征2')
axes[2].grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 4. 降维后分类效果
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
# PCA降维后分类
svm_pca = SVC(kernel='linear').fit(X_pca, y)
acc_pca = accuracy_score(y, svm_pca.predict(X_pca))
# Kernel PCA降维后分类
svm_kpca = SVC(kernel='linear').fit(X_kpca, y)
acc_kpca = accuracy_score(y, svm_kpca.predict(X_kpca))
print("=== 核维度归约评估 ===")
print(f"PCA降维后线性SVM准确率:{acc_pca:.2f}")
print(f"Kernel PCA降维后线性SVM准确率:{acc_kpca:.2f}")
代码解释
- 传统 PCA:线性降维,无法分离环形数据
- Kernel PCA:非线性降维,通过 RBF 核把环形数据映射到高维,再降维,实现线性可分
- 降维后分类:Kernel PCA 降维后的特征,用简单的线性 SVM 就能达到 100% 准确率
运行效果
- 核维度归约能处理传统 PCA 无法处理的非线性数据
- 是高维非线性数据降维的重要工具
13.15 注释

- 核机器的核心是核技巧,避免了高维计算的维度灾难
- SVM 的参数调优重点:
C(惩罚系数)、gamma(RBF 核带宽)、nu(ν-SVM 容错率) - 核函数选择:优先用 RBF 核(万能核),线性数据用线性核,多项式数据用多项式核
- 核机器的优缺点:优点:泛化能力强、适合小样本、能处理高维数据;缺点:训练速度慢(不适合超大数据集)、解释性差
13.16 习题
- 尝试修改 RBF 核的
gamma参数,观察决策边界的变化(gamma 越大,模型越复杂) - 用真实数据集(如鸢尾花、MNIST)测试多核学习的效果
- 对比 One-Class SVM 和孤立森林的异常检测效果
- 用 Kernel PCA 对自己的数据集进行降维,并评估分类效果
13.17 参考文献
- 《机器学习导论》(Ethem Alpaydin 著)
- 《统计学习方法》(李航 著)
- Scikit-learn 官方文档:https://scikit-learn.org/stable/modules/svm.html
- Metric-learn 官方文档:https://metric-learn.readthedocs.io/
总结

1.核机器核心:通过核技巧将低维非线性数据映射到高维线性可分空间,核心代表是 SVM,关键参数有C(惩罚)、gamma(核带宽)、nu(容错率)。
2.核机器应用:不仅能做二分类,还能扩展到多分类、回归、排名、异常检测、降维等场景,是机器学习的 “万能工具”。
3.可视化关键:线性核适合线性数据,RBF 核是通用选择,多核学习能取长补短,Kernel PCA 解决非线性降维问题。
希望这篇文章能帮你彻底搞懂核机器!所有代码都能直接运行,建议动手跑一遍,修改参数看看效果,加深理解。如果有问题,欢迎在评论区交流~
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容








所有评论(0)