1.边缘

边缘是像素的突变位置。

2.常见边缘检测算法

通过找到一阶导数的极值点或者二阶导数的过零点来确定边缘像素的位置。边缘检测通常使用算子，即特定的卷积核。通过差分对离散的像素点求导，然后转化成卷积核进行卷积。使用卷积统一涵盖求导，高斯平滑等操作。

---

2.1 正交梯度算子：一阶差分算子

• 由于差分运算会放大噪声影响，一般事先对图像做高斯平滑预处理
• 等价于高斯函数梯度与图像做卷积

$$J_{\sigma }(x)=\nabla \left[G_{\sigma }(x)\ast I(x)\right]=\left[\nabla G_{\sigma }\right](x)\ast I(x)$$
其中：
$$\nabla G_{\sigma }(x)=\left(\frac{\partial G_{\sigma }}{\partial x},\frac{\partial G_{\sigma }}{\partial y}\right)(x)=\left(-\frac{x}{{\sigma }^2},-\frac{y}{{\sigma }^2}\right)G_{\sigma }(x)$$

$$G_{\sigma }(x)=\frac{1}{2\pi {\sigma }^2}\exp \left(-\frac{x^2+y^2}{2{\sigma }^2}\right)$$

2.1.1Sobel 算子

原理

• 核心思想：通过计算图像中像素点的水平（X方向）和垂直（Y方向）梯度来检测边缘。
• 数学基础：使用两个3×3的卷积核分别对图像进行卷积运算，计算梯度。
  • 水平核（检测垂直边缘）：

    [-1, 0, 1]
    [-2, 0, 2]
    [-1, 0, 1]
    

  • 垂直核（检测水平边缘）：

    [-1, -2, -1]
    [ 0,  0,  0]
    [ 1,  2,  1]
    

• 梯度计算：
  • 水平梯度 $G_x$ 和垂直梯度 $G_y$ 通过卷积得到。
  • 总梯度幅值：$G=\sqrt{G_x^2+G_y^2}$，或近似为 $|G_x|+|G_y|$。

步骤

1. 用水平核和垂直核分别对图像卷积。
2. 计算每个像素的梯度幅值。
3. 设定阈值，幅值高于阈值的像素标记为边缘。

优缺点

• 优点：计算简单，速度快，适合实时处理。
• 缺点：对噪声敏感，边缘较粗，定位精度较低。

应用场景

• 快速检测图像中的明显边缘，如工业零件轮廓检测。

推导
Sobel 算子的卷积核设计并非随意构造，而是基于一阶导数的近似计算与噪声抑制的平衡。其核心思想是将高斯平滑与微分运算结合，从而在检测边缘的同时减少噪声干扰。以下从数学角度逐步推导其设计原理：

---

1. 一阶导数的离散近似
边缘对应图像中亮度函数的突变区域，数学上可通过计算梯度（一阶导数）来检测。在离散图像中，导数需用差分近似：

• 水平方向导数（检测垂直边缘）：
  $$\frac{\partial f}{\partial x}\approx f(x+1,y)-f(x-1,y)$$
  对应的水平差分核为：([-1, 0, 1])。

• 垂直方向导数（检测水平边缘）：
  $$\frac{\partial f}{\partial y}\approx f(x,y+1)-f(x,y-1)$$
  对应的垂直差分核为：$[1,0,-1{]}^T$。

---

2. 高斯平滑的引入
直接差分对噪声敏感。为了抑制噪声，需先对图像进行平滑（低通滤波）。Sobel 算子采用类似高斯平滑的加权平均，权值按距离递减：

• 一维高斯平滑核（简化为 3 点）：
  $$[1,2,1]$$
  中间权值更大，强调当前像素及其邻域。

---

3. 卷积核的合成
Sobel 核的本质是平滑与微分的联合操作，通过将高斯平滑核与差分核进行外积运算得到：

水平方向核（Gx）的推导

• 垂直平滑（抑制垂直方向噪声）：
  $${\text{Smooth}}_y=\left[\begin{array}{c}1\\ 2\\ 1\end{array}\right]$$
• 水平差分（检测垂直边缘）：
  $${\text{Derivative}}_x=[-1,0,1]$$
• 外积运算（联合操作）：
  $$G_x={\text{Smooth}}_y\times {\text{Derivative}}_x=\left[\begin{array}{c}1\\ 2\\ 1\end{array}\right]\cdot [-1,0,1]=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$

垂直方向核（Gy）的推导

• 水平平滑（抑制水平方向噪声）：
  $${\text{Smooth}}_x=[1,2,1]$$
• 垂直差分（检测水平边缘）：
  $${\text{Derivative}}_y=\left[\begin{array}{c}1\\ 0\\ -1\end{array}\right]$$
• 外积运算：
  $$G_y={\text{Derivative}}_y\times {\text{Smooth}}_x=\left[\begin{array}{c}1\\ 0\\ -1\end{array}\right]\cdot [1,2,1]=\left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]$$

---

4. 核的对称性与权值分配

• 中间行/列的权值更大：
  高斯平滑核 $1,2,1]$ 的中间权值为 2，使得当前像素对平滑结果的贡献更大，增强了中心敏感性。
• 平滑与微分的分离性：
  核的行和列分别对应平滑和微分方向，例如 $G_x$ 对垂直方向平滑，水平方向微分，从而更专注于检测垂直边缘。

---

5. 与其他算子的对比

• Prewitt 算子：使用均匀平滑核 $[1,1,1]$，抗噪性弱于 Sobel。
• 高斯一阶导数：Sobel 是高斯平滑与简单差分的折中，计算效率更高。

---

2.1.2 Prewitt 算子

原理

• 与Sobel类似，但卷积核权重不同，更注重边缘方向的均匀性。使用均匀平滑核 $[1,1,1]$
• 水平核：

  [-1, 0, 1]
  [-1, 0, 1]
  [-1, 0, 1]
  

• 垂直核：

  [-1, -1, -1]
  [ 0,  0,  0]
  [ 1,  1,  1]
  

• 梯度计算与Sobel相同。

优缺点

• 优点：对垂直和水平方向边缘响应更均衡。
• 缺点：抗噪能力弱，边缘较模糊。

应用场景

• 需要平衡各方向边缘响应的场景，如简单图像分割。

---

2.1.3 Roberts 算子

原理

• 核心思想：基于对角方向的一阶差分检测边缘，未使用高斯平滑。
• 卷积核：
  • 对角线核1：

    [1, 0]
    [0, -1]
    

  • 对角线核2：

    [0, 1]
    [-1, 0]
    

• 梯度计算：
  • $G=\sqrt{(G_1^2+G_2^2)}$，或近似为 $|G_1|+|G_2|$。

优缺点

• 优点：计算极快，适合资源受限场景。
• 缺点：对噪声敏感，仅检测对角边缘。

应用场景

• 简单实时系统，如嵌入式设备中的快速边缘检测。

---

2.2 方向微分算子

基于特定方向上的微分来检测边缘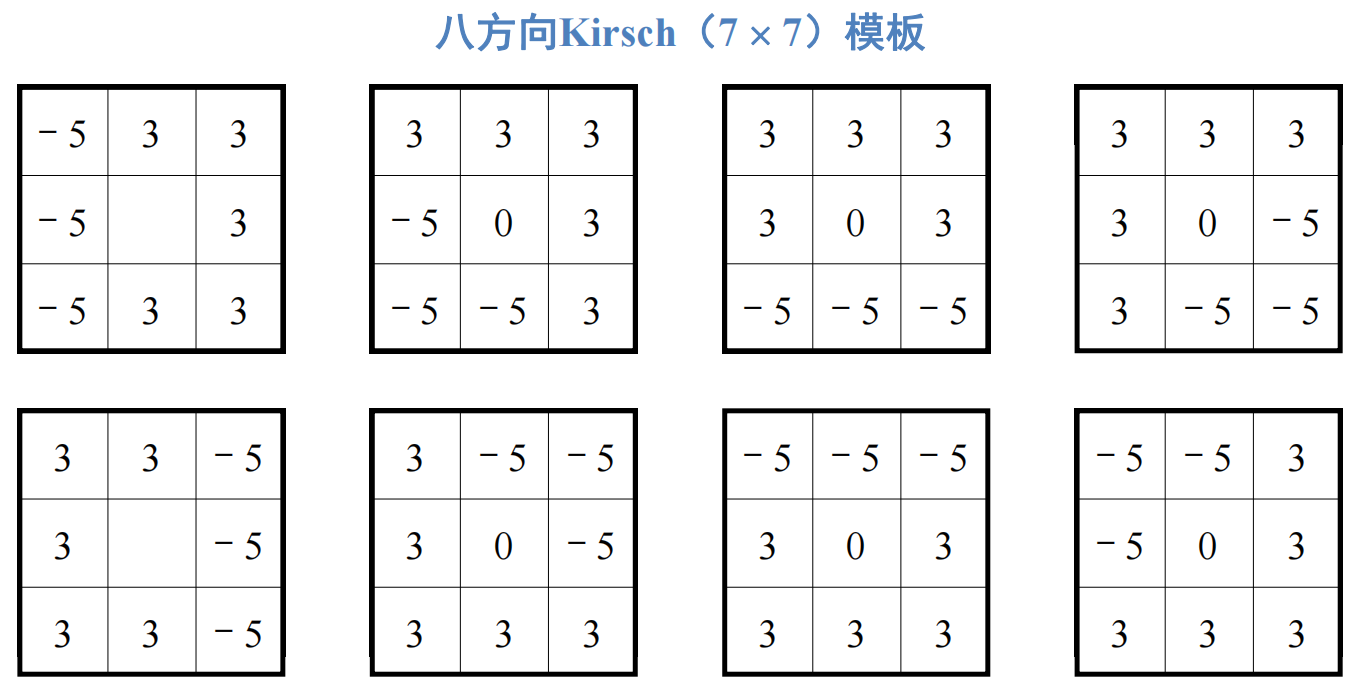

2.3 二阶导数算子

2.3.1 Laplacian 算子

原理
$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

---

二阶导数离散近似

x方向：
$$\frac{{\partial }^{2}f}{\partial x^2}\approx f_x(x+0.5,y)-f_x(x-0.5,y)$$
展开为：
$$=f(x+1,y)-2f(x,y)+f(x-1,y)$$

y方向：
$$\frac{{\partial }^{2}f}{\partial y^2}\approx f_y(x,y+0.5)-f_y(x,y-0.5)$$
展开为：
$$=f(x,y+1)-2f(x,y)+f(x,y-1)$$

• 核心思想：基于二阶导数检测边缘，直接寻找像素值的突变点（梯度变化率为零的点）。
• 卷积核（常用的两种）：
  • 四邻域核：

    [ 0, -1,  0]
    [-1, 4, -1]
    [ 0, -1,  0]
    

  • 八邻域核（增强对角边缘响应）：

    [-1, -1, -1]
    [-1,  8, -1]
    [-1, -1, -1]
    

• 响应特点：
  • 正梯度区域（亮变暗）和负梯度区域（暗变亮）均会产生高响应。产生双像素宽的边缘。无边缘方向信息。
  • 边缘出现在过零点（Zero Crossing）附近。
  • 对噪声想当敏感。

步骤

1. 对图像应用Laplacian核进行卷积。
2. 检测过零点（需配合阈值判断）。

优缺点

• 优点：能同时检测边缘方向和强度，对孤立点敏感。
• 缺点：对噪声极度敏感，通常需先进行高斯滤波（如LOG算法，即Laplacian of Gaussian）。

应用场景

• 结合高斯滤波后用于高精度边缘检测，如医学图像分析。

---

2.3.2 马尔算子

原理
先进行高斯滤波再二阶微分。等价于：高斯函数的二阶导数与图像卷积。

马尔算子的一维函数及频域函数。

2.4 最优边缘检测算子

2.4.1 Canny 算子

原理
Canny算法是一种多步骤优化的边缘检测方法，综合了抗噪能力与边缘定位精度，是实际应用中的黄金标准。
步骤

1. 高斯滤波：

   • 用高斯核平滑图像，抑制噪声。
   • 高斯核示例（σ=1.4）：

     [2, 4, 5, 4, 2]
     [4, 9,12, 9, 4]
     [5,12,15,12, 5]
     [4, 9,12, 9, 4]
     [2, 4, 5, 4, 2]
     

2. 梯度计算：

   • 使用Sobel算子计算水平梯度 $G_x$ 和垂直梯度 $G_y$。
   • 梯度幅值 $G=\sqrt{G_x^2+G_y^2}$，方向 $\theta =\arctan (G_y/G_x)$。

3. 非极大值抑制（NMS）：

   • 在梯度方向上，仅保留幅值最大的像素点，抑制非极大值，使边缘变细。

4. 双阈值处理：

   • 高阈值（$T_{\text{high}}$）：高于此值的像素为强边缘，直接保留。
   • 低阈值（$T_{\text{low}}$）：介于高低阈值之间的像素为弱边缘，仅当与强边缘连通时才保留。
   • 典型阈值比例：$T_{\text{low}}=0.4\times T_{\text{high}}$，例如 $T_{\text{high}}=100$, $T_{\text{low}}=40$。

5. 边缘连接：

   • 通过形态学操作或连通性分析连接断裂的边缘。

优缺点

• 优点：抗噪能力强，边缘连续且细。
• 缺点：计算复杂度高，参数（高低阈值）需手动调整。

应用场景

• 高精度边缘检测，如自动驾驶中的车道线识别、人脸轮廓提取。

---

算法对比总结

算法	抗噪能力	边缘粗细	计算速度	适用场景
Sobel	弱	较粗	快	实时处理、工业检测
Prewitt	弱	较粗	快	平衡各方向边缘
Laplacian	极弱	细	中等	高精度边缘（需滤波后）
Canny	强	细	慢	高精度复杂场景
Roberts	极弱	细	极快	简单实时系统

---

实际应用建议

1. 实时性要求高：选择Sobel或Roberts。
2. 抗噪与精度平衡：优先使用Canny。
3. 简单场景：尝试Laplacian结合高斯滤波（LOG算法）。