我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。
本次2025年高教杯全国大学生数学建模国赛C题可以做如下考虑 (部分公式和代码因为知乎排版问题显示不完整，文中代码仅有部分，完整论文格式标准，包含全部代码)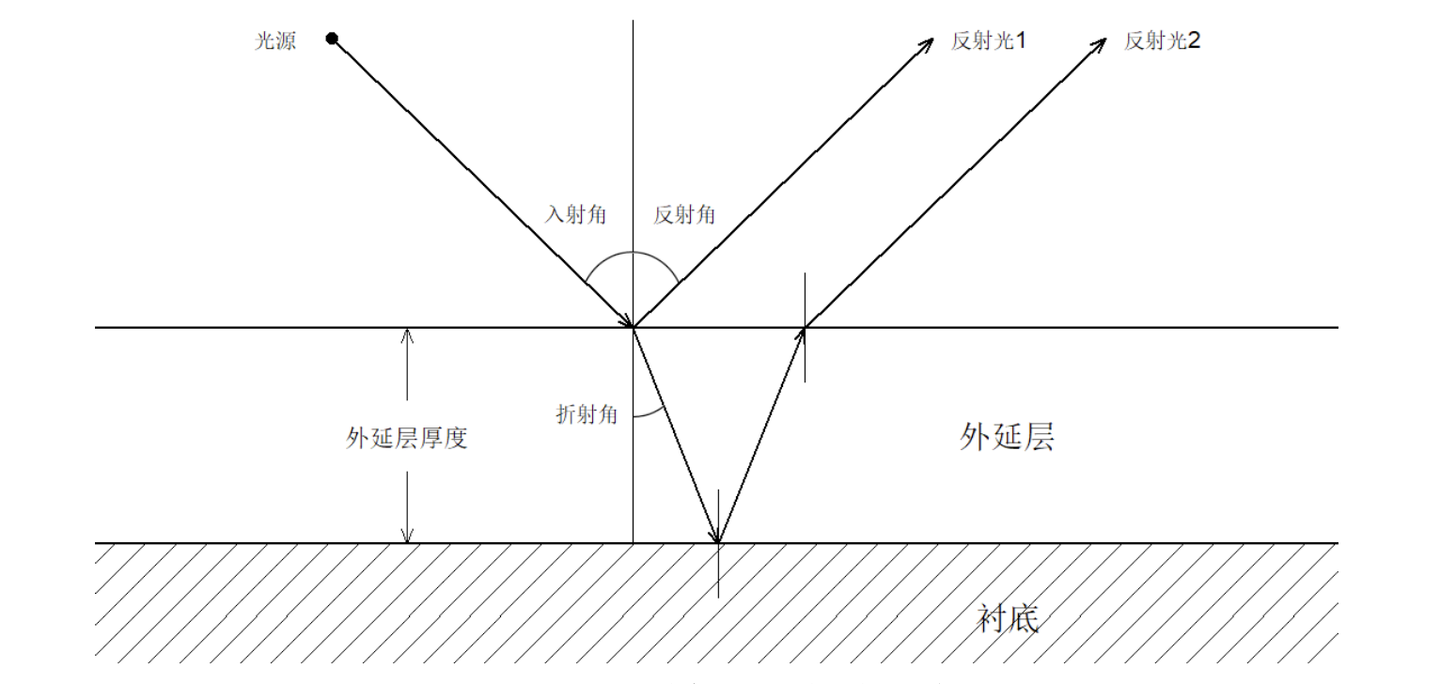

根据题目描述，第一个问题是：

可视化：

问题 1

如果考虑外延层和衬底界面只有一次反射、透射所产生的干涉条纹的情形（图 1），建立确定外延层厚度的数学模型。

这个问题要求：

1. 基于红外干涉法的工作原理
2. 考虑单次反射、透射的简化情况
3. 建立数学模型来确定外延层厚度
4. 模型应该考虑红外光谱的波长、外延层的折射率和红外光的入射角等参数

这是整个题目的基础问题，需要从光学干涉的基本原理出发，推导出外延层厚度与可观测量（如干涉条纹的特征）之间的数学关系。

问题1：外延层厚度测量的数学模型

1. 物理原理分析

根据红外干涉法的工作原理，当红外光入射到外延层时，会在两个界面发生反射：

• 反射光1：从外延层表面（空气-外延层界面）反射
• 反射光2：从衬底表面（外延层-衬底界面）反射

这两束反射光会产生光程差，从而形成干涉条纹。

2. 几何光学分析

设定参数：

• $d$：外延层厚度
• ${\theta }_0$：入射角
• ${\theta }_1$：在外延层中的折射角
• $n_1(\lambda )$：外延层的折射率（与波长相关）
• $n_0=1$：空气的折射率
• $\lambda$：真空中的波长
• $\tilde{\nu }=\frac{1}{\lambda }$：波数

3. 光程差计算

3.1 几何光程差

反射光2相对于反射光1的额外光程为：
$$\Delta L=2d\cos {\theta }_1$$

3.2 折射定律

根据斯涅尔定律：
$$\sin {\theta }_0=n_1(\lambda )\sin {\theta }_1$$

因此：
$$\cos {\theta }_1=\sqrt{1-{\sin }^2{\theta }_1}=\sqrt{1-\frac{{\sin }^2{\theta }_0}{n_1^2(\lambda )}}$$

3.3 光学光程差

考虑在外延层介质中的传播，光学光程差为：
$$\Delta =n_1(\lambda )\cdot \Delta L=2n_1(\lambda )d\cos {\theta }_1$$

代入折射关系：
$$\Delta =2n_1(\lambda )d\sqrt{1-\frac{{\sin }^2{\theta }_0}{n_1^2(\lambda )}}$$

简化为：
$$\Delta =2d\sqrt{n_1^2(\lambda )-{\sin }^2{\theta }_0}$$

4. 干涉条件

4.1 相位差

光学光程差对应的相位差为：
$$\delta =\frac{2\pi }{\lambda }\Delta =2\pi \tilde{\nu }\Delta$$

其中$\tilde{\nu }=\frac{1}{\lambda }$是波数。

4.2 干涉条件

• 相长干涉（极大值）：$\delta =2m\pi$，即$\Delta =m\lambda$
• 相消干涉（极小值）：$\delta =(2m+1)\pi$，即$\Delta =(m+\frac{1}{2})\lambda$

其中$m$为整数。

5. 数学模型

5.1 基本模型

将光学光程差表达式代入干涉条件，得到：

相长干涉条件：
$$2d\sqrt{n_1^2(\tilde{\nu })-{\sin }^2{\theta }_0}=\frac{m}{\tilde{\nu }}$$

相消干涉条件：
$$2d\sqrt{n_1^2(\tilde{\nu })-{\sin }^2{\theta }_0}=\frac{m+0.5}{\tilde{\nu }}$$

5.2 厚度计算公式

解出外延层厚度：
$$d=\frac{m}{2\tilde{\nu }\sqrt{n_1^2(\tilde{\nu })-{\sin }^2{\theta }_0}}$$

或者：
$$d = \frac{m+0.

问题1：外延层厚度确定的数学模型

物理原理分析

根据题目描述，红外光入射到外延层后产生两束反射光：

• 反射光1：从外延层表面直接反射
• 反射光2：透射进入外延层，在外延层-衬底界面反射后再次透射出外延层表面

这两束光存在光程差，在特定条件下会产生干涉条纹。

数学模型推导

1. 几何关系建立

设：

• $d$ = 外延层厚度
• ${\theta }_0$ = 入射角
• ${\theta }_1$ = 外延层内折射角
• $n_1$ = 外延层折射率
• $\lambda$ = 真空中波长
• $\tilde{\nu }$ = 波数 ($\tilde{\nu }=1/\lambda$)

根据斯涅尔定律：
$$\sin {\theta }_0=n_1\sin {\theta }_1$$

2. 光程差计算

反射光2在外延层内的传播路径长度为：
$$L=\frac{2d}{\cos {\theta }_1}$$

考虑折射率，光程为：
$$\delta =n_{1}L=\frac{2n_{1}d}{\cos {\theta }_1}$$

3. 相位差分析

两束反射光的相位差为：
$$\Delta \varphi =\frac{2\pi }{\lambda }\delta =2\pi \tilde{\nu }\cdot \frac{2n_{1}d}{\cos {\theta }_1}$$

利用斯涅尔定律，可得：
$$\cos {\theta }_1=\sqrt{1-{\sin }^2{\theta }_1}=\sqrt{1-\frac{{\sin }^2{\theta }_0}{n_1^2}}$$

因此相位差为：
$$\Delta \varphi =\frac{4\pi \tilde{\nu }{n}_{1}d}{\sqrt{n_1^2-{\sin }^2{\theta }_0}}$$

4. 干涉条件

建设性干涉（亮条纹）条件：
$$\Delta \varphi =2m\pi ,m=0,1,2,\dots$$

即：
$$\frac{4\pi \tilde{\nu }{n}_{1}d}{\sqrt{n_1^2-{\sin }^2{\theta }_0}}=2m\pi$$

简化得：
$$\tilde{\nu }=\frac{m\sqrt{n_1^2-{\sin }^2{\theta }_0}}{2n_{1}d}$$

破坏性干涉（暗条纹）条件：
$$\Delta \varphi =(2m+1)\pi ,m=0,1,2,\dots$$

即：
$$\tilde{\nu }=\frac{(2m+1)\sqrt{n_1^2-{\sin }^2{\theta }_0}}{4n_{1}d}$$

5. 外延层厚度确定模型

对于连续两个相邻亮条纹（或暗条纹），波数差为：
$$\Delta \tilde{\nu }={\tilde{\nu }}_{m+1}-{\tilde{\nu }}_m=\frac{\sqrt{n_1^2-{\sin }^2{\theta }_0}}{2n_{1}d}$$

因此，外延层厚度的数学模型为：

$$\boxed{d=\frac{\sqrt{n_1^2-{\sin }^2{\theta }_0}}{2n_1\Delta \tilde{\nu }}}$$

6. 实用计算公式

当入射角较小时（$\sin
我来帮你解决碳化硅外延层厚度确定的问题。让我从问题1开始，建立数学模型。

问题1：建立确定外延层厚度的数学模型

基于红外干涉法的工作原理，我需要考虑光在外延层和衬底界面的反射和透射。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.optimize import minimize_scalar, curve_fit
from scipy.signal import find_peaks

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

class EpitaxialThicknessModel:
    """外延层厚度测量模型"""
    
    def __init__(self):
        self.c = 2.998e10  # 光速 cm/s
        
    def wavenumber_to_wavelength(self, wavenumber):
        """波数转换为波长 (cm)"""
        return 1.0 / wavenumber
    
    def snells_law(self, n1, theta1, n2):
        """斯涅尔定律计算折射角"""
        sin_theta2 = (n1 / n2) * np.sin(theta1)
        # 确保不超过1
        sin_theta2 = np.clip(sin_theta2, -1, 1)
        return np.arcsin(sin_theta2)
    
    def optical_path_difference(self, thickness, n_epi, theta_incident, n_air=1.0):
        """
        计算光程差
        
        参数:
        thickness: 外延层厚度 (cm)
        n_epi: 外延层折射率
        theta_incident: 入射角 (弧度)
        n_air: 空气折射率
        """
        # 根据斯涅尔定律计算外延层中的折射角
        theta_refracted = self.snells_law(n_air, theta_incident, n_epi)
        
        # 光程差计算
        # 考虑光在外延层中的传播路径
        path_in_epilayer = 2 * thickness / np.cos(theta_refracted)
        optical_path_difference = n_epi * path_in_epilayer - 2 * thickness * np.cos(theta_incident)
        
        return optical_path_difference
    
    def interference_condition(self, thickness, wavelength, n_epi, theta_incident, m=0):
        """
        干涉条件
        
        参数:
        thickness: 外延层厚度
        wavelength: 波长
        n_epi: 外延层折射率
        theta_incident: 入射角
        m: 干涉级数 (整数)
        """
        delta = self.optical_path_difference(thickness, n_epi, theta_incident)
        return delta - m * wavelength
    
    def reflectance_model(self, wavenumber, thickness, n_epi_base, theta_incident_deg):
        """
        反射率模型（考虑干涉效应）
        
        参数:
        wavenumber: 波数 (cm^-1)
        thickness: 外延层厚度 (cm)
        n_epi_base: 基础折射率
        theta_incident_deg: 入射角 (度)
        """
        wavelength = self.wavenumber_to_wavelength(wavenumber)
        theta_incident = np.radians(theta_incident_deg)
        
        # 简化的折射率模型（可以根据实际情况调整）
        n_epi = n_epi_base
        
        # 计算相位差
        delta = self.optical_path_difference(thickness, n_epi, theta_incident)

这个问题需要在保证NIPT准确性（Y染色体浓度≥4%）的前提下，尽可能早地进行检测以降低风险。
更多内容具体可以看看我的下方名片！
里面包含有本次竞赛一手资料与分析！
另外在赛中，我们也会陪大家一起解析建模比赛
记得关注Tina表姐哦～