目录

一、CNN整体结构

1. 从全连接网络到CNN

2. 全连接层的问题

3. CNN的优势

二、卷积层详解

1. 卷积运算基础

2. 填充（Padding）

3. 步幅（Stride）

4. 三维数据的卷积运算

5. 多滤波器机制

6. 批处理

三、池化层

1. 作用与类型

2. Max池化的计算过程

总结

---

一、CNN整体结构

1. 从全连接网络到CNN

        传统的全连接神经网络在处理图像时存在明显局限性，而卷积神经网络通过特殊的层结构更好地处理具有空间结构的数据。

全连接网络结构：

        相邻层的所有神经元之间都有连接

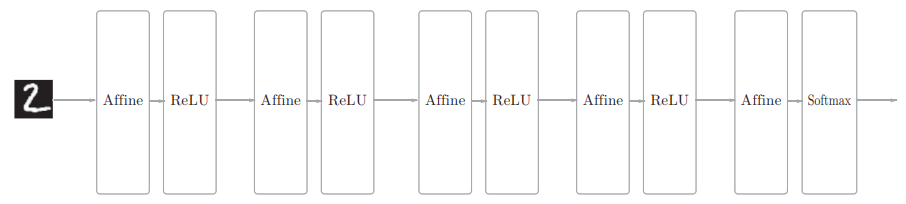
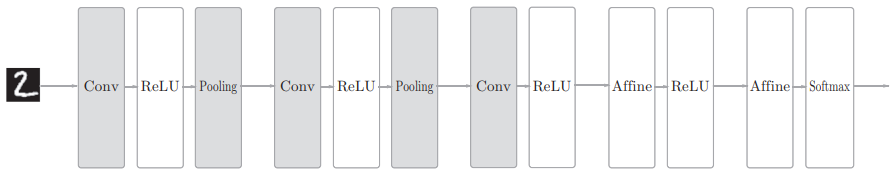
CNN网络结构：

        CNN引入了两种新的层类型替代Affine层：

• 卷积层（Convolution层）

• 池化层（Pooling层）

2. 全连接层的问题

形状信息丢失：

• 全连接层需要将3D图像数据展平为1D向量（把输入（1, 28, 28）的图片数据信息变成784）

• 丢失了像素间的空间关系信息（图片像素点相邻值应该相似）

• 无法利用图像的局部相关性

3. CNN的优势

        在CNN中，各层的输入输出数据称为特征图：

• 输入特征图

• 输出特征图

特征图保持了数据的空间结构，这是CNN能够有效处理图像的关键。

二、卷积层详解

1. 卷积运算基础

        卷积运算相当于图像处理中的滤波器运算，通过滑动窗口在输入数据上应用滤波器。

基本计算过程：

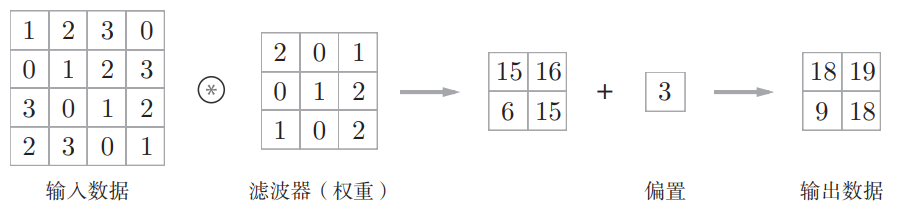
1. 滤波器在输入数据上滑动

2. 对应位置元素相乘后求和

3. 结果保存到输出对应位置

4. 把结果加上偏置求和

2. 填充（Padding）

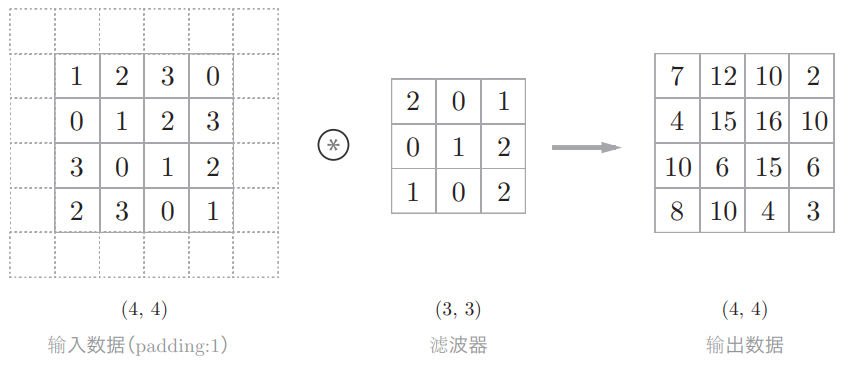
• 在输入数据周围添加固定值（通常是0）

• 目的：控制输出特征图的大小，防止网络过深时特征图尺寸过小

3. 步幅（Stride）

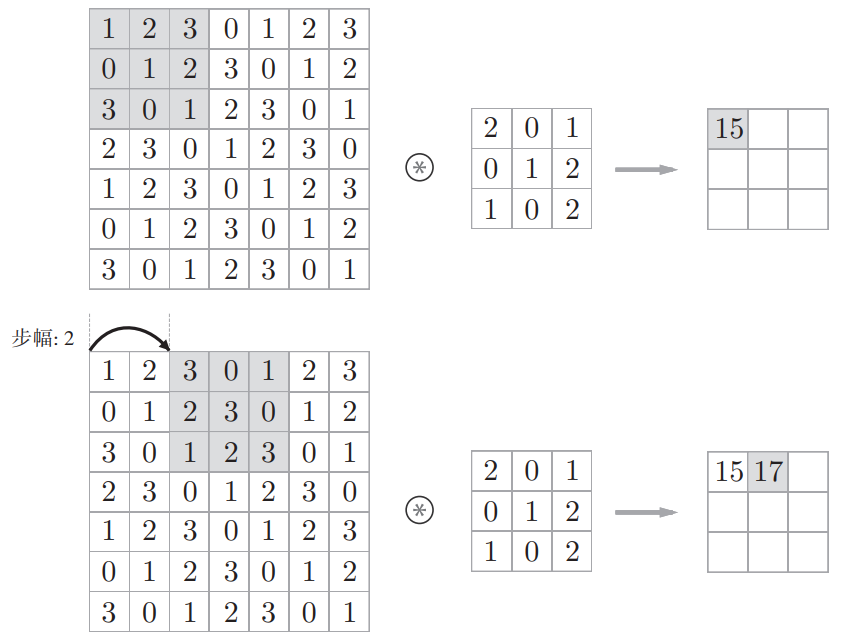
• 滤波器移动的间隔大小

• 步幅增大，输出尺寸减小

• 步幅减小，输出尺寸增大

输出尺寸计算公式：

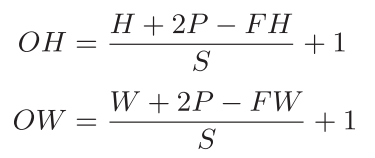
• H, W：输入高和宽

• FH, FW：滤波器高和宽

• P：填充大小

• S：步幅

• OH, OW：输出高和宽

所设定的值必须使输出尺寸计算公式可以除尽，当值无法除尽时，有时会向最接近的整数四舍五入，不进行 报错而继续运行。

4. 三维数据的卷积运算

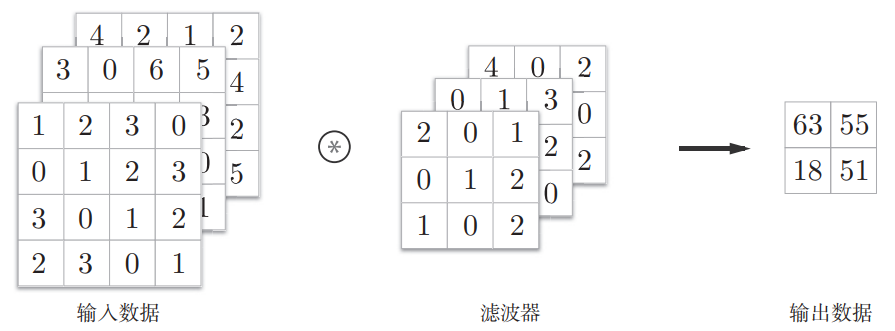
        真实图像是3维数据（通道×高度×宽度），会按通道进行输入数据和滤波器的卷积运算，并将结果相加，从而得到输出。

3D卷积特点：

• 输入数据和滤波器通道数必须相同（输入三层，滤波器也必须是三层）

• 各通道分别进行卷积运算

• 结果相加得到单通道输出，最后只输出一层

数据格式：

• 输入数据：(C, H, W)

• 滤波器：(C, FH, FW)

• 输出数据：(1, OH, OW)

5. 多滤波器机制

        由前文所说，多通道数据在滤波器过后只会输出一层数据，因此为了在通道方向获得多个输出，需要使用多个滤波器，每个滤波器独立提取不同类型的特征。

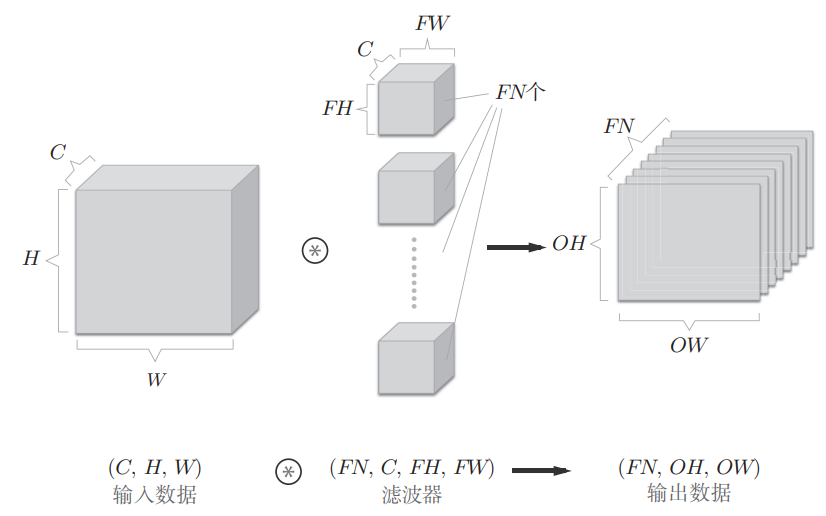
多滤波器配置：

• 滤波器形状变为：(FN, C, FH, FW)

  • FN：滤波器数量

• 输出形状变为：(FN, OH, OW)

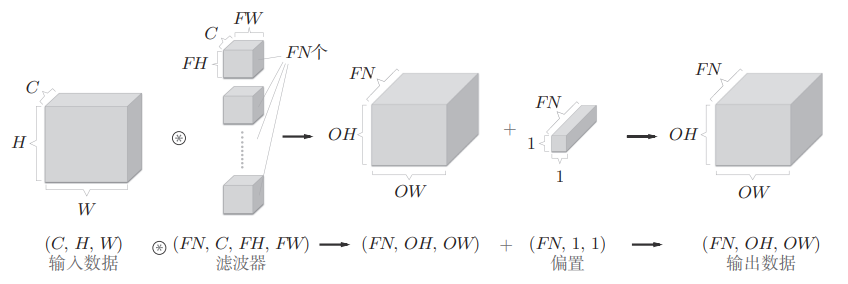
偏置形状：

• 偏置形状：(FN, 1, 1)

• 每个滤波器对应一个偏置值

6. 批处理

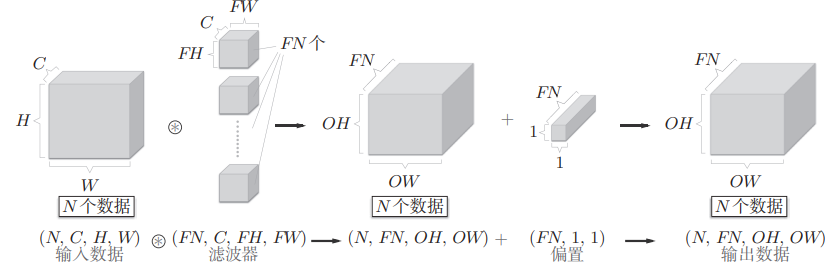
批处理数据格式：

• 输入数据：(N, C, H, W)

• 滤波器：(FN, C, FH, FW)

• 输出数据：(N, FN, OH, OW)

三、池化层

1. 作用与类型

池化层的主要作用是缩小特征图的尺寸，从而减少参数量并增强特征的鲁棒性（稳健性）。

特点：

• 没有要学习的参数
• 通道数不变化
• 对微小的位置变化具有鲁棒性（稳健性）

主要池化类型：

• Max池化：从目标区域中取最大值

• Average池化：计算目标区域的平均值

在图像识别领域，Max池化是最常用的方法。

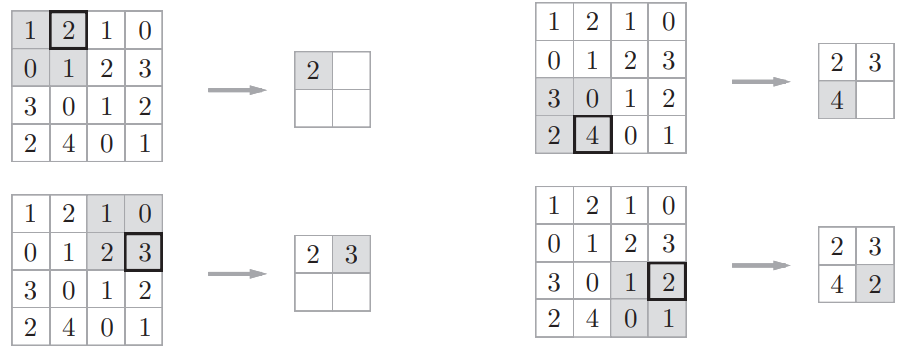
2. Max池化的计算过程

Max池化按指定窗口大小和步幅在输入数据上滑动，取每个区域内的最大值。一般池化的窗口大小会和步幅设定成相同的值。

---

总结

        本文介绍了卷积神经网络(CNN)的基本结构和工作原理。与全连接网络不同，CNN通过卷积层和池化层处理图像数据，保留了空间结构信息。卷积层利用滤波器提取特征，涉及填充、步幅、三维卷积和多滤波器机制；池化层则通过Max池化、Average池化等方法缩小特征图尺寸。这些特性使CNN能有效处理图像数据，在计算机视觉领域展现显著优势。