基于离散拉普拉斯-贝尔特拉米算子(Discrete Laplace-Beltrami Operator, DLBO)的三维人脸面部贴图算法的MATLAB仿真
摘要:本文提出基于离散拉普拉斯-贝尔特拉米算子(DLBO)的三维人脸纹理映射算法。该方法通过构造余切权重DLBO矩阵,建立以曲面微分几何特性为基础的优化目标,实现纹理坐标的参数化映射。算法包含离散算子构造、纹理参数化优化、映射插值及抗锯齿处理等步骤,并通过Matlab仿真验证其在三维人脸模型上的贴图效果。实验结果表明,该方法能有效保持纹理的几何特征,减少失真,适用于计算机视觉和虚拟现实等领域的真实
目录
三维人脸模型贴图是将二维纹理图像精准映射到三维几何模型表面,实现模型视觉真实感增强的关键技术,广泛应用于计算机视觉、虚拟现实(VR)、影视特效等领域。基于离散拉普拉斯 - 贝尔特拉米算子(Discrete Laplace-Beltrami Operator, DLBO)的贴图算法,核心优势在于从曲面内在几何特性出发,通过算子对曲面的光滑性约束和微分几何描述,实现纹理在三维曲面上的保角、保面积或保距离映射,从而避免传统算法的几何失真。其本质是将二维纹理图像的像素信息,通过曲面微分几何的映射关系,“光滑地”铺展到三维人脸模型的三角网格表面。
1.连续形式的拉普拉斯-贝尔特拉米算子定义
拉普拉斯-贝尔特拉米算子是微分几何中定义在黎曼流形(如三维人脸曲面)上的二阶微分算子,是平面拉普拉斯算子在弯曲曲面的自然推广,记为ΔM。其核心作用是描述流形上函数的“曲率”——即函数在某点的局部平均变化率,反映函数在曲面局部的光滑程度。

2.算法实现步骤
三维人脸模型通常以三角网格格式(如OBJ、PLY)存储,包含顶点集V={v1,v2,...,vn}(vi∈R3 )、三角面片集F={f1,f2,...,fm} (每个面片由3个顶点索引构成)。算法步骤如下
2.1 离散拉普拉斯-贝尔特拉米算子构造
DLBO的构造是算法核心,需根据三角网格的几何信息(顶点坐标、面片面积、边长)计算算子矩阵L∈Rn×n 。目前主流的DLBO构造方法有重心坐标法、余切权重法、面积权重法等,其中余切权重法精度较高,且能很好地近似连续LBO的几何特性,成为三维人脸贴图的首选。


余切权重DLBO矩阵L的元素Lij(应顶点vi和vj的关联权重)定义如下:

为了保证算子的数值稳定性和几何一致性,通常对DLBO矩阵进行归一化,得到归一化算子LN.
2.2 纹理参数化的优化目标构建
纹理参数化的核心是求解映射ϕ:vi ↦(ui,vi) ,其中 (ui,vi) 是顶点vi在二维纹理图像中的坐标。为了实现几何失真最小化,需构建以DLBO为约束的优化目标函数。

为了确保纹理图像的关键部位(如眼睛、嘴巴)与三维人脸模型的对应关系准确,需对特征点集S施加硬约束:对于特征点st(对应网格顶点索引为it ),其纹理坐标固定为(uit=ut∗,vit=vt∗),其中 (ut∗ ,v t∗) 是预先指定的目标坐标。
2.3 纹理映射与插值优化
得到所有顶点的纹理坐标后,需将二维纹理图像的像素信息映射到三维网格的三角面片上,核心是解决“面片内部像素的纹理值插值”问题。

由于纹理坐标(u(p),v(p))可能不是纹理图像的整数像素坐标,需通过插值获取对应的像素值。利用周围16个像素的加权平均,插值效果最平滑,适合高精度人脸贴图,公式为:

2.4 抗锯齿处理
为了避免纹理映射后的图像出现锯齿和摩尔纹,需在插值前对纹理图像进行低通滤波(如高斯模糊),或采用多级纹理(Mipmap)技术:预先生成不同分辨率的纹理图像,根据三维模型在渲染时的距离和视角,自动选择合适分辨率的纹理进行映射,平衡精度和性能。
3.matlab仿真测试
clc;
clear;
close all;
warning off;
addpath 'subfunc\myfunc\'
addpath 'subfunc\OBJ_Display\'
load mat_file\eye_change.mat
SEL = 3;%1对正常模型进行脸映射,2对鼻子调整模型进行映射,3对眼皮调整模型进行映射/对鼻子眼皮都调整的模型进行映射
if SEL == 1
vertices_ = vertices;
end
if SEL == 2
vertices_ = new_vertices_nose_change;
end
if SEL == 3
vertices_ = new_vertices_eye_change;
end
figure;
trimesh(faces', vertices_(1,:), vertices_(2,:), vertices_(3,:),'LineWidth',1,'EdgeColor','b');
grid on
axis equal
axis([-110,110,-120,160,-40,120]);
xlabel('x');
ylabel('y');
zlabel('z');
%%
%调用映射算法
A0 = imread('obj_file\head3d.jpg');
[RR,CC,kk] = size(A0);
for i = 1:3
A(:,:,i) = [zeros(650,CC,1);A0(1:RR-170,1:CC,i);zeros(350,CC,1)];
end
[RR,CC,kk] = size(A);
for i = 1:3
A2(:,:,i) = [zeros(RR,300,1),A(1:RR,300:CC-300,i),zeros(RR,307,1)];
end
A3 = imrotate(A2,-2.5,'bicubic','crop');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[RR,CC,kk] = size(A3);
%核心算法,将三维点打散到映射图上
V = vertices_';
F = faces';
uv = func_cem_map(F,V);
xs = CC/2*(uv(:,2)-min(uv(:,2)));
ys = RR/2*(1-uv(:,1)-min(1-uv(:,1)));
figure;%调整,直到对齐为止
plot(xs,ys,'r.')
xlabel('x');
ylabel('y');
figure;%调整,直到对齐为止
imshow(A3);
hold on
plot(xs,RR-ys,'r.')
xlabel('x');
ylabel('y');
Vrgb = zeros(3,length(V));
for i = 1:length(Vrgb)
Vrgb(1,i)=A3(min(floor(RR-ys(i))+1,RR),floor(xs(i))+1,1);
Vrgb(2,i)=A3(min(floor(RR-ys(i))+1,RR),floor(xs(i))+1,2);
Vrgb(3,i)=A3(min(floor(RR-ys(i))+1,RR),floor(xs(i))+1,3);
end
Vrgb=0.9*Vrgb/255;
figure
PlotMesh(F, V, Vrgb');
title('The inputted surface');
pause(0.01)
view([-50,30]);
测试结果如下:
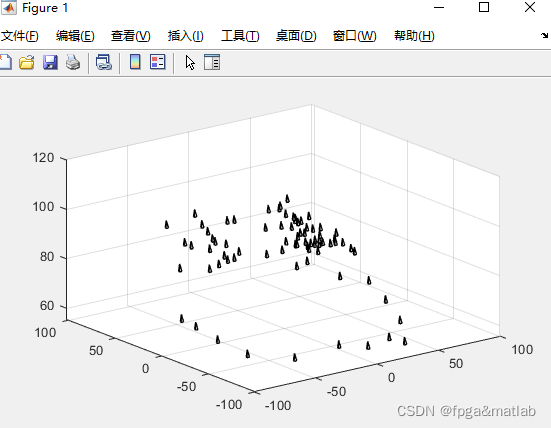
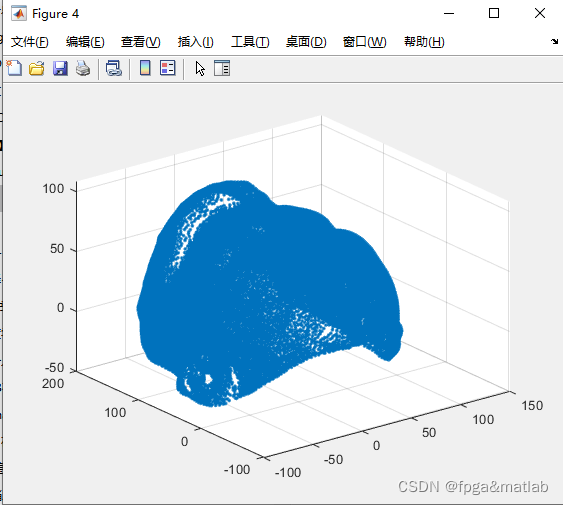
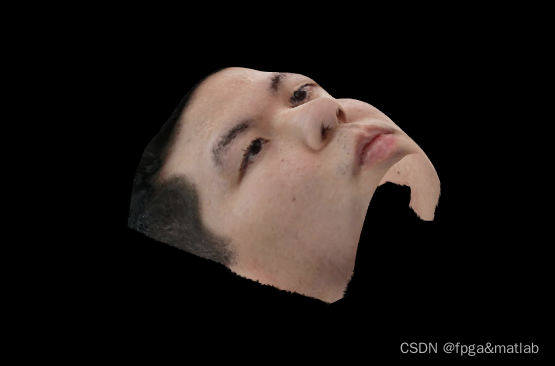
更多推荐
 已为社区贡献21条内容
已为社区贡献21条内容








所有评论(0)