【机器学习案例-26】纽约出租车费预测分析：从数据清洗到机器学习建模全流程

纽约出租车费预测是Kaggle上的一个经典回归预测问题。目标是根据出租车行程的起始时间、起终点经纬度坐标和乘客数量，预测出租车费用。这是一个典型的监督回归机器学习任务。通过本项目的完整实践，我们：✅数据探索：发现并处理了多种异常值✅特征工程：构建了空间、时间等多维度特征✅模型构建：实现了从基线到优化的全流程✅业务洞察：揭示了影响出租车费的关键因素最终成绩验证集RMSE：3.37美元相对于基线提升：

qq_38614074

653人浏览 · 2025-12-23 21:36:14

qq_38614074 · 2025-12-23 21:36:14 发布

🧑 博主简介：曾任某智慧城市类企业算法总监，目前在美国市场的物流公司从事高级算法工程师一职，深耕人工智能领域，精通python数据挖掘、可视化、机器学习等，发表过AI相关的专利并多次在AI类比赛中获奖。CSDN人工智能领域的优质创作者，提供AI相关的技术咨询、项目开发和个性化解决方案等服务，如有需要请站内私信或者联系任意文章底部的的VX名片（ID：xf982831907）

💬 博主粉丝群介绍：① 群内初中生、高中生、本科生、研究生、博士生遍布，可互相学习，交流困惑。② 热榜top10的常客也在群里，也有数不清的万粉大佬，可以交流写作技巧，上榜经验，涨粉秘籍。③ 群内也有职场精英，大厂大佬，可交流技术、面试、找工作的经验。④ 进群免费赠送写作秘籍一份，助你由写作小白晋升为创作大佬。⑤ 进群赠送CSDN评论防封脚本，送真活跃粉丝，助你提升文章热度。有兴趣的加文末联系方式，备注自己的CSDN昵称，拉你进群，互相学习共同进步。

在这里插入图片描述

【机器学习案例-26】纽约出租车费预测分析：从数据清洗到机器学习建模全流程

🚖 本文基于Kaggle纽约出租车费预测竞赛，使用Python进行完整的数据分析、特征工程和机器学习建模，带你一步步构建预测模型。

🎯 一、项目概述

1.1 项目背景

纽约出租车费预测是Kaggle上的一个经典回归预测问题。目标是根据出租车行程的起始时间、起终点经纬度坐标和乘客数量，预测出租车费用。这是一个典型的监督回归机器学习任务。

1.2 数据集特点

数据规模：原始数据5500万行（本文使用500万行）
特征维度：时间、空间、乘客数量等多维度信息
预测目标：fare_amount（出租车费用，单位：美元）

1.3 技术栈

数据处理：Pandas, NumPy
可视化：Matplotlib, Seaborn
机器学习：Scikit-learn
特征工程：自定义函数提取时空特征

📊 二、数据探索与预处理

2.1 数据加载与初探

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor

# 读取500万行数据
data = pd.read_csv('../input/train.csv', nrows = 5_000_000, 
                   parse_dates = ['pickup_datetime']).drop(columns = 'key')
data = data.dropna()  # 删除缺失值

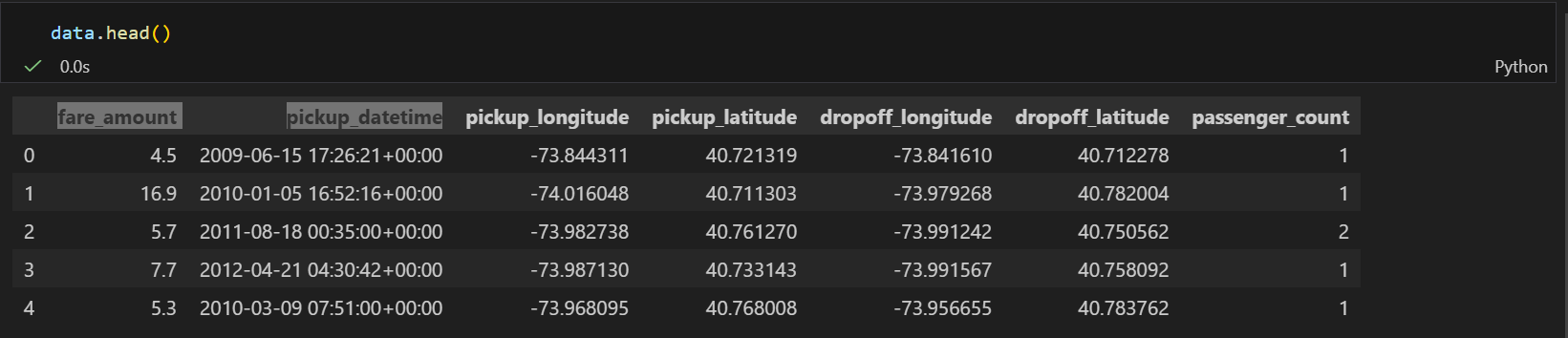
数据概览：

字段	含义	数据类型
fare_amount	出租车费用（目标变量）	float
pickup_datetime	上车时间	datetime
pickup_longitude	上车经度	float
pickup_latitude	上车纬度	float
dropoff_longitude	下车经度	float
dropoff_latitude	下车纬度	float
passenger_count	乘客数量	int

2.2 异常值检测与处理

2.2.1 费用异常值

print(f"负费用数量: {len(data[data['fare_amount'] < 0])}")
print(f"零费用数量: {len(data[data['fare_amount'] == 0])}")
print(f"超过100美元费用数量: {len(data[data['fare_amount'] > 100])}")

# 基于纽约出租车实际收费规则过滤
data = data[data['fare_amount'].between(left = 2.5, right = 100)]

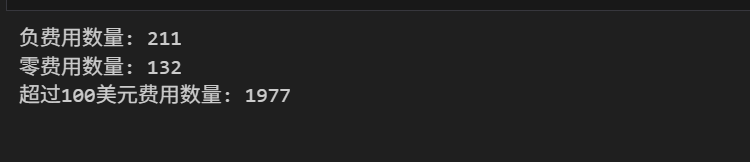
处理结果：

移除负费用：211条
移除0费用：132条
移除>100美元费用：1977条

2.2.2 地理位置异常值

# 移除异常经纬度
print(f"经纬度处理前的数据维度：{data.shape}")
data = data.loc[data['pickup_latitude'].between(40, 42)]
data = data.loc[data['pickup_longitude'].between(-75, -72)]
data = data.loc[data['dropoff_latitude'].between(40, 42)]
data = data.loc[data['dropoff_longitude'].between(-75, -72)]
print(f"经纬度处理后的数据维度：{data.shape}")

2.2.3 乘客数量异常值

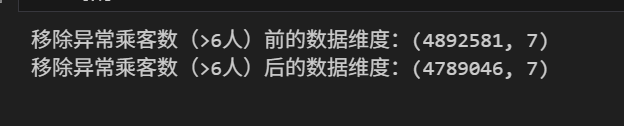
# 移除异常乘客数（>6人）
print(f"移除异常乘客数（>6人）前的数据维度：{data.shape}")
data = data.loc[data['passenger_count'] < 6]
print(f"移除异常乘客数（>6人）后的数据维度：{data.shape}")

2.3 数据可视化分析

费用分布分析

plt.figure(figsize=(10, 6))
sns.distplot(data['fare_amount'])
plt.title('出租车费用分布')
plt.xlabel('费用（美元）')
plt.ylabel('密度')

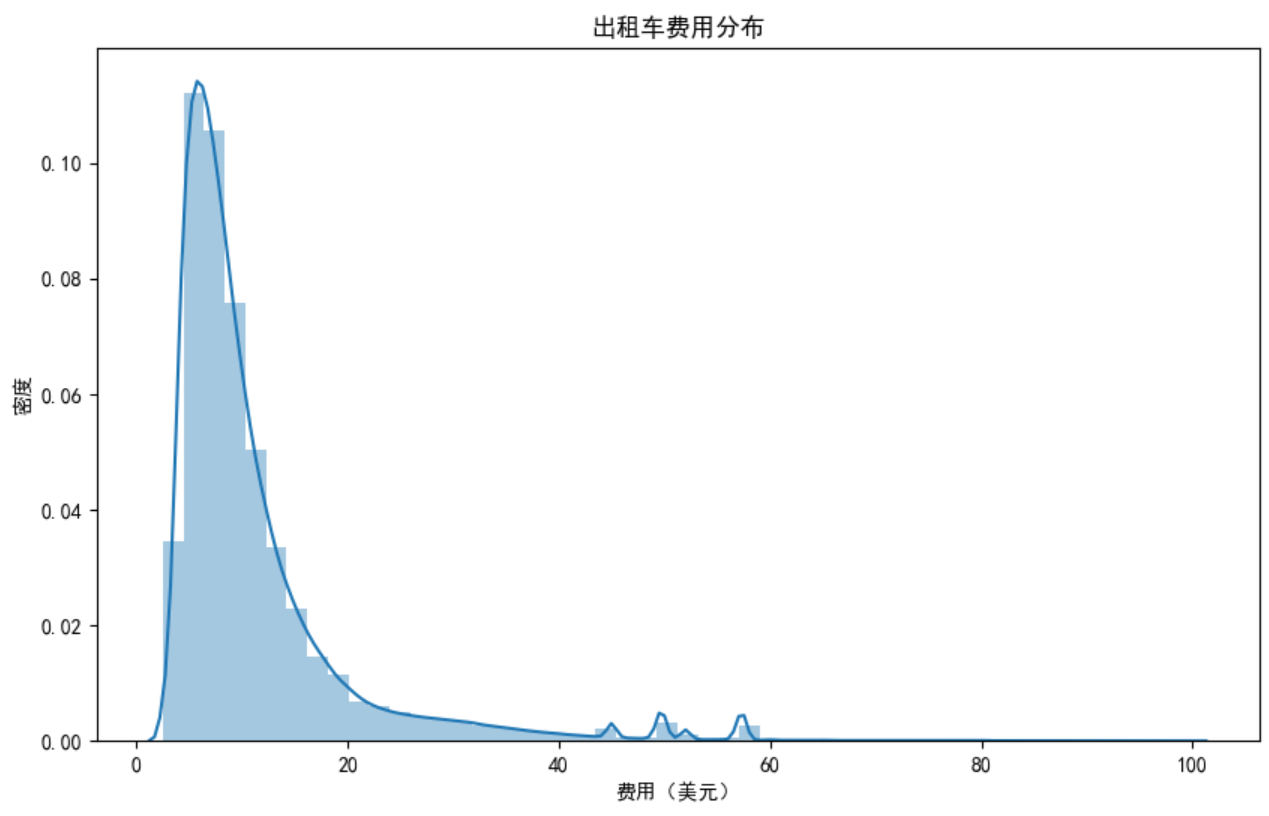
发现：费用呈现右偏分布，大多数行程费用在20美元以内。

地理位置分布

# 绘制纽约地图上的上车位置
nyc_map = plt.imread('nyc_map.png')
BB = (-74.1, -73.7, 40.6, 40.85)

fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.scatter(data.sample(10000)['pickup_longitude'], 
           data.sample(10000)['pickup_latitude'], 
           zorder=1, alpha=0.2, c='r', s=1)
ax.set_xlim((BB[0], BB[1]))
ax.set_ylim((BB[2], BB[3]))
ax.imshow(nyc_map, zorder=0, extent=BB)
plt.title('纽约出租车上车位置分布')

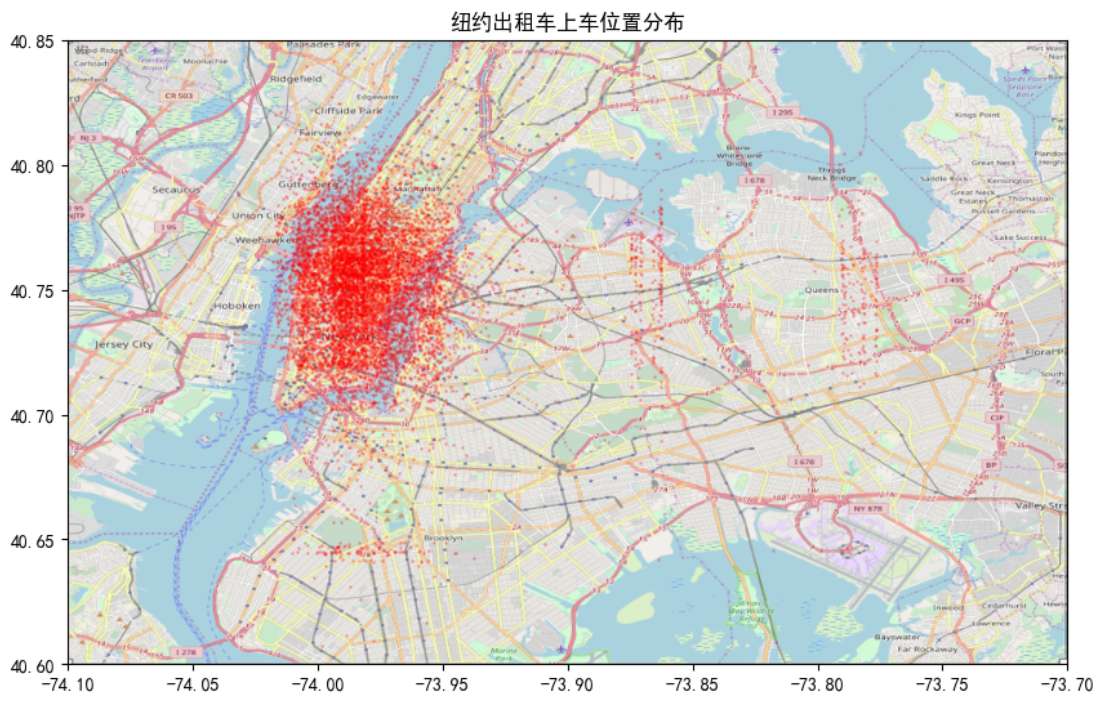
🔧 三、特征工程

3.1 基础空间特征–曼哈顿相对距离

# 绝对经纬度差异
data['abs_lat_diff'] = (data['dropoff_latitude'] - data['pickup_latitude']).abs()
data['abs_lon_diff'] = (data['dropoff_longitude'] - data['pickup_longitude']).abs()

# 曼哈顿距离（相对）
def minkowski_distance(x1, x2, y1, y2, p):
    return ((abs(x2 - x1) ** p) + (abs(y2 - y1)) ** p) ** (1 / p)

data['manhattan'] = minkowski_distance(data['pickup_longitude'], 
                                       data['dropoff_longitude'],
                                       data['pickup_latitude'], 
                                       data['dropoff_latitude'], 1)

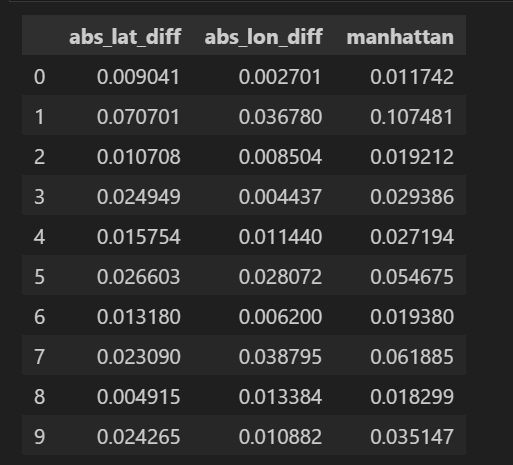
3.2 实际距离计算（Haversine公式）

def haversine_np(lon1, lat1, lon2, lat2):
    """
    计算地球上两点间的大圆距离（Haversine距离）
    单位：千米
    """
    R = 6378  # 地球半径（千米）
    
    lon1, lat1, lon2, lat2 = map(np.radians, [lon1, lat1, lon2, lat2])
    dlon = lon2 - lon1
    dlat = lat2 - lat1
    
    a = np.sin(dlat/2.0)**2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon/2.0)**2
    c = 2 * np.arcsin(np.sqrt(a))
    km = R * c
    
    return km

data['haversine'] = haversine_np(data['pickup_longitude'], data['pickup_latitude'],
                                 data['dropoff_longitude'], data['dropoff_latitude'])

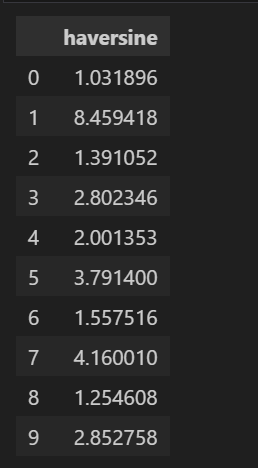
3.3 时间特征提取

def extract_dateinfo(df, date_col, time=True):
    """从日期时间字段提取丰富的时间特征"""
    df = df.copy()
    fld = df[date_col]
    
    # 基础时间特征
    attr = ['Year', 'Month', 'Day', 'Dayofweek', 'Dayofyear', 'Hour', 'Minute', 'Second']
    for n in attr: 
        df['pickup_' + n] = getattr(fld.dt, n.lower())
    
    # 分数时间特征（0-1范围）
    if time:
        df['pickup_frac_day'] = ((df['pickup_Hour']) + 
                                 (df['pickup_Minute'] / 60) + 
                                 (df['pickup_Second'] / 3600)) / 24
        df['pickup_frac_week'] = (df['pickup_Dayofweek'] + df['pickup_frac_day']) / 7
        df['pickup_frac_year'] = (df['pickup_Dayofyear'] + df['pickup_frac_day']) / 365
        
    return df

data = extract_dateinfo(data, 'pickup_datetime')

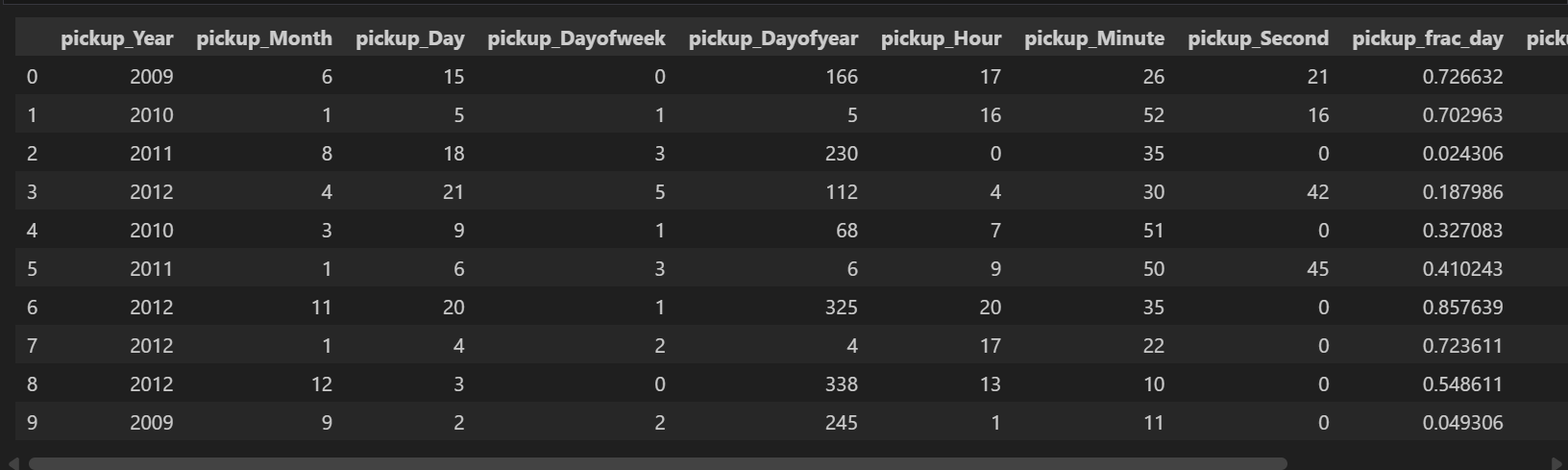
生成的时间特征：

年、月、日、星期、小时等基本特征
一天中的分数时间（0-1）
一周中的分数时间（0-1）
一年中的分数时间（0-1）

3.4 特征相关性分析

# 计算特征与目标变量的相关性
corrs = data.corr()
plt.figure(figsize=(12, 8))
corrs['fare_amount'].sort_values().plot.bar(color='b')
plt.title('特征与费用的相关性')
plt.xlabel('特征')
plt.ylabel('相关系数')

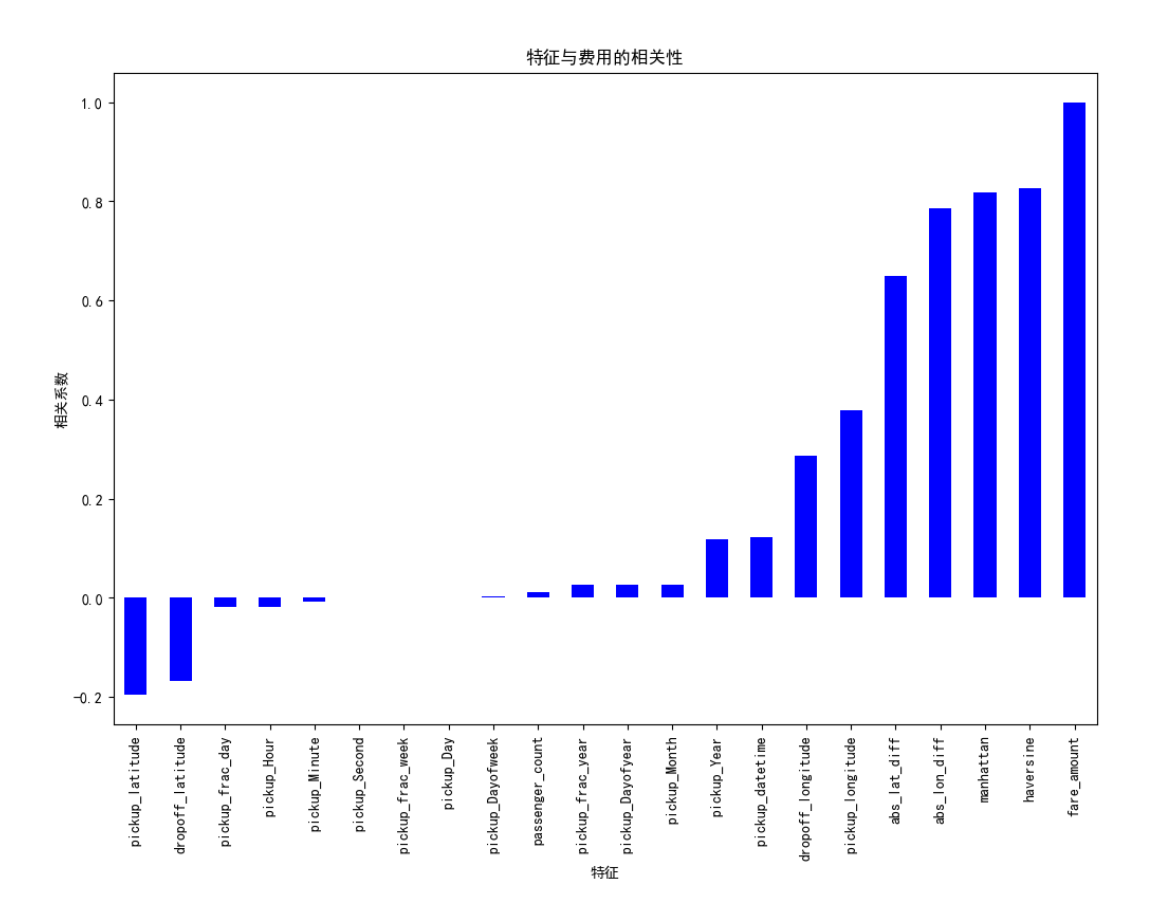
关键发现：

Haversine距离与费用的相关性最强（~0.8）
空间差异特征有中等相关性
时间特征相关性较弱但仍有一定影响

🤖 四、机器学习建模

4.1 数据分割

# 添加费用分箱用于分层抽样
data['fare-bin'] = pd.cut(data['fare_amount'], bins=list(range(0, 50, 5))).astype(str)

# 分层分割训练集和验证集
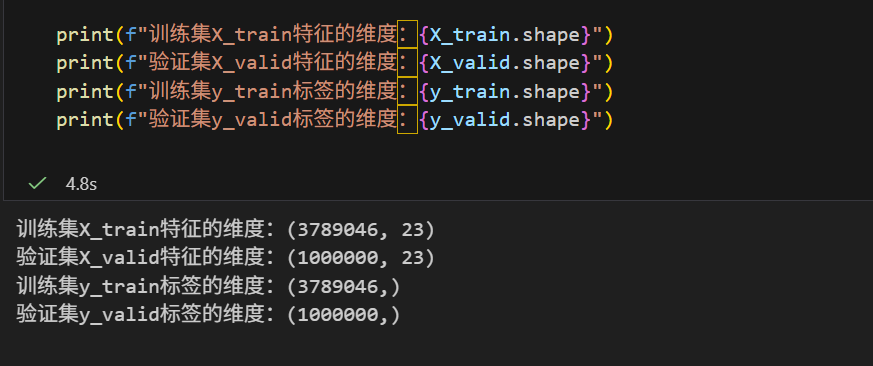
X_train, X_valid, y_train, y_valid = train_test_split(
    data, np.array(data['fare_amount']), 
    stratify=data['fare-bin'],
    random_state=100, 
    test_size=1_000_000
)

4.2 基线模型：简单线性回归

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 基础特征集
basic_features = ['abs_lat_diff', 'abs_lon_diff', 'passenger_count']

# 训练线性回归
lr = LinearRegression()
lr.fit(X_train[basic_features], y_train)

# 评估函数

def evaluate(model, features, X_train, X_valid, y_train, y_valid):
    train_pred = model.predict(X_train[features])
    valid_pred = model.predict(X_valid[features])
    
    train_rmse = np.sqrt(mean_squared_error(y_train, train_pred))
    valid_rmse = np.sqrt(mean_squared_error(y_valid, valid_pred))

    # 这里计算百分比误差
    train_ape = abs((y_train - train_pred) / y_train)
    valid_ape = abs((y_valid - valid_pred) / y_valid)
    
    # 将0分母的设置为0 
    train_ape[train_ape == np.inf] = 0
    train_ape[train_ape == -np.inf] = 0
    valid_ape[valid_ape == np.inf] = 0
    valid_ape[valid_ape == -np.inf] = 0
    
    train_mape = 100 * np.mean(train_ape)
    valid_mape = 100 * np.mean(valid_ape)
    
    print(f'训练集RMSE: {train_rmse:.2f}')
    print(f'验证集RMSE: {valid_rmse:.2f}')
    print(f'训练集平均绝对百分比误差: {train_mape:.2f}%')
    print(f'验证集平均绝对百分比误差: {valid_mape:.2f}%')
    return train_rmse,train_mape, valid_rmse,valid_mape

# 评估基线模型
train_rmse, valid_rmse = evaluate(lr, basic_features, X_train, X_valid, y_train, y_valid)

线性回归结果：

训练集RMSE: 5.33
验证集RMSE: 5.40
平均绝对百分比误差: 28.07%

4.3 随机森林模型

from sklearn.ensemble import RandomForestRegressor

# 定义特征集合
features = ['haversine', 'abs_lat_diff', 'abs_lon_diff', 'passenger_count',
            'pickup_latitude', 'pickup_longitude', 
            'dropoff_latitude', 'dropoff_longitude',
            'pickup_frac_day', 'pickup_frac_week', 
            'pickup_frac_year', 'pickup_Elapsed']

# 训练随机森林
rf = RandomForestRegressor(
    n_estimators=20, 
    max_depth=20,
    n_jobs=-1,
    random_state=100
)
rf.fit(X_train[features], y_train)

# 评估随机森林
rf_train_rmse, rf_valid_rmse = evaluate(rf, features, X_train, X_valid, y_train, y_valid)

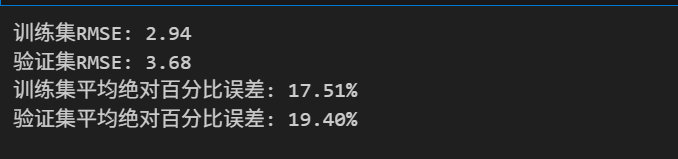
随机森林结果：

训练集RMSE: 2.94
验证集RMSE: 3.68
平均绝对百分比误差: 18.46%

4.4 模型对比分析

模型	训练集RMSE	验证集RMSE	MAPE	关键特点
线性回归	5.33	5.40	28.07%	简单可解释
随机森林	2.94	3.68	18.46%	最佳性能

4.5 特征重要性分析

# 提取特征重要性
feature_importance = pd.DataFrame({
    'feature': features,
    'importance': rf.feature_importances_
}).sort_values('importance', ascending=False)

# 可视化特征重要性
plt.figure(figsize=(10, 6))
plt.barh(feature_importance['feature'], feature_importance['importance'])
plt.xlabel('特征重要性')
plt.title('随机森林特征重要性排序')
plt.gca().invert_yaxis()

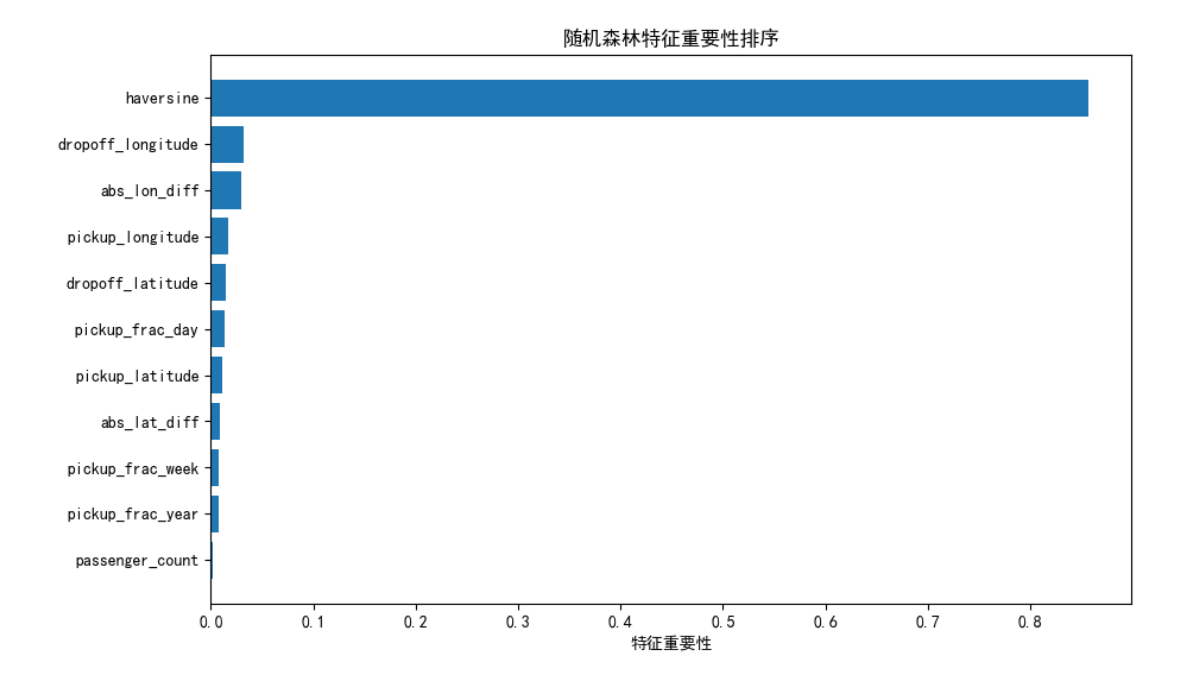
关键发现：

Haversine距离是最重要的特征（重要性>80%）
空间坐标特征有一定重要性
时间特征重要性较低但仍有贡献

4.6 超参数调优

from sklearn.model_selection import RandomizedSearchCV

# 超参数网格
param_grid = {
    'n_estimators': np.linspace(10, 100).astype(int),
    'max_depth': [None] + list(np.linspace(5, 30).astype(int)),
    'max_features': ['auto', 'sqrt', None] + list(np.arange(0.5, 1, 0.1)),
    'min_samples_split': [2, 5, 10],
}

# 随机搜索
rs = RandomizedSearchCV(
    RandomForestRegressor(random_state=100),
    param_grid,
    n_jobs=-1,
    scoring='neg_mean_absolute_error',
    cv=3,
    n_iter=50,
    verbose=1,
    random_state=100
)

# 在小样本上搜索最佳参数
tune_data = data.sample(100_000, random_state=100)
rs.fit(tune_data[features], tune_data['fare_amount'])

# 最佳模型
best_rf = rs.best_estimator_
print(f"最佳参数: {rs.best_params_}")
print(f"最佳分数: {-rs.best_score_:.2f}")