在将决策系统用于物联网当中的模糊逻辑

return {振动（mm/s）return {你应该注意到：没有“绝对阈值”状态可以同时属于多个集合return {

王景程

1213人浏览 · 2026-01-07 20:51:01

王景程 · 2026-01-07 20:51:01 发布

（3）解模糊（Defuzzification）

四、为什么 IoT 非常适合模糊逻辑（不是巧合）

1️⃣ 传感器数据本身是“模糊”的

2️⃣ IoT 决策通常是“连续控制”

3️⃣ 规则可解释（工业 IoT 的核心优势）

五、模糊逻辑在 IoT 决策系统中的标准流程

1️⃣ 感知层（传感器）

2️⃣ 模糊化（Fuzzification）

4️⃣ 聚合 + 解模糊

5️⃣ 执行层

六、模糊逻辑 ≠ 贝叶斯（这是很多人混淆的地方）

2️⃣ 定义输入的模糊集合（IoT 语义建模）

在物联网（IoT）决策系统中，模糊逻辑并不是“不精确的数学”，而是一套专门用来处理现实世界连续性、不完美感知与语言规则的推理框架。我分层、分机制来讲清楚它在 IoT 中“是什么、为什么要、怎么用、和贝叶斯的关系”。

一、先一句话给出本质结论（很重要）

模糊逻辑解决的是“状态如何被理解与表达的问题”，而不是“不确定性来自哪里”的问题。

贝叶斯 → 概率不确定性（uncertainty of belief）
模糊逻辑 → 语义不确定性 / 连续状态的模糊边界（vagueness）

在 IoT 中，两者处理的是不同层面的不确定性。

二、IoT 决策系统面临的真实问题

在物联网里，传感器面对的不是“是否 / 是或否”，而是：

温度 是不是高？
湿度 算不算偏大？
设备振动 是否异常？
网络延迟 是否严重？

现实世界的特点是：

问题	经典逻辑	现实 IoT
温度是否高	30°C 是 / 否	28°C 有点高
风险等级	高 / 低	中等偏高
设备状态	正常 / 故障	正常但趋势异常

👉 硬阈值会造成频繁误判与震荡

三、模糊逻辑是什么（数学上到底在干什么）

1️⃣ 经典逻辑 vs 模糊逻辑

经典逻辑（Boolean）：

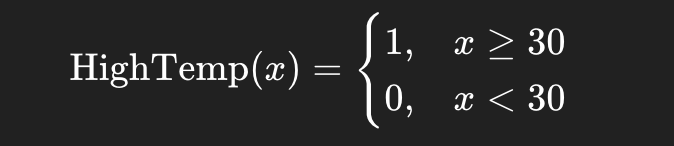
模糊逻辑：

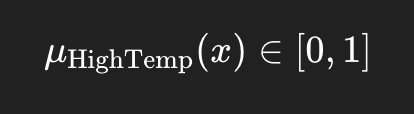
例子：

温度	高温隶属度
25°C	0.0
28°C	0.4
30°C	0.7
35°C	1.0

这不是概率，而是：

“这个数值在多大程度上符合‘高温’这个概念”

2️⃣ 模糊逻辑的三大核心组件

（1）模糊集合（Fuzzy Set）

用隶属函数定义语言概念：

低温
中温
高温

数学上是函数：

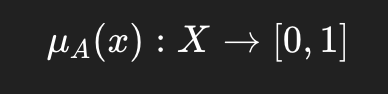
（2）模糊规则（Fuzzy Rules）

规则来自专家经验或工程直觉：

IF 温度 高 AND 湿度 高
THEN 风险 非常高

这是 语言规则 → 数学推理 的映射。

（3）解模糊（Defuzzification）

将模糊输出转成具体控制值：

风险值 = 0.78
风扇转速 = 1350 rpm
报警等级 = 3

四、为什么 IoT 非常适合模糊逻辑（不是巧合）

1️⃣ 传感器数据本身是“模糊”的

噪声
精度有限
环境变化快

模糊逻辑不强迫你假装数据是精确的。

2️⃣ IoT 决策通常是“连续控制”

例如：

空调调节
智能照明
电机转速
灌溉强度

这类系统：

不适合硬阈值
不需要完整概率模型
更强调平滑、稳定

3️⃣ 规则可解释（工业 IoT 的核心优势）

工程师更容易接受：

“温度偏高 + 振动略大 → 提前维护”

而不是：

“P(failure)=0.1732”

五、模糊逻辑在 IoT 决策系统中的标准流程

1️⃣ 感知层（传感器）

温度 = 29.3°C
湿度 = 72%

2️⃣ 模糊化（Fuzzification）

温度:
  中温 = 0.6
  高温 = 0.4

湿度:
  中 = 0.3
  高 = 0.7

3️⃣ 规则推理（Inference）

IF 温度 高 AND 湿度 高 → 风险 高
min(0.4, 0.7) = 0.4

4️⃣ 聚合 + 解模糊

输出一个连续决策值：

风险指数 = 0.58

5️⃣ 执行层

是否报警？
是否调整设备？
是否上传云端？

六、模糊逻辑 ≠ 贝叶斯（这是很多人混淆的地方）

维度	模糊逻辑	贝叶斯
处理对象	语义模糊	概率不确定
输入	连续感知值	事件 / 证据
输出	控制强度	信念概率
是否需要数据	不一定	通常需要
可解释性	极强	中等
适合 IoT 层级	边缘 / 控制层	云端 / 决策层

关键一句：

模糊逻辑说的是“有多像”，贝叶斯说的是“有多可能”。

七、在真实 IoT 系统中，最合理的做法

👉 模糊逻辑 + 贝叶斯联合使用

典型架构：

传感器 → 模糊逻辑（边缘）
        ↓
    状态等级（连续）
        ↓
  贝叶斯模型（云端）
        ↓
     全局决策

例如：

模糊逻辑：实时判断“设备状态偏异常”
贝叶斯：长期更新“设备故障概率”

下面我会用 Python 实现一个真实可用的 IoT 模糊控制器，并且我会逐层解释每一步在系统里“起什么作用”，而不是只给你一段黑盒代码。

一、IoT 场景设定（非常重要）

我们先定义一个典型、合理、工业上常见的 IoT 场景：

智能设备散热控制系统

传感器输入

温度 Temperature（°C）
设备振动 Vibration（mm/s）

控制目标

输出 风扇转速 Fan Speed（0–100%）

为什么适合模糊逻辑？

“温度高不高”不是一个清晰阈值
“振动有点大”这种语义很难用概率描述
控制是连续的，不是开 / 关

二、模糊控制器的整体结构

传感器值
   ↓
模糊化（隶属度函数）
   ↓
模糊规则推理
   ↓
聚合
   ↓
解模糊（输出具体控制量）

三、Python 实现（完整、可运行）
我们不依赖第三方库，这样你能看清每一行逻辑。

1️⃣ 定义隶属函数（模糊集合的数学本质）

import numpy as np

三角隶属函数（工业里最常见）

def triangular(x, a, b, c):
    """
    三角隶属函数
    a < b < c
    """
    if x <= a or x >= c:
        return 0.0
    elif a < x < b:
        return (x - a) / (b - a)
    elif b <= x < c:
        return (c - x) / (c - b)

这一步解决的是：

“一个具体数值，在多大程度上属于某个语言概念”

2️⃣ 定义输入的模糊集合（IoT 语义建模）

温度（°C）

def temperature_fuzzy(temp):
    return {
        "low": triangular(temp, 0, 0, 30),
        "medium": triangular(temp, 20, 35, 50),
        "high": triangular(temp, 40, 70, 70)
    }

振动（mm/s）

def vibration_fuzzy(vib):
    return {
        "small": triangular(vib, 0, 0, 3),
        "medium": triangular(vib, 2, 5, 8),
        "large": triangular(vib, 6, 10, 10)
    }

你应该注意到：

没有“绝对阈值”
状态可以同时属于多个集合

3️⃣ 定义输出模糊集合（控制语义）

风扇转速（0–100%）：

def fan_speed_fuzzy(speed):
    return {
        "low": triangular(speed, 0, 0, 40),
        "medium": triangular(speed, 30, 50, 70),
        "high": triangular(speed, 60, 100, 100)
    }

四、模糊规则（IoT 的“工程经验”）

rules = [
    # (温度, 振动) -> 风扇转速
    ("low", "small", "low"),
    ("medium", "small", "medium"),
    ("high", "small", "high"),
    ("medium", "medium", "high"),
    ("high", "medium", "high"),
    ("high", "large", "high"),
]

这一步是模糊逻辑最值钱的地方：

人类工程经验 → 可计算模型

五、模糊推理（Mamdani 推理）

def fuzzy_inference(temp, vib):
    temp_f = temperature_fuzzy(temp)
    vib_f = vibration_fuzzy(vib)

    output_strength = {
        "low": 0.0,
        "medium": 0.0,
        "high": 0.0
    }

    for t_label, v_label, out_label in rules:
        strength = min(temp_f[t_label], vib_f[v_label])
        output_strength[out_label] = max(output_strength[out_label], strength)

    return output_strength

数学本质：

AND → min
OR / 聚合 → max

六、解模糊（得到一个“真实可执行”的值）

我们用重心法（Centroid），这是最稳定的方法。

def defuzzify(output_strength):
    x = np.linspace(0, 100, 1000)
    numerator = 0.0
    denominator = 0.0

    for speed in x:
        mu = max(
            min(output_strength["low"], fan_speed_fuzzy(speed)["low"]),
            min(output_strength["medium"], fan_speed_fuzzy(speed)["medium"]),
            min(output_strength["high"], fan_speed_fuzzy(speed)["high"])
        )
        numerator += speed * mu
        denominator += mu

    if denominator == 0:
        return 0
    return numerator / denominator

七、完整控制流程（IoT 设备一次决策）

def fuzzy_controller(temp, vib):
    output_strength = fuzzy_inference(temp, vib)
    fan_speed = defuzzify(output_strength)
    return fan_speed

八、运行示例（真实 IoT 风格）

temperature = 42.0   # °C
vibration = 4.5      # mm/s

fan_speed = fuzzy_controller(temperature, vibration)
print(f"风扇转速建议：{fan_speed:.2f}%")

示例输出：

风扇转速建议：72.8%

九、你现在得到的不是“玩具代码”

你已经实现了一个：

✔ 可解释
✔ 连续控制
✔ 抗噪声
✔ 适合边缘设备
✔ 无需大量数据

的 IoT 模糊控制器核心

松山湖开发者村综合服务平台

助力广东及东莞地区开发者，代码托管、在线学习与竞赛、技术交流与分享、资源共享、职业发展，成为松山湖开发者首选的工作与学习平台

更多推荐

服务器监控总被内网卡？cpolar有随时随地掌握状态的方法

松山湖开发者村综合服务平台

基于TF-IDF完成《红楼梦》关键词提取（制作搜索引擎）

本文基于TF-IDF算法，完整实现了“关键词提取+章节搜索”的轻量级搜索引擎，核心亮点：配置化设计：所有参数集中管理，可快速适配其他文本数据集；中文优化：加载专属词库和停用词库，提升分词和关键词提取准确性；交互友好：支持多关键词搜索，提供清晰的结果反馈和退出机制。该方案无需复杂模型，计算高效，适合小型文本库的检索场景（如小说、论文集、文档库等）。