线性回归是机器学习中最基础、最常用的算法之一，核心作用是 “建模变量间的线性关系”，比如用广告投入预测销售额、用学习时长预测考试成绩。它原理简单、可解释性强，是解决回归类问题的 “入门首选”，工作中掌握这一章的核心内容，能应对 80% 的连续值预测场景。

一、核心逻辑：线性回归到底在做什么？

线性回归的本质是找一条最优直线（或超平面），拟合自变量和因变量的线性关系，最终用这条直线做预测。

• 简单理解：比如 “销售额 = 0.8× 广告投入 + 5”，就是通过数据找到 “0.8” 和 “5” 这两个参数，让直线尽可能贴近所有真实数据点。
• 核心目标：最小化 “预测值与真实值的误差”，让模型预测更准。

二、基本概念：

1. 一元线性回归：只有一个自变量（比如仅用 “学习时长” 预测 “成绩”），公式：y=β0​+β1​x（β0​是截距，β1​是系数）。

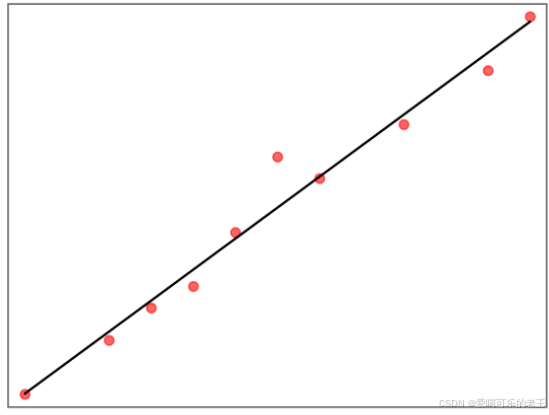
1. 多元线性回归：有多个自变量（比如用 “TV 广告 + 广播广告 + 报纸广告” 预测 “销售额”），公式：y=β0​+β1​x1​+β2​x2​+...+βn​xn​。

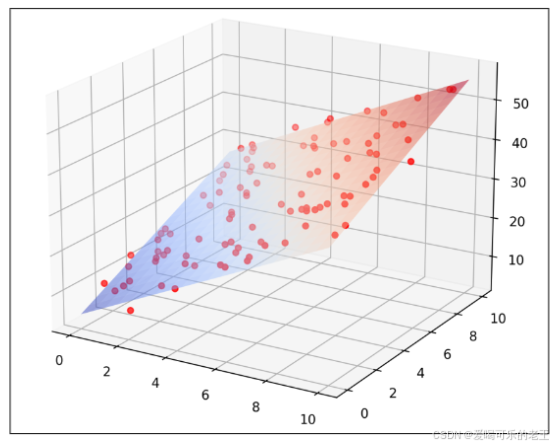
1. 系数（β）：表示自变量对因变量的影响程度。比如β1​=2.8，意味着 “学习时长每增加 1 小时，成绩平均增加 2.8 分”。
2. 损失函数：衡量预测误差的标准，工作中最常用均方误差（MSE） —— 把每个误差平方后求平均，能放大极端误差（比如预测错 10 万和错 1 万，平方后差距更明显）。

三、常用的 2 种模型求解方法

线性回归的核心是找到最优参数β，实际工作中主要用两种方法，各有适用场景：

1. 正规方程法（解析法）：直接算结果，简单高效

• 原理：通过数学公式直接求解参数，不用迭代，一步到位。
• 适用场景：特征数量少（比如≤1000），数据量不大（比如≤10 万条）。
• 优点：代码简单、结果精确，不用调参。
• 缺点：特征太多时，计算量会急剧增加，效率变低。
• Python 代码示例（直接调用 sklearn）：

from sklearn.linear_model import LinearRegression
import numpy as np

# 自变量（广告投入：TV、广播、报纸，单位：千元）
X = np.array([[10, 2, 1], [20, 3, 2], [30, 5, 3]])
# 因变量（销售额，单位：百万元）
y = np.array([5, 8, 12])

# 初始化模型，拟合数据（自动用正规方程法求解）
model = LinearRegression()
model.fit(X, y)

# 查看系数（每个自变量对销售额的影响）
print("系数：", model.coef_)  # 输出：[0.3 0.5 0.1]（TV影响最大）
print("截距：", model.intercept_)  # 输出：1.2
# 预测（投入TV=25，广播=4，报纸=2，销售额是多少？）
print("预测销售额：", model.predict([[25, 4, 2]])[0])  # 输出：约9.9百万元

2. 梯度下降法：迭代求最优，适配大数据

• 原理：像 “下山” 一样，沿着误差减少最快的方向（负梯度），一步步调整参数，直到误差最小。
• 适用场景：特征数量多（比如≥1 万）、数据量大（比如≥100 万条），正规方程法算不动的时候。
• 关键参数：学习率（α） —— 步长大小（太大容易跳过最优解，太小收敛太慢）。
• 梯度下降法常见问题

1. 特征缩放：通常需要提前对特征进行缩放（如标准化或归一化），以加快收敛速度。
2. 局部极小值、鞍点问题：可能陷入局部极小值（非全局最优解），或遇到鞍点（梯度为零但非极值点）。
   解决方案：使用动量（Momentum）、自适应优化器（如Adam）或二阶方法（如牛顿法）。
3. 常见类型：小批量梯度下降（Mini-batch GD）：工作中最常用，每次用一小批数据（比如 32/64 条）计算梯度，平衡速度和稳定性。

• Python 代码示例（随机梯度下降）：

from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

# 数据标准化（梯度下降必须做，否则收敛慢）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 初始化模型（损失函数用均方误差，学习率0.1）
sgd_model = SGDRegressor(loss="squared_error", eta0=0.1, max_iter=1000)
sgd_model.fit(X_scaled, y)

# 预测（注意：输入也要标准化）
X_test_scaled = scaler.transform([[25, 4, 2]])
print("SGD预测销售额：", sgd_model.predict(X_test_scaled)[0])  # 结果和正规方程法接近

四、工作实战技巧：避坑 + 优化

1. 数据预处理是前提：
   • 必须处理缺失值、异常值（比如销售额突然出现 1000 万，要替换或剔除），否则会严重影响拟合效果。
   • 特征要标准化 / 归一化：尤其是用梯度下降时，避免因特征量纲差异（比如身高用米、体重用千克）导致收敛慢。
2. 避免过拟合：
   • 线性回归容易因特征过多出现过拟合（训练集预测准，测试集不准），解决方法：
     • 用 L2 正则化（岭回归）：惩罚过大的参数，让模型更稳健。
     • 筛选有用特征：比如用相关系数剔除和因变量无关的特征。
3. 模型评估看 3 个指标：
   • 均方根误差（RMSE）：直观反映误差大小（和因变量单位一致，比如销售额误差 5 万元）。
   • 决定系数（R²）：看模型解释能力，越接近 1 越好（比如 R²=0.8，说明 80% 的销售额变化能被广告投入解释）。
4. 适用场景速记：
   • 适合：预测连续值（销售额、温度、产量）、需要解释变量影响（比如 “TV 广告每多花 1 千，销售额多赚 8 百”）。
   • 不适合：变量间是非线性关系（比如 “学习时长超过 10 小时后，成绩不再提升”）。

（注）线性回归案例案例