【数学 高度等数】函数与极限
本文探讨了周期函数、极限与有界性等数学概念。首先分析了一个不存在最小周期的特殊周期函数例子,该函数在有理数和无理数点取值不同。接着讨论了函数极限的定义及其与有界性的关系,指出有界函数不一定存在极限。在数列极限部分,给出了收敛数列的定义及其界的概念。随后详细阐述了无穷小的定义、运算规则及极限的四则运算法则。文章最后提供了相关学习资源推荐,包括算法资料、视频课程和测试环境说明。全文以严谨的数学语言呈现
本文涉及知识点
预习
指数函数
f(x)= a x , 且 a > 0 , a ≠ 1 a^x,且a>0,a\neq 1 ax,且a>0,a=1。 1 x ≡ 1 1^x \equiv 1 1x≡1
当底数为负数、指数为非整数时,在实数范围内可能没有定义。
a − x = 1 a x , a > 0 , x ∈ R a^{-x}=\frac 1 {a^x},a>0,x\in \R a−x=ax1,a>0,x∈R
a x > 0 , a > 0 , x ∈ R a^x>0,a>0,x\in \R ax>0,a>0,x∈R
a > 0 , a x × y = ( a x ) y a>0,a^{x \times y}=(a^x)^y a>0,ax×y=(ax)y
x y = ( e ln x ) y = e y ln x , x , y ∈ R , x > 0 x^y=(e^{\ln x})^y=e^{y\ln x},x,y\in \R,x>0 xy=(elnx)y=eylnx,x,y∈R,x>0
a p q = ( a q ) p a ∈ R + , p ∈ Z , q ∈ Z + a^\frac p q=(\sqrt[q]a)^p a\in \R+,p \in \Z,q \in \Z+ aqp=(qa)pa∈R+,p∈Z,q∈Z+
q ∈ Z + , 0 < a < 1 → 0 < a q < 1 ; a > 1 → a q > 1 q \in \Z+,0<a<1 \to 0<a^q <1;a>1 \to a^q>1 q∈Z+,0<a<1→0<aq<1;a>1→aq>1
q ∈ Z + , 令 x = a q → x q = a 。 0 < x < 1 , 则 0 < a < 1 ; x > 1 ,则 a > 1 q\in\Z+,令x=\sqrt[q] a \to x^q=a。0<x<1,则0<a<1;x>1,则a>1 q∈Z+,令x=qa→xq=a。0<x<1,则0<a<1;x>1,则a>1
即 a> 1,a的q次方和开q次方,都大于1;0<a<1,a的q次方和开q次方都小于1。即 a > 1 , a x > 1 , x ∈ R + ; 0 < a < 1 , a x < 1 a>1,a^x>1,x\in\R+;0<a<1,a^x<1 a>1,ax>1,x∈R+;0<a<1,ax<1
对数运算
乘法: log b ( x y ) = l o g b x + l o g b y \log_b(xy)=log_bx+log_by logb(xy)=logbx+logby
除法: log b ( x y ) = l o g b x − l o g b y \log_b(\frac x y)=log_bx-log_by logb(yx)=logbx−logby
幂法则: log b x a = a l o g b x \log_b x^a=alog_b x logbxa=alogbx
换底公式: log a b = log k a log k b \log_a b= \frac {\log_k a}{\log_k b} logab=logkblogka
不存在周小周期的周期函数
周期函数: ∀ x , ∃ 正实数 L \forall x, \exist 正实数L ∀x,∃正实数Lf(x)=f(L+x)。
下述函数存在周期不存在最小周期
{ 1 x 是有理数 0 x 是无理数 \begin{cases} 1 & x是有理数 \\ 0 & x是无理数 \\ \end{cases} {10x是有理数x是无理数
有理数是可以表示为 两个整数之比(分数形式)的数。即 a b a , b ∈ Z , b ≠ 0 \frac a b a,b\in \Z,b \neq 0 baa,b∈Z,b=0。
令l = a ÷ b a \div b a÷b。
性质一:如果x( c ÷ d c \div d c÷d)是有理数,则x+l也是有理数。 a ÷ b + c ÷ d = ( a × d + c × b ) ÷ ( b × d ) a \div b + c \div d=(a\times d + c \times b)\div (b \times d) a÷b+c÷d=(a×d+c×b)÷(b×d)是有理数。
性质二:如果x是无理数,则x+l是无理数。可以用反证法证明:令l+x是无理数 c ÷ d c\div d c÷d,则x= c ÷ d − a ÷ b = ( b × c − a × d ) ÷ ( b × d ) c\div d- a\div b=(b\times c - a\times d)\div (b \times d) c÷d−a÷b=(b×c−a×d)÷(b×d)。即x也是有理数,无理数。
函数的极限与界
函数f(x)在某个去心邻域有定义,如果存在常数L,使得 ∀ ϵ , ϵ > 0 , ∃ δ \forall \epsilon,\epsilon>0 ,\exist \delta ∀ϵ,ϵ>0,∃δ。任意0 <|x-x0|< δ \delta δ,都有|f(x)-L|< ϵ \epsilon ϵ。
则称L是f(x)当x趋于x0时的极限。记作 lim x → x 0 f ( x ) \lim_{x \to x0} f(x) limx→x0f(x)
极限存在 ⟺ \iff ⟺ 左极限和右极限存在且相等。
函数f(x)在集合D上有界,即 ∀ x ∈ D \forall x\in D ∀x∈D, |f(x)|<=M。
极限存在 → \rightarrow → 局部有界。
有界函数不一定有极限
一,震荡函数,如f(x)= s i n ( 1 ÷ x ) , x ≠ 0 sin(1 \div x),x\neq 0 sin(1÷x),x=0,界是1,x趋于0时,无极限。
二,分段函数。如符合函数。
{ 1 x > 0 0 x = = 0 − 1 x < 0 \begin{cases} 1 && x>0 \\ 0 && x==0 \\ -1 && x < 0\\ \end{cases} ⎩
⎨
⎧10−1x>0x==0x<0
x趋于0时,左右极限是-1,1不等。
数列的极限与界
数列{ a n a_n an}, ∀ 正实数 ϵ , ∃ N \forall 正实数\epsilon,\exist N ∀正实数ϵ,∃N,当n > N时。
| a n − L a_n-L an−L|< ϵ \epsilon ϵ,则称数列{ a n a_n an}收敛于L,记作 lim n → ∞ a n = L \lim\limits_{n \to \infty}a_n=L n→∞liman=L或 a n → L ( x → ∞ ) a_n \to L (x \to \infty) an→L(x→∞)
数列{ a n a_n an}的界是M, ∀ n \forall n ∀n,| a n ∣ ≤ M a_n| \leq M an∣≤M
无穷小
函数无穷小的定义
x趋于 x 0 x_0 x0,f(x)的极限是0。
x趋于 ∞ \infty ∞,f(x)的极限是0。
无穷小的运算
定理一:有限个无穷小之和仍然是无穷小。x趋于 x 0 x_0 x0,f(x)的容差为 ϵ ÷ 2 \epsilon \div 2 ϵ÷2,对应的 δ 为 d 1 \delta 为d1 δ为d1;
g(x)容差为 ϵ ÷ 2 \epsilon \div 2 ϵ÷2对应的 δ \delta δ为d2。则f(x)+g(x)对应的 δ \delta δ为min(d1,d2)。
定理二:有限个无穷小的差仍然是无穷小。f(x)-g(x) ⟺ \iff ⟺f(x)+(-g(x))。
定理三:无穷小与有界量的积是无穷小。f(x)容差为 ϵ ÷ M \epsilon \div M ϵ÷M对应的 δ \delta δ为d。则
Mf(x)在 δ \delta δ为d时,Mf(x) < ϵ \epsilon ϵ。
推理一:无穷小和常数的乘积是无穷小。
推理二:无穷小的乘积是无穷小。
定理四:无穷小的线性组合是无穷小。
极限的四则运算
lim x → a f ( x ) = A , lim x → a g ( x ) = B \lim\limits_{x \to a}f(x)=A,\lim\limits_{x \to a}g(x)=B x→alimf(x)=A,x→alimg(x)=B,A和B是有限实数。
lim x → a ( f ( x ) ± g ( x ) ) = A ± B \lim\limits_{x \to a}(f(x) \pm g(x))= A \pm B x→alim(f(x)±g(x))=A±B
lim x → a ( f ( x ) . g ( x ) ) = A . B \lim\limits_{x \to a}(f(x) . g(x))= A . B x→alim(f(x).g(x))=A.B
lim x → a ( f ( x ) ÷ g ( x ) ) = A ÷ B , B ≠ 0 \lim\limits_{x \to a}(f(x) \div g(x))= A \div B,B \neq 0 x→alim(f(x)÷g(x))=A÷B,B=0
猜想:C是常数, f ( x ) C = A C f(x)^C=A^C f(x)C=AC
两个重要的极限
lim x → 0 sin x x = 1 \lim\limits_{x \to 0}\frac {\sin x}x = 1 x→0limxsinx=1
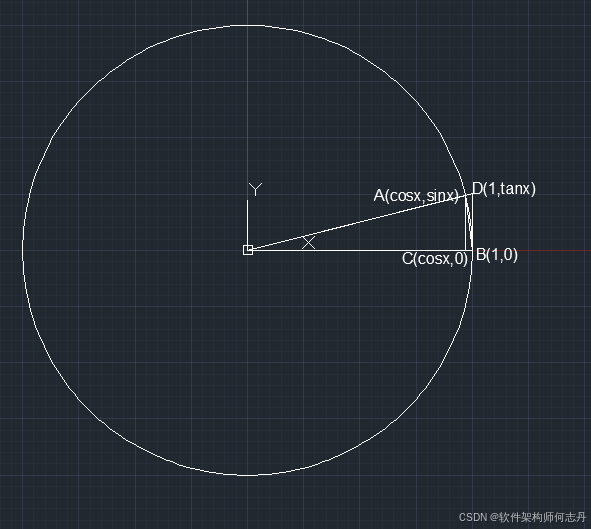
△ O A B \triangle OAB △OAB的面积是: 底 × 高 = ∣ O B ∣ ∗ ∣ A C ∣ / 2 = 1 × sin x ÷ 2 底 \times 高=|OB|*|AC|/2= 1\times \sin x\div2 底×高=∣OB∣∗∣AC∣/2=1×sinx÷2
扇形OAB的面积= 1 ÷ 2 × x × 1 × 1 = x ÷ 2 1 \div 2 \times x \times 1 \times 1=x \div 2 1÷2×x×1×1=x÷2
△ O B D \triangle OBD △OBD的面积是: 1 ∗ tan x ÷ 2 1* \tan x \div 2 1∗tanx÷2
三者的面积依次增大,故 sin x < x < tan x \sin x < x < \tan x sinx<x<tanx
lim x → 0 sin x sin x = 1 \lim\limits_{x \to 0}\frac {\sin x} {\sin x}=1 x→0limsinxsinx=1
lim x → 0 tan x sin x = cos x = 1 \lim\limits _{x \to 0}\frac{\tan x}{\sin x}=\cos x =1 x→0limsinxtanx=cosx=1
根据夹逼准则,因为: sin x ÷ sin x < x ÷ sin x < tan x ÷ sin x \sin x \div \sin x < x \div \sin x < \tan x \div \sin x sinx÷sinx<x÷sinx<tanx÷sinx。
所以: lim x → 0 x sin x = 1 \lim\limits_{x \to 0}\frac x {\sin x} = 1 x→0limsinxx=1
lim x → 0 sin x x = lim 1 ÷ lim x sin x \lim\limits_{x \to 0}\frac {\sin x}x=\lim 1 \div \lim \frac x {\sin x} x→0limxsinx=lim1÷limsinxx
常见推论
| 三角函数的等价极限 | ||
|---|---|---|
| sinx tan x arcsin x arctan x | x | 等价无穷小 |
| 1 − cos x 1-\cos x 1−cosx | x 2 ÷ 2 x^2\div 2 x2÷2 | 等价无穷小 |
| 1 − sec x 1-\sec x 1−secx | − x 2 ÷ 2 -x^2\div 2 −x2÷2 | 等价无穷小 |
lim x → 0 tan x ÷ x = sin x ÷ x ÷ cos x = 1 ÷ cos x = 1 \lim\limits_{x \to 0}\tan x \div x=\sin x \div x \div \cos x=1 \div \cos x=1 x→0limtanx÷x=sinx÷x÷cosx=1÷cosx=1
lim x → 0 ( 1 − cos x ) ÷ x 2 = ( 1 − cos x ) ( 1 + cos x ) x 2 ( 1 + cos x ) = 1 − cos 2 x x 2 ( 1 + cos x ) = sin 2 x x 2 ( 1 + cos x ) = 1 ÷ ( 1 + c o s x ) = 1 2 \lim\limits_{x \to 0}(1-\cos x)\div x^2=\frac {(1-\cos x)(1+\cos x)}{x^2(1+\cos x)}=\frac{1-\cos^2x}{x^2(1+\cos x)}=\frac {\sin^2x}{x^2 (1+\cos x)}=1 \div (1+cosx)=\frac 1 2 x→0lim(1−cosx)÷x2=x2(1+cosx)(1−cosx)(1+cosx)=x2(1+cosx)1−cos2x=x2(1+cosx)sin2x=1÷(1+cosx)=21
lim x → 0 arcsin x ÷ x = 1 \lim\limits_{x \to 0}\arcsin x \div x=1 x→0limarcsinx÷x=1证明过程如下:
令 x = sin t → arcsin x = t x = \sin t \to \arcsin x =t x=sint→arcsinx=t
则 lim x → 0 arcsin x ÷ x = lim t → 0 t ÷ sin t = 1 \lim\limits_{x \to 0}\arcsin x \div x=\lim\limits_{t \to 0}t\div \sin t=1 x→0limarcsinx÷x=t→0limt÷sint=1
lim x → 0 arctan x ÷ x = 1 \lim\limits_{x \to 0}\arctan x \div x=1 x→0limarctanx÷x=1
lim x → 0 1 − sec x x 2 = cos x − 1 cos x ÷ x 2 = − 1 ÷ 2 ÷ c o s x = − 1 ÷ 2 \lim\limits_{x \to 0} \frac{1-\sec x}{x^2}=\frac {\cos x -1}{\cos x}\div x^2=-1\div 2 \div cosx=-1\div 2 x→0limx21−secx=cosxcosx−1÷x2=−1÷2÷cosx=−1÷2
自然对数的底
lim x → ∞ ( 1 + x x ) x = lim x → ∞ ( 1 + 1 x ) x = e \lim\limits_{x \to \infty}(\frac{1+x}x)^x =\lim\limits_{x \to \infty}(1+\frac 1 x)^x=e x→∞lim(x1+x)x=x→∞lim(1+x1)x=e
( 1 + 1 n ) n = ∑ i : 0 n C n 0 1 n − i ( 1 n ) i (1+\frac 1 n )^n=\sum_{i:0}^n C_n^01^{n-i}(\frac 1 n)^i (1+n1)n=∑i:0nCn01n−i(n1)i
a n a_n an第i项 = n × n − 1 × ⋯ n − ( n − i ) + 1 ( n ) i × i ! < 1 i ! \frac {n \times n-1 \times \cdots n-(n-i)+1} {(n)^i \times i!} < \frac 1 {i!} (n)i×i!n×n−1×⋯n−(n−i)+1<i!1
第0到第2项分别是: 1 + 1 + ( 1 − 1 2 ) 1+1+(1-\frac 1 2) 1+1+(1−21)
第i项< 1 ( i − 2 ) ! ( 1 i − 1 − 1 i ) < 1 i − 1 − 1 i \frac 1 {(i-2)!}(\frac 1 {i-1} -\frac 1 i)<\frac 1 {i-1} -\frac 1 i (i−2)!1(i−11−i1)<i−11−i1,i > 2
故其和<3,即有上界。
a n a_n an第i项 = ( 1 − 1 n ) ( 1 − 2 n ) ⋯ ÷ i ! (1-\frac 1 n)(1-\frac 2 n ) \dots \div i! (1−n1)(1−n2)⋯÷i!
a n + 1 a_{n+1} an+1第i项 = ( 1 − 1 n + 1 ) ( 1 − 2 n + 1 ) ⋯ ÷ i ! (1-\frac 1 {n+1})(1-\frac 2 {n+1} ) \dots \div i! (1−n+11)(1−n+12)⋯÷i!
显然 a n a_n an的第i都小于 a n + 1 a_{n+1} an+1项, a n + 1 a_{n+1} an+1还多第n+1项,故 a n + 1 > a n a_{n+1} > a_n an+1>an。故数列 a n a_n an单调。
单调有界 = > => =>有极限。
e的定义 = lim x → ∞ ( 1 + 1 n ) n = e ≈ 2.78 , n ∈ Z =\lim\limits_{x \to \infty}(1+\frac 1 n)^n=e \approx 2.78,n \in \Z =x→∞lim(1+n1)n=e≈2.78,n∈Z
下面利用夹逼准则来证明, x ∈ R x \in \R x∈R。
n = ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ f ( x ) = ( 1 + 1 n ) n , g ( x ) = ( 1 + 1 n + 1 ) n + 1 f(x)=(1 + \frac 1 n)^n,g(x)= (1+ \frac 1 {n+1})^{n+1} f(x)=(1+n1)n,g(x)=(1+n+11)n+1
f ( x ) ≤ ( 1 + 1 x ) x < g ( x ) f(x) \le (1+ \frac 1 x)^x< g(x) f(x)≤(1+x1)x<g(x),而f(x)和g(x)的极限是e,故 x ∈ R \in \R ∈R,其极限也是e。
等价形式: lim t → 0 ( 1 + t ) 1 t = e \lim\limits_{t \to 0}(1+t)^ \frac 1 t=e t→0lim(1+t)t1=e
更一般形式: lim x → ∞ ( 1 + k x ) x = e k \lim\limits_{x \to \infty}(1+\frac k x)^x=e^k x→∞lim(1+xk)x=ek
推导导数
( a x ) ′ = a x ln a → ( e x ) ′ = e x (a^x)'=a^x\ln a \to (e^x)'=e^x (ax)′=axlna→(ex)′=ex 证明比较复杂,本章不证明。
lim ( 1 + k x ) x = lim [ ( 1 + 1 x ÷ k ) x ÷ k ] k = e k \lim\limits (1+\frac k x)^x=\lim\limits [(1+ \frac 1 {x \div k})^{x \div k}]^k=e^k lim(1+xk)x=lim[(1+x÷k1)x÷k]k=ek
推论
等价形式,两边取自然对数:
左边 = l n ( 1 + x ) 1 x = ln ( 1 + x ) x =ln(1+x)^\frac 1 x=\frac {\ln(1+x)} x =ln(1+x)x1=xln(1+x),右式子=1 即 = ln ( 1 + x ) x = 1 =\frac {\ln(1+x)} x=1 =xln(1+x)=1推论一
t = e x − 1 → x = l n ( t + 1 ) t=e^x-1 \to x=ln(t+1) t=ex−1→x=ln(t+1)
推论一: ln ( t + 1 ) t = x e x − 1 = 1 \frac {\ln(t+1)} t = \frac x {e^x-1}=1 tln(t+1)=ex−1x=1 推论二
等价(~)无穷小
e x ln a = ( e ln a ) x = a x e^{x\ln a}=(e^{\ln a})^x=a^x exlna=(elna)x=ax
→ a x − 1 = e x ln a − 1 \to a^x-1=e^{x\ln a}-1 →ax−1=exlna−1
令 u = x ln a , e x ln a − 1 = e u − 1 = u = x ln a u=x \ln a,e^{x\ln a}-1=e^u-1=u=x \ln a u=xlna,exlna−1=eu−1=u=xlna
→ a x − 1 \to a^x-1 →ax−1 ~ x ln a x \ln a xlna x → 0 , a > 0 , a ≠ 1 x\to 0,a >0,a\neq 1 x→0,a>0,a=1
( 1 + x ) a = ( e x ) a = e x a (1+x)^a=(e^x)^a=e^{xa} (1+x)a=(ex)a=exa u=xa,根据 e u = 1 + u e^u=1+u eu=1+u
e x a = 1 + a x e^{xa}=1+ax exa=1+ax
即: ( 1 + x ) a = 1 + a x (1+x)^a=1+ax (1+x)a=1+ax
即 ( 1 + x ) a − 1 ∼ a x (1+x)^a-1 \sim ax (1+x)a−1∼ax
| 指数和对数 | ||
|---|---|---|
| lim x → ∞ ( 1 + 1 x ) x \lim\limits_{x \to \infty}(1+\frac 1 x)^x x→∞lim(1+x1)x | e | 等价无穷小 |
| lim x → 0 ( 1 + x ) 1 x \lim\limits_{x \to 0}(1+x)^{\frac 1 x} x→0lim(1+x)x1 | e | 等价无穷小 |
| lim x → 0 ln ( 1 + x ) \lim\limits_{x \to 0}\ln(1+x) x→0limln(1+x) | x | 等价无穷小 |
| lim x → 0 e x − 1 \lim\limits_{x \to 0}e^x-1 x→0limex−1 | x | 等价无穷小 |
| lim x → 0 a x − 1 \lim\limits_{x \to 0}a^x-1 x→0limax−1 | x ln a x\ln a xlna | 等价无穷小,a>0, a ≠ 1 a\neq 1 a=1 |
定理
α ∼ α ′ , β ∼ β ′ , lim α ′ β ′ 存在 \alpha \sim \alpha ',\beta \sim \beta ',\lim\limits \frac {\alpha'}{\beta'}存在 α∼α′,β∼β′,limβ′α′存在,则 lim α β = lim α ′ β ′ \lim\limits \frac \alpha \beta=\lim\limits \frac {\alpha'}{\beta'} limβα=limβ′α′
间断点类型
左右极限都存在
可去间断点(Removable Discontinuity)
左右极限相等,函数无定义或函数值相等。
一, { 1 x = = 0 x o t h e r \begin{cases} 1 && x==0\\ x && other \\ \end{cases} {1xx==0other
x → 0 x \to 0 x→0,左右极限是0,函数值是1。
二,f(x)= sin x x , x → 0 ,函数无定义,其极限是 1 \frac {\sin x} x,x \to 0,函数无定义,其极限是1 xsinx,x→0,函数无定义,其极限是1。
跳跃间断点(Jump Discontinuity)
左右极限都存在,但不等。
如符合函数:
{ 1 x > 0 0 x = = 0 − 1 x < 0 \begin{cases} 1 && x >0 \\ 0 && x == 0 \\ -1 && x < 0 \\ \end{cases} ⎩
⎨
⎧10−1x>0x==0x<0
x → 0 x \to 0 x→0是,左极限-1,右极限1。
如:绝对值函数:f(x)=|x|。
取整函数也是。
第二类间断点
至少一个极限不存在。
无穷间断点
至少一个极限是无穷。
f(x)= 1 x , x → 0 \frac 1 x,x \to 0 x1,x→0,左右极限是 − ∞ , + ∞ -\infty,+\infty −∞,+∞。
f(x)= tan x , x → π ÷ 2 \tan x,x \to \pi \div 2 tanx,x→π÷2,左右极限是 + ∞ +\infty +∞
振荡间断点(Oscillatory Discontinuity)
定义:当 x → 0 x \to 0 x→0时,函数值无限振荡,没有确定的极限。
{ 1 x = = 0 sin ( 1 ÷ x ) o t h e r \begin{cases} 1 && x==0\\ \sin(1 \div x) && other \end{cases} {1sin(1÷x)x==0other
左右极限在[-1,1]直接震荡。
其它第二类点
不赘述。
区间连续函数的性质
设函数f(x)在闭区间[a,b]上有定义,如果在(a,b)内每一点连续,在a右连续,在b左连续,则称f(x)在[a,b]连续。
性质一:有界性定理:如果 f ∈ C [ a , b ] 连续,则 f 在 [ a , b ] 有界。即存在常数 M > 0 ,使得 ∣ f ( x ) ∣ ≤ M , ∀ x ∈ [ a , b ] f \in C[a,b]连续,则f在[a,b]有界。即存在常数M >0,使得|f(x)| \le M,\forall x \in [a,b] f∈C[a,b]连续,则f在[a,b]有界。即存在常数M>0,使得∣f(x)∣≤M,∀x∈[a,b]
半开区间则不一定成立,如:f(x)= 1 x \frac 1 x x1在区间(0,1]无上界。
性质二:最值定理
若 f ∈ C [ a , b ] f\in C[a,b] f∈C[a,b],则f在[a,b]上必定能取到最大(小)值。
开区间不一定成立。如果f(x)=x,在左开右开区间(0,1)没有最小值,也没有最大值。
不连续也不一定,如:
{ x x > 0 0.5 x = = 0 − x x < 0 \begin{cases} x && x >0 \\ 0.5 && x ==0 \\ -x && x <0 \\ \end{cases} ⎩
⎨
⎧x0.5−xx>0x==0x<0
在区间[-1,1]就没有最小值。
性质三:介质定理
若 f ∈ C [ a , b ] f\in C[a,b] f∈C[a,b],且f(a) ≠ \neq =f(b)。则对于任意介于f(a)和f(b)之间的数C,必定存在 c ∈ ( a , b ) , f ( c ) = C c\in(a,b),f(c)=C c∈(a,b),f(c)=C
推论(零点定理):即C=0。
单调且有界则必定有极限
数列{ x n x_n xn}满足 x 1 ∈ ( 0 , π ) , x n + 1 = sin x n , n ∈ Z + x1\in(0,\pi),x_{n+1}=\sin x_n,n\in Z+ x1∈(0,π),xn+1=sinxn,n∈Z+,求 lim x → ∞ x n \lim\limits_{x \to \infty}x_n x→∞limxn。
x 2 ⋯ + ∞ ∈ ( 0 , 1 ) x_{2\cdots +\infty} \in(0,1) x2⋯+∞∈(0,1) 即有下界。
x ∈ ( 0 , π ) , sin x < π x \in (0,\pi),\sin x < \pi x∈(0,π),sinx<π,即单调减少。
n → ∞ , x n + 1 = x n = 极限 , 即 x n = s i n x n ,即 x n = 0 n\to \infty,x_{n+1}=x_n=极限,即x_n = sin x_n,即x_n=0 n→∞,xn+1=xn=极限,即xn=sinxn,即xn=0
f(x)= x − sin x , f ( 0 ) = 0 f ( x ) ′ = 1 − cos x x - \sin x, f(0)=0 f(x)'=1-\cos x x−sinx,f(0)=0f(x)′=1−cosx,即f(x)单调增加,故0<x < π \pi π,x > sinx。
易错题
存在以下情况:f(x)在 x 0 x_0 x0的某去心邻域无界,但极限不是 ∞ \infty ∞(极限不存在)。如: f ( x ) = 1 ÷ sin 1 x , x → 0 f(x)=1 \div \sin \frac 1x,x \to 0 f(x)=1÷sinx1,x→0,时左右极限不存在。 x → 0 时 , 1 ÷ x → + ∞ , sin ( 1 ÷ x ) 在 [ − 1 , 1 ] 震荡,即在去心邻域内可能是 1 , − 1 , + ∞ , − ∞ x \to 0时,1 \div x \to +\infty,\sin (1 \div x)在[-1,1]震荡,即在去心邻域内可能是1,-1,+\infty,-\infty x→0时,1÷x→+∞,sin(1÷x)在[−1,1]震荡,即在去心邻域内可能是1,−1,+∞,−∞
扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容









所有评论(0)