学术诚信声明 

       本人郑重声明：本程序设计实验报告的所有内容均为本人独立完成，严格遵守学校学术诚信相关规定。报告中涉及的代码编写、错误分析、功能解析等内容，未抄袭、剽窃他人研究成果，未借用AI工具生成核心内容后直接套用，所有实验过程与结论均为真实的实操结果。若存在学术不端行为，本人自愿承担相应的责任与后果。

摘要

       数学无处不在，让我们一起体会数学的魅力。本文将通过一串代码来展现圆周率π的近似计算，介绍两种典型的计算方法：正多边形逼近法与随机数蒙特卡洛法。为了让人们更加了解π的近似计算，本文将从代码的核心逻辑分析开始，逐一拆解两种方法的实现思路，并呈现编译过程中遇到的问题及解决方法，进而展现最终运行成功的结果。希望这篇文章可以让每一个热爱数学的人对π的近似计算有更清晰的认识。

一 选题与准备

1.1 选题

在190个文件夹中，出于对圆周率的好奇，我选中了这个序号为80的文件夹。希望通过代码实现理解两种算法的数学原理与编程落地思路。

1.2 环境准备

（1）操作系统：Windows 11

（2）编译器：Dev-C++

（3）辅助工具：ChatGPT、CSDN社区、《C语言程序设计》教材、知网

二 编译调试过程

2.1 初始编译与错误分析

打开文件，代码出现在编译器上，首次编译出现了许多报错，核心错误原因如下：

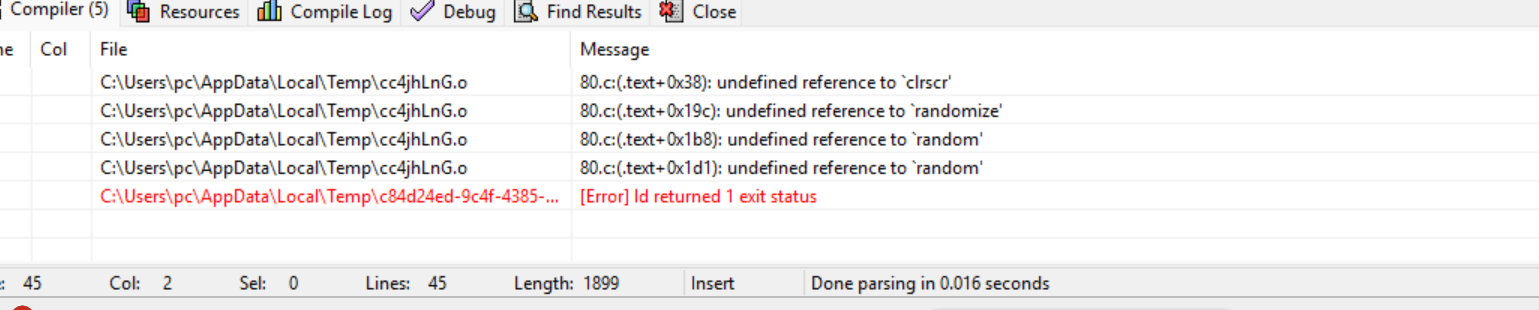
1.非标准库函数兼容问题

         (1)clrscr() 未定义。Dev-C++的标准库中没有clrscr()函数。

         (2)randomize ()未定义。现代C标准中需要用srand()/rand()替代。

         (3)getch()未定义。getch()属于<conio.h>头文件的函数。

2.编码与格式错误

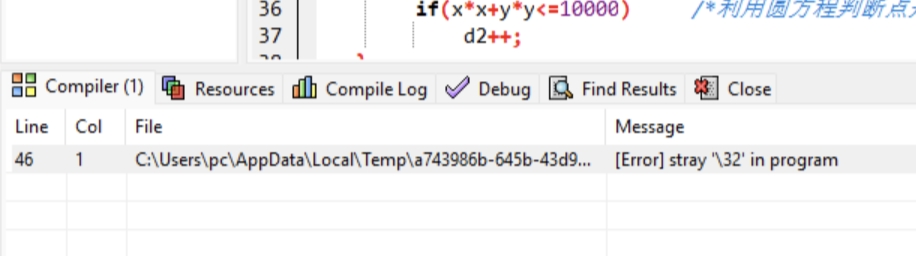
代码中存在隐藏的特殊字符，编译器无法识别。

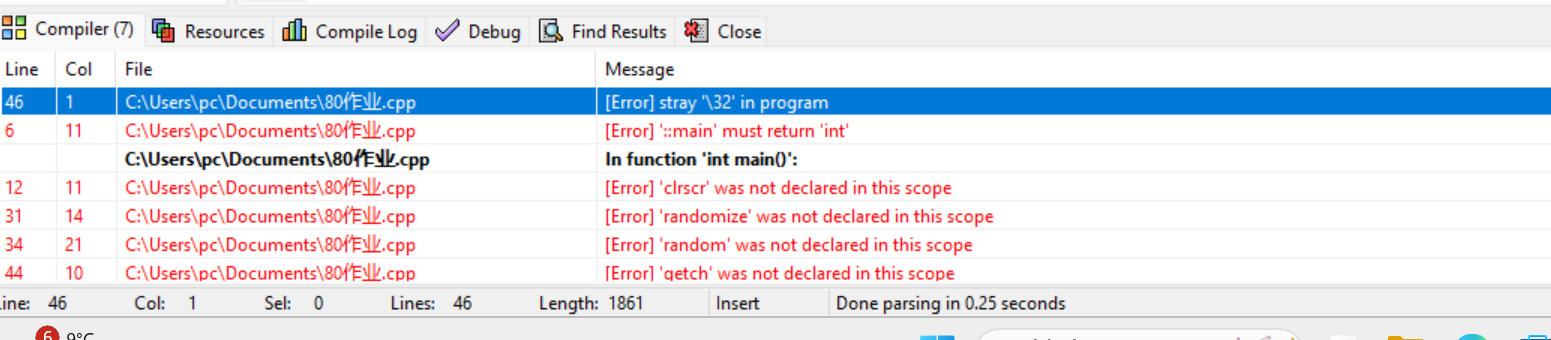
3.语法与标准合规问题

(1)void main()不符合C标准。C++要求main函数的返回值类型必须是int，void main()仅为部分旧编译器的非标准写法。

(2)浮点数比较逻辑不规范。代码中if (2*i*b-i*e<1e-15) 未用绝对值函数fabs（），直接比较浮点数差值易因精度误差导致判断失效。

2.2 错误修正

针对以上问题，我进行了修改，以下列举一些主要修改内容：

1.替换清屏函数：删除clrscr（）；

2.修正main函数：将void main（）改为int main（），并且在函数末尾添加return 0；

3.替换随机数函数：用rand（）%101替代random(101), 实现0-100的随机整数生成；

4.规范精度判断表达式：将if(2*i*b-i*e<1e-15)修改为if（fabs(2*i*b-i*e)<1e-5），并且引入<math.h>，用fabs计算浮点数绝对值；

5.修正grtch()：引入<conio.h>头文件。

2.3 反复调试

修正错误之后，得到以下运行结果：

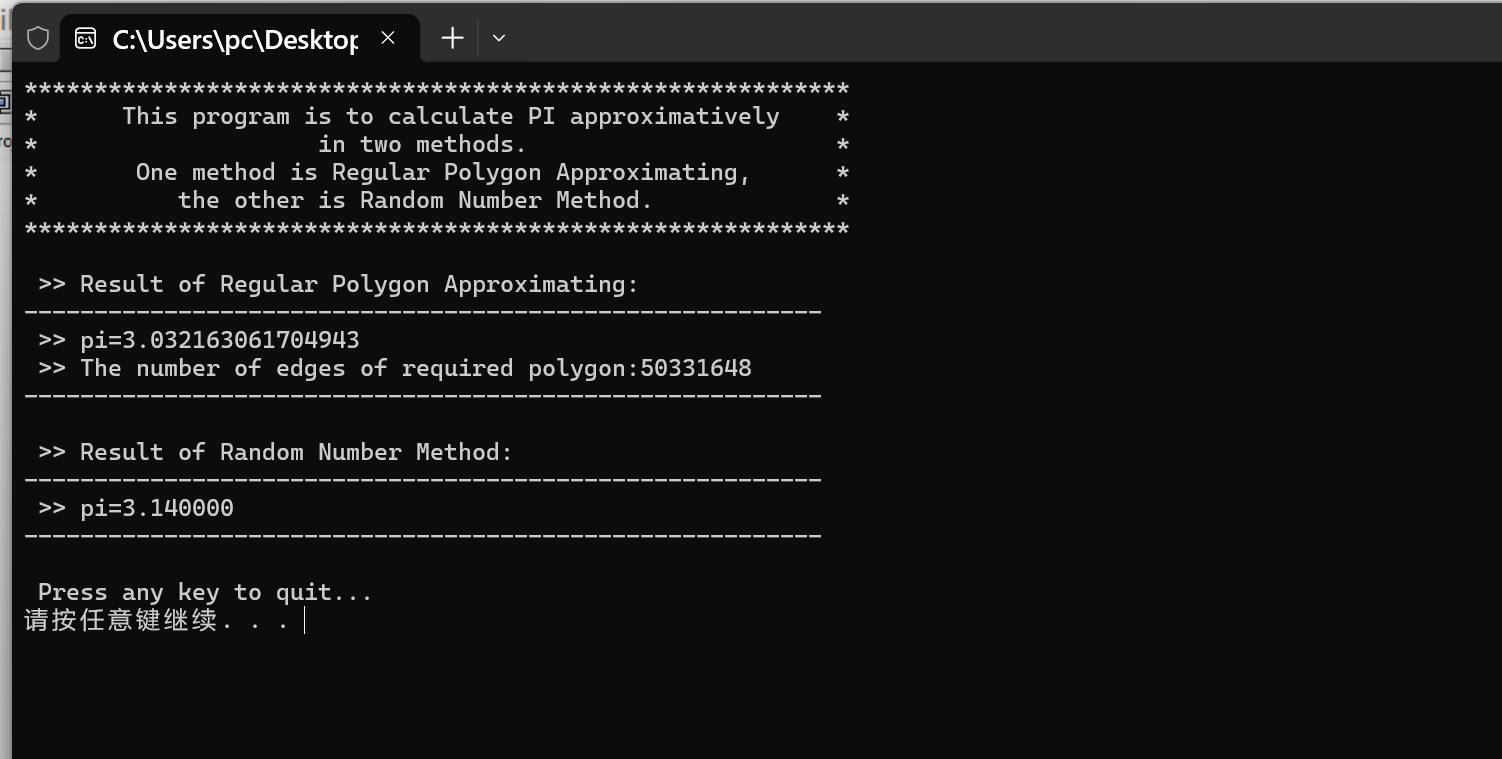
三 代码理解与重命名

3.1 运行测试

程序运行之后，首先是输出功能介绍，然后分两部分展示结果:

1. 正多边形逼近法：从正六边形（初始边数）开始，不断增加正多边形的边数，直到计算精度达到1e-15，输出最终的π近似值和对应的正多边形边数。

2. 随机数蒙特卡洛法：生成30000组0-100的随机坐标(x,y)，通过判断点是否落在以原点为圆心、半径100的圆内，利用“圆面积/正方形面积=π/4”的原理计算π值。

3.2 代码解析

1.正多边形逼近法核心逻辑

（1）数学原理：正多边形的边数越多，其周长越接近外接圆周长，通过周长=2πr推导π的近似值。

（2）代码中b存储正多边形的半边长，d计算边数翻倍后的半边长增量，通过循环迭代更新边数和半边长，直到精度满足要求。

2.蒙特卡洛法核心逻辑

（1）数学原理：在边长为2R的正方形内随机投点，落在半径为R的圆内的点的比例近似为πR*R/4R*R=π/4，因此π近似等于4*（圆内点数/ 总点数）。

（2）代码中c2统计总投点次数，d2统计圆内点次数，最终通过4.0*d2/N计算π的近似值。

3.3 重命名

基于程序的功能，我将其命名为“80-关于π的近似计算。

四 使用VSCode管理项目

4.1 VSCode环境配置

1.下载并安装VSCode，安装C/C++插件（Microsoft官方插件）。
2. 配置MinGW编译器路径，在VSCode的 settings.json 中设置编译器路径，确保 gcc / g++ 命令可在终端执行。
 
4.2 在VSCode中编译运行
 
1. 将代码保存为 pi_.keep.c 文件，打开VSCode终端。
2. 执行编译命令： gcc pi_.keep.c -o pi_.keep -lm （ -lm 链接数学库，支持 sqrt / fabs 等函数）。
3. 运行可执行文件： ./pi_.keep.exe （Windows环境），查看输出结果。

五 代码版本管理

5.1 Gitee仓库创建

在Gitee平台注册账号，创建一个仓库，用于存放本次项目的完整代码。

5.2 VSCode集成Git

1.初始化本地Git仓库

2.添加文件到暂存区

3.提交到本地仓库

4.关联远程仓库

5.推送到远程仓库

以上为基本步骤，详细操作可在哔哩哔哩网站进行查询。

六 总结

这是一次全新的经历，这让我的个人能力得到了提升。本项目通过C语言成功实现π的两种经典近似计算方法，过程中解决了非标准函数库兼容、数学公式编程转化等多个问题，它不仅加深了我对C语言语法规范、数值计算逻辑的理解，更让我体会到了“数学原理→代码实现→调试优化→版本管理”的完整编程闭环思路。人的知识是有限的，但学习的能力是无限的，我们要不断地探索，不断地提升自己的能力。希望通过本文你能尝试不同的方法来实现π的近似计算，并且对比不同方法的计算精度与运行效率。

附录

Gitee仓库链接：

https://gitee.com/long-xinting/course-report.git